2023年安徽省六安市舒城县五校联盟中考数学模拟试卷（含答案）

这是一份2023年安徽省六安市舒城县五校联盟中考数学模拟试卷（含答案），共24页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。

2023年中考舒城县五校联盟数学模拟试卷
温馨提示：数学试卷共七大题23小题，满分150分。考试时间共150分钟。
一、单选题（本大题10小题，每小题4分，满分40分）
1． 2023的相反数是（　　）
A． B． C． D．2023
2．春暖花开，城市按下快进键，天津地铁客流持续增长，2023年2月25日客运量达到1853000人次，截止当天该客运量创近3年新高．将1853000用科学记数法表示应为（　　）
A． B． C． D．
3．下列运算正确的是（　　）.
A． B． C． D．
4．休闲广场供游客休息的石板凳如图所示，它的俯视图是（　　）

A． B． C． D．
5．若点，，都在反比例函数的图象上，则，，的大小关系是（　　）
A． B． C． D．
6．下列分解因式正确的是（　　）
A． B．
C． D．
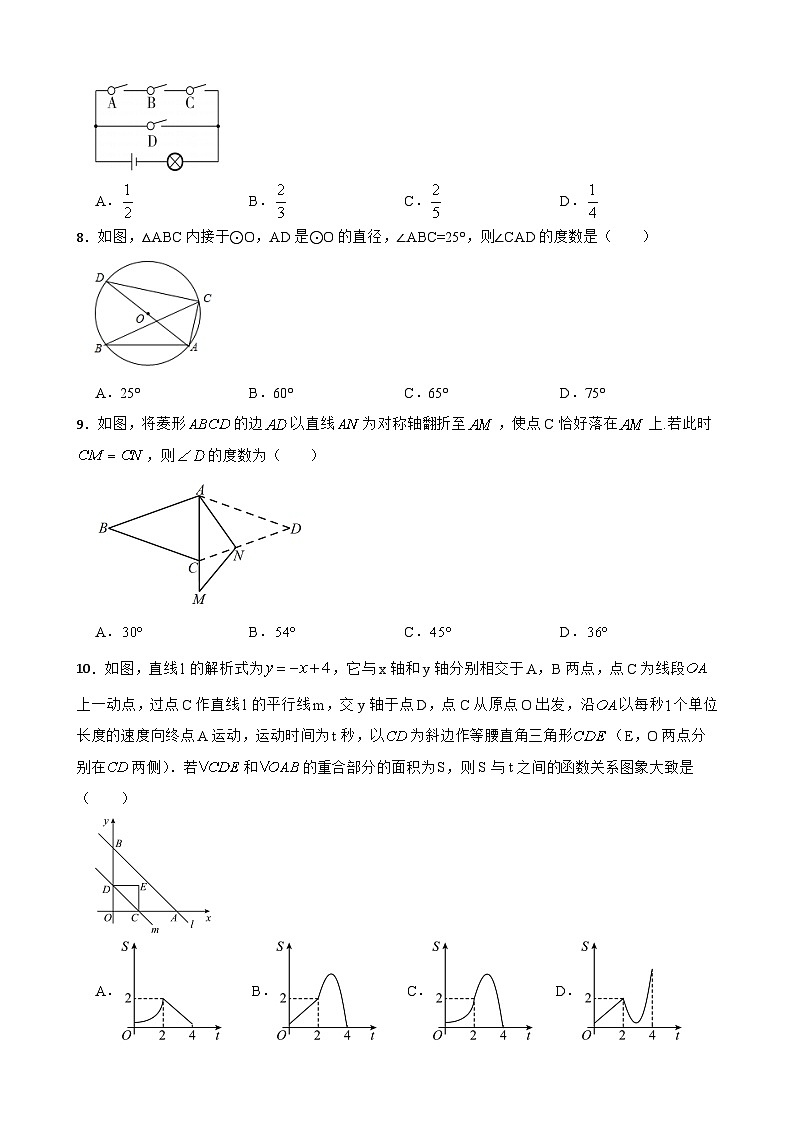
7．如图，电路图上有四个开关，，，和一个小灯泡，闭合开关或同时闭合开关，，都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（　　）

A． B． C． D．
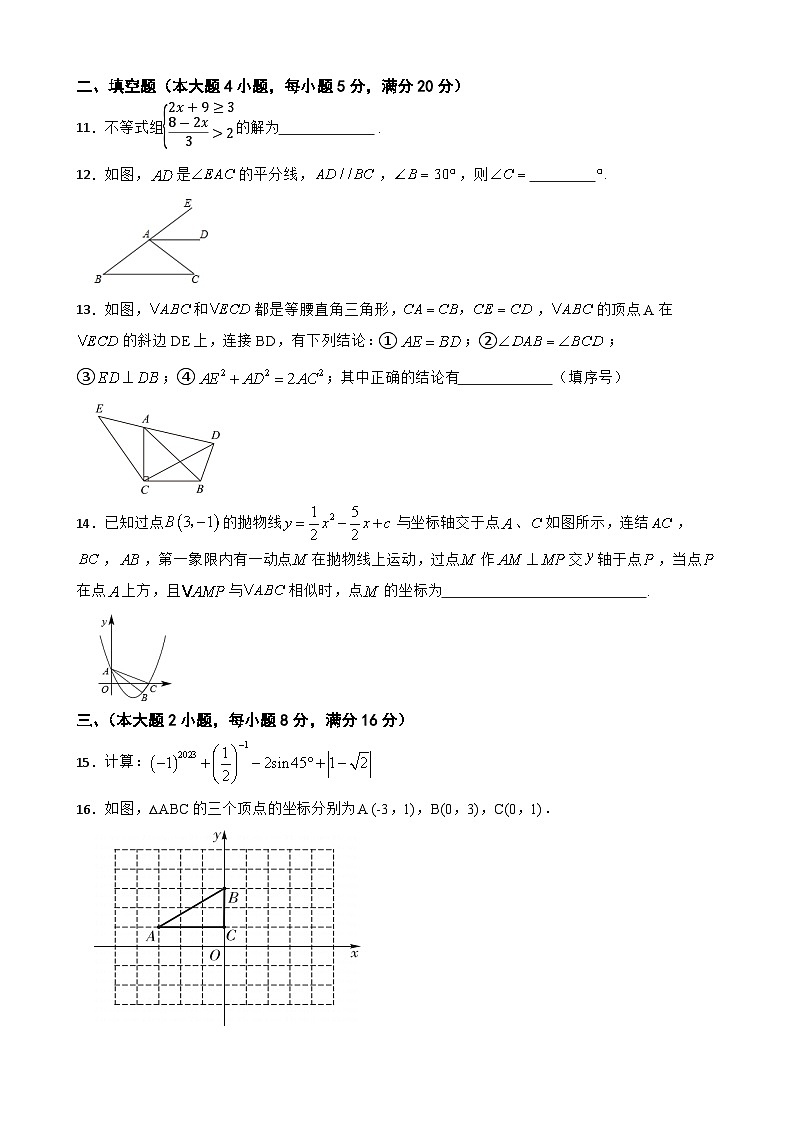
8．如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=25°，则∠CAD的度数是（　　）

A．25° B．60° C．65° D．75°
9．如图，将菱形的边以直线为对称轴翻折至，使点C恰好落在上.若此时，则的度数为（　　）

A． B． C． D．
10．如图，直线l的解析式为，它与x轴和y轴分别相交于A，B两点，点C为线段上一动点，过点C作直线l的平行线m，交y轴于点D，点C从原点O出发，沿以每秒个单位长度的速度向终点A运动，运动时间为t秒，以为斜边作等腰直角三角形（E，O两点分别在两侧）．若和的重合部分的面积为S，则S与t之间的函数关系图象大致是（　　）

A． B． C． D．
二、填空题（本大题4小题，每小题5分，满分20分）
11．不等式组2x+9≥38-2x3>2的解为　 　 .
12．如图，是的平分线，，，则　 　

13．如图，和都是等腰直角三角形，，的顶点A在的斜边DE上，连接BD，有下列结论：①；②；③；④；其中正确的结论有　 　（填序号）

14．已知过点的抛物线与坐标轴交于点、如图所示，连结，，，第一象限内有一动点在抛物线上运动，过点作交轴于点，当点在点上方，且与相似时，点的坐标为　 　.

三、（本大题2小题，每小题8分，满分16分）
15．计算：
16．如图，△ABC的三个顶点的坐标分别为A (-3，1)，B(0，3)，C(0，1)．

⑴将△ABC向下平移3个单位长度，得△A'B'C，画出△A'B'C；
⑵写出点B'的坐标：
⑶将△ABC以点C为旋转中心顺时针旋转90°，得△A"B"C，画出△A"B"C．
四，（本大题2小题，每小题8分，满分16分）
17．某校英语考试采取网上阅卷的形式，已知该校甲、乙两名教师各阅卷张，甲教师的阅卷速度是乙教师的2倍，结果甲教师比乙教师提前2个小时完成阅卷工作．求甲、乙两名教师每小时批阅学生试卷的张数．
18．用棋子摆出下列一组图形：

（1）填写下表：
图形编号
1
2
3
4
5
6
图形中的棋子
6
　
　
　
　
　
（2）照这样的方式摆下去，写出摆第 n 个图形棋子的枚数；
（3）如果某一图形共有99枚棋子，你知道它是第几个图形吗？
五、（本大题2小题，每小题10分，满分20分）
19．如图，从点D处观测楼房的楼顶端点B的仰角为，从点D处沿着直线直走到达点E，从点E处观测楼顶端点B的仰角为，观测广告牌端点C的仰角为，求楼房的高度和广告牌的高度（结果精确到；参考数据：，，，，，，，，）.

20．如图，已知，以为直径，O为圆心的半圆交于点F，点E为弧的中点，连接交于点M，为的角平分线，且，垂足为点H.

（1）求证：是的切线；
（2）若，，求的长.
六、（本大题2小题，每小题12分，满分24分）
21．在“4·23世界读书日”来临之际，某学校开展“让阅读成为习惯”的读书活动，为了解学生的参与程度，从全校随机抽取a名学生进行问卷调查，获取了每人平均每天阅读时间t（单位：分钟），将收集的数据分为A，B，C，D，E五个等级，绘制成如下不完整放计图表.
平均每天阅读时间统计表
等级
人数

5

10

b

80

c

请根据图表中的信息，解答下列问题：
（1）直接写出a，b的值；
（2）这组数据的中位数所在的等级是　 　；
（3）学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”，若该校学生以2000人计算，估计可评为“阅读达人”的学生人数.
22．如图，在△ABC中，∠BCA=90°，BC=8，AC=6，点D是AB边上的中点，点E是BC边上的一个动点，连接DE，将△BDE沿DE翻折得到△FDE．

（1）如图①，线段DF与线段BC相交于点G，当BE=2时，则　 　；
（2）如图②，当点E与点C重合时，线段EF与线段AB相交于点P，求DP的长；
（3）如图③，连接CD，线段EF与线段CD相交于点M，当△DFM为直角三角形时，求BE的长．
七、单选题（本题满分14分）
23．抛物线（a，b，c是常数，）的顶点为D，与x轴相交于点，是y轴上的一个定点．
（1）若，且抛物线过定点M，求抛物线解析式和顶点D的坐标；
（2）已知抛物线的顶点D在x轴上方，且点D在直线上．
①若，求抛物线解析式和顶点D的坐标；
②若点E是直线上的动点，点F是x轴上的动点，当的周长的最小值时，直接写出抛物线的顶点D的坐标．

答案解析部分
1．【答案】C
【解析】【解答】解：2023的相反数是，
故答案为：C.
【分析】根据只有符号不同的两个数互为相反数解答即可.
2．【答案】B
【解析】【解答】；
故答案为：B．

【分析】利用科学记数法的定义及书写要求求解即可。
3．【答案】C
【解析】【解答】解：，，，故答案为：C.
【分析】A、根据同底数幂的乘法法则“同底数幂相乘，底数不变，指数相加”可得原式=a5；
B、根据同类项定义"同类项是指所含字母相同，且相同的字母的指数也相同的项"可知a2和a不是同类项，所以不能合并；
C、根据幂的乘方法则“幂的乘方，底数不变，指数相乘”可得原式=a6；
D、根据同底数幂的除法法则“同底数幂相除，底数不变，指数相减”可得原式=a2.

4．【答案】D
【解析】【解答】解：从上面看，可得俯视图为：

故答案为：D．

【分析】利用三视图的定义求解即可。
5．【答案】D
【解析】【解答】解：把代入反比例函数得，
把代入反比例函数得，
把代入反比例函数得，
，
故答案为：D．
【分析】利用反比例函数的性质求解即可。
6．【答案】D
【解析】【解答】解：A、，不符合题意；
B、，不符合题意；
C、，不符合题意；
D、，符合题意；
故答案为：D．
【分析】利用完全平方公式，提公因式法分解因式求解即可。
7．【答案】A
【解析】【解答】解：画树状图得：

∵共有12种等可能的结果，现任意闭合其中两个开关，则小灯泡发光的有6种情况，
∴小灯泡发光的概率为：.
故答案为：A．

【分析】先利用树状图求出所有等可能的情况数，再利用概率公式求解即可。
8．【答案】C
【解析】【解答】解：∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠D=∠ABC=25°，
∴∠CAD=90°﹣∠D=65°.
故答案为：C.
【分析】由圆周角定理可得∠ACD=90°，∠D=∠ABC=25°，然后根据∠CAD=90°-∠D进行计算.
9．【答案】D
【解析】【解答】解：∵四边形为菱形，
∴，
∴，
根据折叠可知，，
∵，
∴，
∵，
∴，
∴，
∵，
∴，
即，
∴.
故答案为：D.
【分析】由菱形的性质可得AD=CD，根据等腰三角形的性质可得∠ACD=∠CAD，根据折叠可知∠M=∠D，由等腰三角形的性质以及外角的性质可得∠ACD=∠CAD=2∠D，然后利用内角和定理进行计算.
10．【答案】C
【解析】【解答】解：如图：
∵直线，它与x轴和y轴分别相交于A，B两点，
∴，
∵点C从原点O出发，沿以每秒个单位长度的速度向终点A运动，运动时间为t秒，

∴，，
∴，
∴，
∴，，
∴，
∵，
∴，
当，；
∴当，；当，．
故答案为：C．

【分析】根据直线，它与x轴和y轴分别相交于A，B两点，得出，根据点C从原点O出发，沿以每秒个单位长度的速度向终点A运动，运动时间为t秒，得出，，点E、F的坐标，根据，得出，当，；当，；当，，即可得出答案。
11．【答案】-3≤x＜1
【解析】【解答】解：，
解不等式①得：，
解不等式②得：，
不等式组的解集为：
故答案为：-3≤x＜1.
【分析】首先分别求出两个不等式的解集，然后取其公共部分即为不等式组的解集.
12．【答案】30
【解析】【解答】解：，

，，
又平分，
，
，
故答案为：30.
【分析】对图形进行角标注，根据平行线的性质可得∠1=∠B，∠2=∠C，根据角平分线的概念可得∠1=∠2，则∠B=∠C，据此解答.
13．【答案】①②③④
【解析】【解答】解：∵和都是等腰直角三角形，
∴，
∴，即：，
∵，
∴，
∴，故①正确；
由三角形外角定理，，
∵，
∴，
∵，
∴，
∵，
∴，故②正确；
∵，
∴，
∵，
∴，
即：，故③正确；
∵，
∴在中，，
∵为等腰直角三角形，
∴，
∴，
∵，
∴，故④正确；
故答案为：①②③④.
【分析】由等腰直角三角形的性质可得∠ECD=∠ACB，结合角的和差关系可得∠ECA=∠DCB，利用SAS证明△ACE≌△BCD，据此判断①；由三角形外角定理可得∠DAC=∠E+∠ECA，由角的和差关系可得∠DAC=∠DAB+∠BAC，进而推出∠ECA=∠DAB，由①可得∠ECA=∠DCB，进而可判断②；根据全等三角形的性质可得∠E=∠CDB=45°，然后根据∠BDE=∠CDA+∠CDB求出∠BDE的度数，进而判断③；由勾股定理可得AD2+BD2=AB2，根据等腰直角三角形的性质以及勾股定理可得AB2=2AC2，则AD2+BD2=2AC2，结合AE=BD可判断④.
14．【答案】（11，35）或
【解析】【解答】解：把点代入，得：
，
∴，
∴抛物线的解析式为，
令，得，
∴，
令，则，
解得，
∴，
∴，
∵
∴，，
∴，
∴为直角三角形，且，
过点M作轴于G，则，

设点M的横坐标为x，由M在y轴右侧可得，则，
∵，
∴，
如图，当时，则，
∴，
∴，
同理可得，，
∴，
∴，则，
把代入，得
，解得： 或0（舍去），
∴；
∴，
∴，
同理可得，，
则，
把代入，得：
，解得：或0（舍去），
∴，
综上，点M的坐标为（11，35）或.
故答案为：（11，35）或.
【分析】将点B的坐标代入求出c的值，从而可得抛物线的解析式，分别令解析式中x=0与y=0算出对应的y与x的值，从而可得A、C的坐标，利用两点间的距离公式算出AC、BC、AB，根据勾股定理的逆定理判断出△ABC是直角三角形，过点M作MG⊥y轴于G，则∠MGA=90°，设点M的横坐标为x，由M在y轴右侧可得x＞0，则MG=x，当∠MAP=∠ACB时，△MAP∽△BCA，根据相似三角形对应边成比例得，同理△AGM∽△AMP，，从而用含x的式子表示出点M的坐标，将点M的坐标代入抛物线的解析式算出x的值，可得点M的坐标；当∠MAP=∠CAB时，△MAP∽△BAC，根据相似三角形对应边成比例得，同理AG=3MG=3x，从而用含x的式子表示出点M的坐标，将点M的坐标代入抛物线的解析式算出x的值，可得点M的坐标，综上即可得出答案.
15．【答案】解：


.
【解析】【分析】根据有理数的乘方法则、负整数指数幂的运算性质、特殊角的三角函数值以及绝对值的性质可得原式=-1+2-2×+-1，然后计算乘法，再根据二次根式的加法法则以及有理数的加减法法则进行计算.
16．【答案】解：⑴如图所示，△A'B'C'即为所求．

⑵由图知，点B'坐标为(0，0) ；
⑶如图所示，△A"B"C即为所求．
【解析】【分析】（1）将三个顶点分别向下平移3个单位，再首尾顺次连接即可；
（2）由所作图形即可得出答案；
（3）将点A、B分别绕点C顺时针旋转90° 得到其对应点，再与点C首尾顺次连接即可
17．【答案】解：设乙教师的阅卷速度是每小时张，甲教师的阅卷速度是每小时张，
根据题意可得：，
，
经检验，是原分式方程的解，
∴，
答：甲教师的阅卷速度是每小时张，乙教师的阅卷速度是每小时张．
【解析】【分析】设乙教师的阅卷速度是每小时张，甲教师的阅卷速度是每小时张，根据题意列出方程，再求解即可。
18．【答案】（1）解：填写下表：
图形编号
1
2
3
4
5
6
图形中的棋子
6
9
12
15
18
21
（2）解：第 个图形棋子的枚数是 个
（3）解：由题意得， ，
解得 ，
答：如果某一图形共有99枚棋子，它是第 个图形
【解析】【分析】解题注意根据图形发现规律，并用字母表示．然后根据条件代入计算．（1）观察图形，发现（1）中是6个棋子．后边依次多3个棋子．根据这一规律即可解决问题；（2）根据（1）中规律解答即可；（3）根据题意列出方程，求出n的值即可．
19．【答案】解：由题意，得，，
设，则，.
，
∴，
解得.
∴，.
又∵，
∴.
∴.
答：楼房的高度为，广告牌的高度为.
【解析】【分析】 设 ，根据tan∠ADB=，求出AB=1.96x，继而求出，根据列出关于x方程并解之，可得AB、AE的长，利用解直角三角形求出AC的长，利用BC=AC-AB即可求解.
20．【答案】（1）证明：连接，

于H，，

，
，
又为的中点，
，
是直径，
，
，
又，
，
，
，
又是直径，
是半圆O的切线；
（2）解：，，
由（1）知，，

在中，于H，平分，
，

，为公共角，
，
得，
.
在中，根据勾股定理得.
【解析】【分析】（1）连接EC，根据题意结合内角和定理可得∠3=∠4，由对顶角的性质可得∠4=∠5，则∠3=∠4=∠5，由圆周角定理可得∠6=∠7，∠E=90°，则∠5+∠6=90°，由平行线的性质可得∠2=∠6=∠1，则∠3+∠7=90°，据此证明；
（2）利用勾股定理可得AC的值，由角平分线的性质可得AM=AB=3，则CM=2，由两角对应相等的两个三角形相似可得△CME∽△BCE，根据相似三角形的性质可得EB=2EC，然后利用勾股定理进行计算.
21．【答案】（1）解：，
（2）D等级
（3）解：∵统计表中平均每天阅读时间不低于50分钟的学生人数为65人，
∴E级的比例为：，
当总人数为2000人时，可评为“阅读达人”的学生人数为：人
【解析】【解答】解：（1）∵D级的人数为80人，占比为40%，
∴，
∴，
∵C级人数的占比为20%，
∴.
∴，；
（2）∵，
根据题意，中位数应是第100个、第101个数据的平均数，且第100个数据在D等级，第101个数据在D等级，它们的平均数也在D等级，
故答案为：D等级.
【分析】（1）利用D人数所占的比例乘以总人数=对应的人数可求出a的值，根据C所占的比例乘以总人数可得b的值；
（2）根据总人数可求出c的值，中位数是第100个、第101个数据的平均数，且第100个数据在D等级，第101个数据在D等级，据此可得中位数所在的等级；
（3）利用平均每天阅读时间不低于50分钟的学生人数除以抽取的人数，然后乘以2000即可.
22．【答案】（1）
（2）解：∵∠PCD=∠BCD，∠BCD=∠B，
∴∠PCD=∠B，
∵∠CPD=∠BPC，
∴△CPD∽△BPC，
∴，
设DP=5k，CP=8k，
∵CP2=PD•PB，
∴64k2=5k（5k+5），
∴k=，
∴PD=5k=
（3）解：①如图③-a，

当∠FMD=90°时，
∵∠F=∠B，∠FMD=∠ACB=90°，
∴△FDM∽△BAC，
∴，
∴，
∴DM=3，
∴CM=CD-DM=2，
∵∠ECM=∠B，
∴∠CME=∠ACB=90°，
∴△CEM∽△BAC，
∴，
∴，
∴CE=，
∴BE=；
如图③b，

当∠FDM=90°时，
∵∠F=∠BCD，∠FMD=∠CME，
∴∠CEM=∠FDM=90°，
∴∠FED=∠BED=45°，
作DH⊥BC于H，
则△BDH∽△BAC，
∴，
∴，
∴DH=3，BH=4，
∴EH=DH=3，
∴BE=3+4=7．
综上所述，BE=或7．
【解析】【解答】（1）解：连接CD，

∵在△ABC中，∠BCA=90°，BC=8，AC=6，
∴AB==10，
∵点D是AB边上的中点，
∴CD=BD=AB=5，
∴∠DCB=∠B，
∵将△BDE沿DE翻折得到△FDE，
∴∠F=∠B，EF=EB=2，
∵∠CGD=∠FGE，
∴△CDG∽△FEG，
∴，
故答案为：；

【分析】（1）连接CD，由勾股定理求出AB=10，由直角三角形斜边中线的性质可得CD=BD=AB=5，利用等边对等角可得∠DCB=∠B，由折叠可得∠F=∠B，EF=EB=2，证△CDG∽△FEG，利用相似三角形的性质即可求解；
（2）证明△CPD∽△BPC，可得，即得CP2=PD•PB， 设DP=5k，CP=8k，代入等式求出k值，即可求解；
（3）分两种情况：①当∠FMD=90°时，②当∠FDM=90°时， 根据相似三角形的判定与性质分别求解即可.

23．【答案】（1）解：当，且抛物线过定点时，，
把，代入其中，可得：4a-6+c=0c=4，解得：a=12c=4，
∴，
∵，
∴顶点的坐标为；
（2）解：①由点D在直线上，设，
∵，
由两点之间距离公式可得：，
解得：，则，
∴，
则设抛物线解析式为：，代入，
可得：，解得：，
∴抛物线解析式为：；
②作点分别关于直线，轴的对称点，，连接，，，
则，，
∴的周长，当，，，在同乙直线上时取等号；

即：的周长的最小值为，亦即，
连接点与对称点、，交对称轴于，轴于，过点作，交于，过点作，
由可知，当时，，即：，
由题意可知，，则，，为等腰直角三角形，
∴，，
则，
∴，
则由轴对称可知，，轴，且，，
则为等腰直角三角形，，，
设，则，，
，即，
∵，
∴，
又∵，
∴，即：，，
∴，，
∴，
由勾股定理可得：，
即：，整理得：，
解得：（负值舍去），
∴，则，
∴，
∴点的坐标为．
【解析】【分析】（1）利用待定系数法求出函数解析式，再利用配方法求出点D的坐标即可；
（2）①先求出点D的坐标，再求出函数解析式即可；
②作点分别关于直线，轴的对称点，，连接，，，则，，的周长，当，，，在同乙直线上时取等号，再画出图象并求解即可。