2023年浙江省温州瓯海区联盟学校中考数学冲刺卷+（对标温州中考）（含答案）

这是一份2023年浙江省温州瓯海区联盟学校中考数学冲刺卷+（对标温州中考）（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
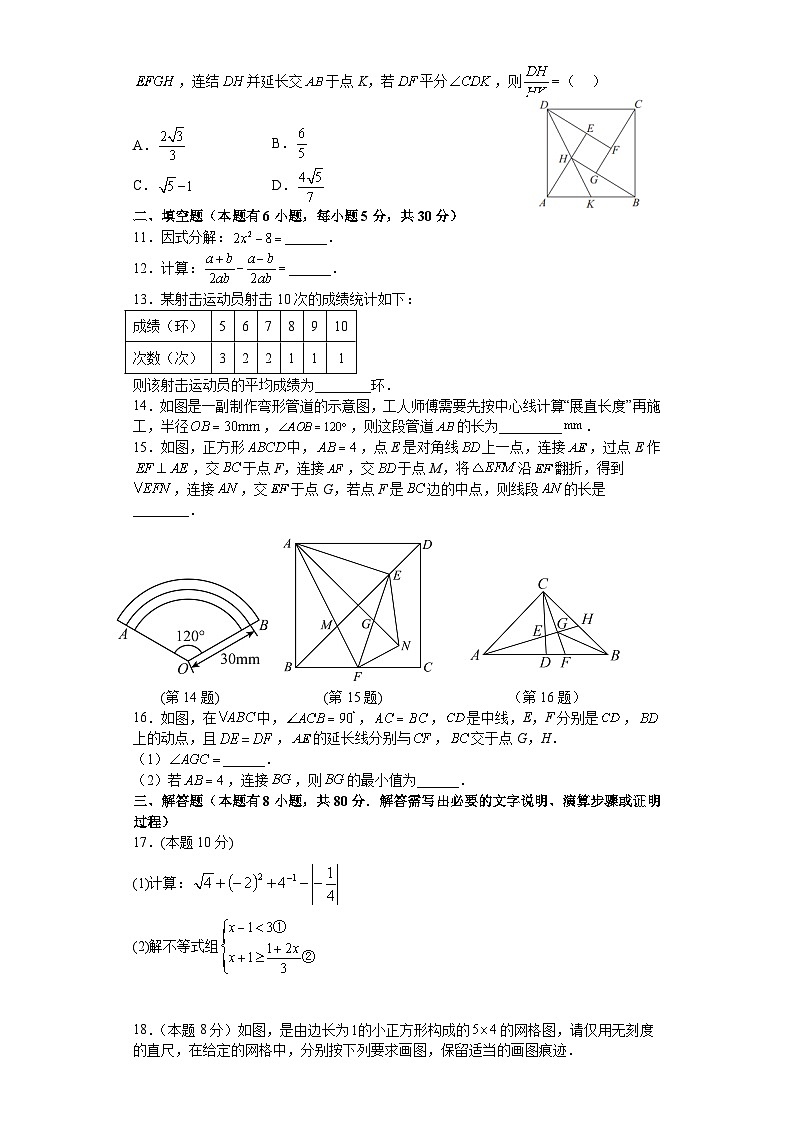
2023年温州瓯海区联盟学校中考数学冲刺卷（对标温州中考）一、选择题（本题10小题，每题4分，共40分）1．计算的结果等于（    ）A． B． C． D．2．如图所示的几何体，其俯视图是（    ）A． B． C．D．3．某校九年级学生视力情况的统计图如图所示．若九年级近视的学生人数有300名，则九年级学生视力正常的有（   ）A．50名 B．150名 C．300名 D．500名   4．下列运算正确的是（    ）A．a2.a3=a6 B．a5+a5=a10 C．a6÷a2=a3 D．（a3）2=a65．从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动，则甲与乙恰好被选中的概率是（　　）A． B． C． D．6．关于x的一元二次方程 有两个相等的实数根，k的取值为（     ）A．            B．               C．            D．k=17．如图，在中，AB是的直径，，，则的度数为（   ） A． B． C． D．8．已知点，在二次函数的图象上，若，则下列结论正确的是（    ）A． B． C． D．9．设函数，，直线的图象与函数，的图象分别交于点，，得（    ）A．若，则 B．若，则C．若，则 D．着，则10．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形与正方形，连结并延长交于点K，若平分，则（    ） A． B． C． D．二、填空题（本题有6小题，每小题5分，共30分）11．因式分解：______．12．计算：______．13．某射击运动员射击10次的成绩统计如下：成绩（环）5678910次数（次）322111则该射击运动员的平均成绩为________环．14．如图是一副制作弯形管道的示意图，工人师傅需要先按中心线计算“展直长度”再施工，半径，，则这段管道的长为_________．15．如图，正方形中，，点E是对角线上一点，连接，过点E作，交于点F，连接，交于点M，将沿翻折，得到，连接，交于点G，若点F是边的中点，则线段的长是________．        (第14题)               (第15题)                  （第16题）16．如图，在中，，，是中线，E，F分别是，上的动点，且，的延长线分别与，交于点G，H．（1）______．（2）若，连接，则的最小值为______．三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17．(本题10分)(1)计算：(2)解不等式组  18．（本题8分）如图，是由边长为的小正方形构成的的网格图，请仅用无刻度的直尺，在给定的网格中，分别按下列要求画图，保留适当的画图痕迹．(1)在图中画一个平行四边形，要求一条边长为且面积为；(2)在图中画一个矩形，要求一条边长为且面积为．19．（本题8分）学校为了解九年级学生中考体育成绩的情况，从九年级学生中随机抽取男生、女生各10名学生进行考前检测，这些学生的成绩记为（成绩为整数，单位：分，满分为60分），将所得的数据分为4个等次：A等：；等：；等：；等：．学校对数据进行分析后，得到了如下部分信息：男生成绩在这一组的数据是：46，44，44，48；男生成绩的频数统计表等次频数频率等30.3等4——等——等10.1女生成绩是：42，60，39，56，52，39，55，39，42，56；抽取的男生和女生中考体育测试成绩的平均数、中位数、众数如下表： 平均数中位数众数男生4844女生47请根据以上信息解答下列问题：(1)______；______；______；(2)请选取一个统计量对该校九年级男生与女生的中考体育测试成绩进行评价，并说明理由；(3)若该校九年级共有680名学生，请估计这次中考体育测试成绩为A等次的人数．          20．（本题8分）如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E．(1)过点E作EFBC交AB于点F，求证：FB=FE．(2)若∠C=36°，求∠BAD的度数；     21．（本题10分）已知反比例函数的图象的左支如图6-3所示，它经过点B（-3，2）．（1）求这个反比例函数的表达式．补画这个反比例函数图象的另一支．（2）当y≤4，且时，求自变量x的取值范围． 22．（本题10分）如图，在△ABC中，O是AC上的一点，延长BO至D,使BO=OD,连结AD、CD(1)当AD//BC时， 求证：四边形是平行四边形.(2)过O作OE⊥BD交BC于E，连结DE,若BD=16，AD=12,，求CE的长．            23．（本题12分）如何确定隧道中警示灯带的安装方案？素材1 2022年10月，温州市府东路过江通道工程正式开工，建成后将成为温州瓯江第一条超大直径江底行车隧道．隧道顶部横截面可视为抛物线，如图1，隧道底部宽为，高OC为．   素材2货车司机长时间在隧道内行车容易疲劳驾驶，为了安全，拟在隧道顶部安装上下长度为的警示灯带，沿抛物线安装．（如图2）．为了实效，相邻两条灯带的水平间距均为（灯带宽度可忽略）;普通货车的高度大约为（载货后高度），货车顶部与警示灯带底部的距离应不少于．灯带安装好后成轴对称分布．问题解决任务1确定隧道形状在图1中建立合适的直角坐标系，求抛物线的函数表达式．任务2探究安装范围在你建立的坐标系中，在安全的前提下，确定灯带安装点的横、纵坐标的取值范围．任务3拟定设计方案求出同一个横截面下，最多能安装几条灯带，并根据你所建立的坐标系，求出最右边一条灯带安装点的横坐标．        24．（本题14分）如图，点在线段上，，点是线段上一动点，以为边向下方作正方形，以为腰向下方作等腰直角三角形，，当时，．(1)如下表，某同学分别用特殊值法和一般法求的长，请你将解答过程补充完整．探究1假设，求的长．探究2设，求的长．解：…解：…(2)过点，，的交边于点．①连结，，若是等腰三角形，求的长；②当与边有两个交点时，求的取值范围．
参考答案一、选择题1．A2．A3．B4．D5．C6．D7．B8．D9．C10．C二、填空题11．12．13．6.814．15．16．           三、解答题17．（1）6（2）解不等式①，得，，解不等式②，去分母得，移项，合并同类项得，故不等式组的解集为：．18.（1）解：画出边长为，高为的平行四边形，另一组边为，下图即为所求：（2）画出一组边长为，另一组边长为的矩形，下图即为所求：19．（1）解：∵女生成绩是：42，60，39，56，52，39，55，39，42，56，∴平均数；由男生成绩的频数统计表可得：A等人数有3人，B等人数有4人，男生成绩在这一组的数据是：46，44，44，48，∴中位数；由男生成绩的频数统计表可得：C等人数有2人，∴频率；（2）解：本题答案不唯一，如：因为男生与女生的平均数相等，所以在中考体育测试中男生与女生的成绩相当；因为女生的中位数大于男生的中位数，所以在中考体育测试中女生的成绩较好；（3）解：（人）答：估计这次中考体育测试成绩为A等次的人数为272人．20．（1）解:(1)∵AB=AC，∴∠C=∠ABC．∵∠C=36°，∴∠ABC=36°．∵AB=AC，D为BC的中点，∴AD⊥BC，∴∠BDA=90°．∴∠BAD=90°-∠ABC=90°-36°=54°．（2）(2)∵BE平分∠ABC，∴∠ABE=∠EBC．又∵EF∥BC，∴∠EBC=∠BEF．∴∠EBF=∠FEB．∴BF=EF． 21（1）将图象上点B的横坐标-3，纵坐标2分别代入表达式，得，解得k=-6．所以所求的反比例函数的表达式是．在已知图象上分别取一些点作出它们关于原点中心对称的点，然后用光滑曲线把它们依次连结，这样就得到反比例函数的图象中的另一分支．（2）x≤-1.5或x＞022.（1）证明略（2）223．解：【任务1】以拱顶为原点，建立如图1所示的直角坐标系，则顶点为，且过点B，设抛物线的解析式为：，把点代入得：，∴，∴抛物线的函数表达式为：；【任务2】∵普通货车的高度大约为，灯带底部距离货车顶部不小于，灯带长，∴当安装点的纵坐标，即安装点的纵坐标的最小值是，当时，，∴，∴安装点的横坐标的取值范围是：；【任务3】如图2，∵若顶点一侧悬挂5条灯带时，，若顶点一侧悬挂4条灯带时，，∴顶点一侧最多悬挂4条灯带，∵灯带挂满后成轴对称分布，∴共可挂8条灯带，∴最右边一条灯带的横坐标为：．24．（1）解：探究1：∵，∴，∵四边形是正方形，∴，又∵，∴，∴，∴是等腰直角三角形∴∴；探究2：∵，∴，∵四边形是正方形，，∴，∵是等腰直角三角形，∴．（2）解：①a.如图：当时， ，∴，∵，∴，∴四边形是矩形，∴，∴；b.当，,作，，∴，∵，∴，∴；②当点D圆上时，连结，设，则，由（1）可得：,则∴，∵正方形∴∴∵四边形是圆O的内接四边形∴∴∴∵∴，∴，即，解得：（舍弃），当与边相切于点 H，连结，作 ，交于点R，作,易知，设，则，∴，由得 ，解得：，综上，．