陕西省西安市周至县2023届高三三模文科数学试题（含答案）

这是一份陕西省西安市周至县2023届高三三模文科数学试题（含答案），共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
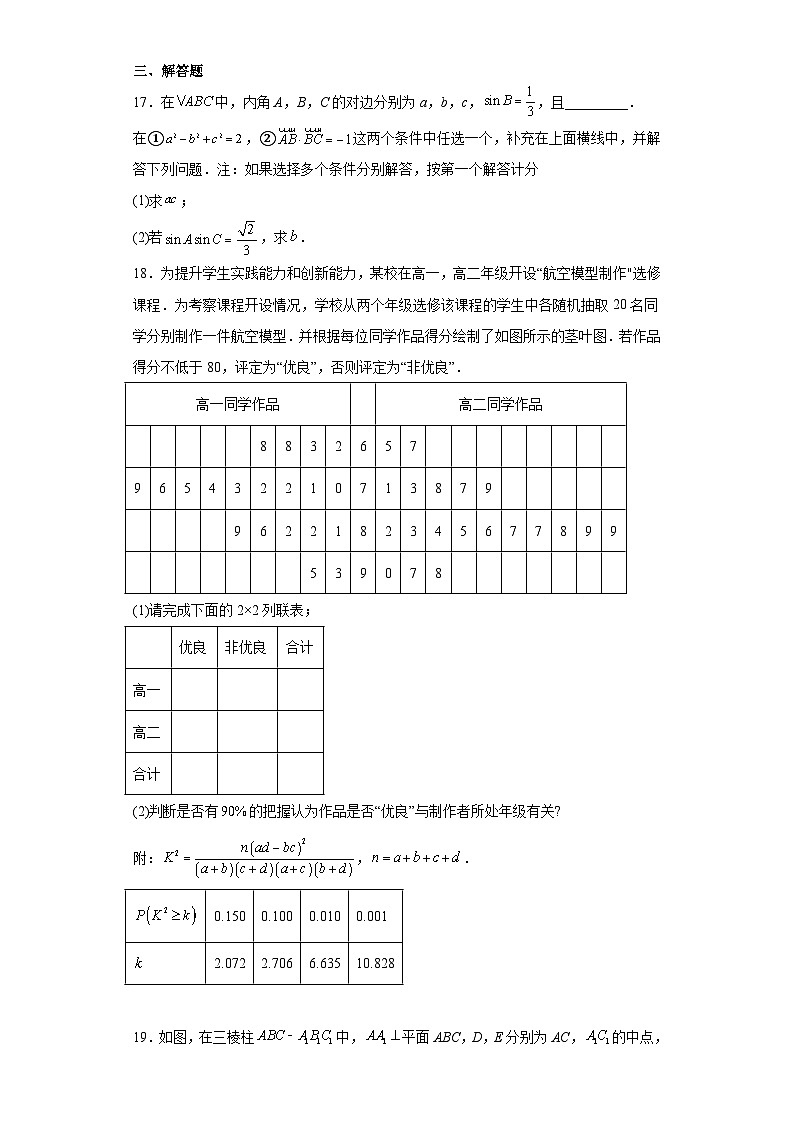
陕西省西安市周至县2023届高三三模文科数学试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．设全集，，（    ）A． B． C． D．2．在下列统计量中，用来描述一组数据离散程度的量是（    ）A．平均数 B．众数 C．中位数 D．标准差3．复数满足，则（    ）A． B． C． D．4．已知函数，则（    ）A．2 B．-2 C． D．-5．已知等比数列的公比，前3项和为，且，则（    ）A． B． C． D．6．如图是下列四个函数中的某个函数在区间上的大致图象，则该函数是（    ）A． B．C． D．7．“”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件8．已知椭圆：的左，右焦点分别为，，若椭圆上一点Р到焦点的最大距离为7，最小距离为3，则椭圆C的离心率为（    ）A． B． C． D．9．羽毛球单打实行“三局两胜”制（无平局）．甲乙两人争夺比赛的冠军．甲在每局比赛中获胜的概率均为，且每局比赛结果相互独立，则在甲获得冠军的条件下，比赛进行了三局的概率为（    ）A． B． C． D．10．设，是两条不同的直线，，，是三个不同的平面，下列说法正确的是（　　）A．若，，则 B．若，，则C．若，，则 D．若，，则11．刍(chú)甍(méng)是中国古代算数中的一种几何体，其结构特征是：底面为长方形，上棱和底面平行，且长度不等于底面平行的棱长的五面体，是一个对称的楔形体．已知一个刍甍底边长为，底边宽为，上棱长为，高为，则它的表面积是（    ）A． B．C． D．12．若函数在区间上单调递增，则的取值范围是（    ）A． B． C． D． 二、填空题13．已知平面向量，，若，则实数________．14．已知，则_______．15．已知等差数列的前项和为，若，，，则符合题意的等差数列的一个通项公式为________．16．焦点为的抛物线上有一点，为坐标原点，则满足的点的坐标为_________． 三、解答题17．在中，内角A，B，C的对边分别为a，b，c，，且_________．在①，②这两个条件中任选一个，补充在上面横线中，并解答下列问题．注：如果选择多个条件分别解答，按第一个解答计分(1)求；(2)若，求．18．为提升学生实践能力和创新能力，某校在高一，高二年级开设“航空模型制作"选修课程．为考察课程开设情况，学校从两个年级选修该课程的学生中各随机抽取20名同学分别制作一件航空模型．并根据每位同学作品得分绘制了如图所示的茎叶图．若作品得分不低于80，评定为“优良”，否则评定为“非优良”．高一同学作品 高二同学作品     8832657        965432210713879         9622182345677899       539078       (1)请完成下面的2×2列联表； 优良非优良合计高一   高二   合计   (2)判断是否有的把握认为作品是否“优良”与制作者所处年级有关?附：，．0.1500.1000.0100.0012.0722.7066.63510.828 19．如图，在三棱柱中，平面ABC，D，E分别为AC，的中点，，．(1)求证：平面；(2)求点D到平面ABE的距离．20．已知函数．(1)求函数的极值；(2)若在上恒成立，求实数的取值范围．21．已知双曲线：的左，右焦点分别为，，离心率为，过焦点且垂直于轴的直线截双曲线所得弦长为．直线：与双曲线C的左支交于，两点，点A关于原点О对称的点为D．(1)求双曲线的方程；(2)证明：直线与圆O：相切．22．在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，直线的极坐标方程为.(1)写出直线的直角坐标方程；(2)若直线与曲线有公共点，求实数的取值范围.23．已知函数．(1)求的值域；(2)若的最大值为，正实数a，b，c满足，证明：．
参考答案：1．C2．D3．D4．A5．D6．A7．A8．B9．A10．C11．B12．B13．14．15．（答案不唯一）16．17．(1)(2) 18．(1)答案见解析；(2)有的把握认为作品是否“优良”与制作者所处年级有关． 19．(1)证明见解析；(2) 20．(1)极小值，无极大值．(2) 21．(1)(2)证明见解析 22．(1)(2) 23．(1)(2)证明见解析