
江西省新八校2023届高三第二次联考数学(文)试题(无解析)
展开江西省新八校2023届高三第二次联考数学(文)试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.记集合,,则( )
A. B. C. D.
2.已知复数,则的共轭复数为( )
A. B. C. D.
3.已知向量,,,则的值为( )
A.3 B.4 C. D.
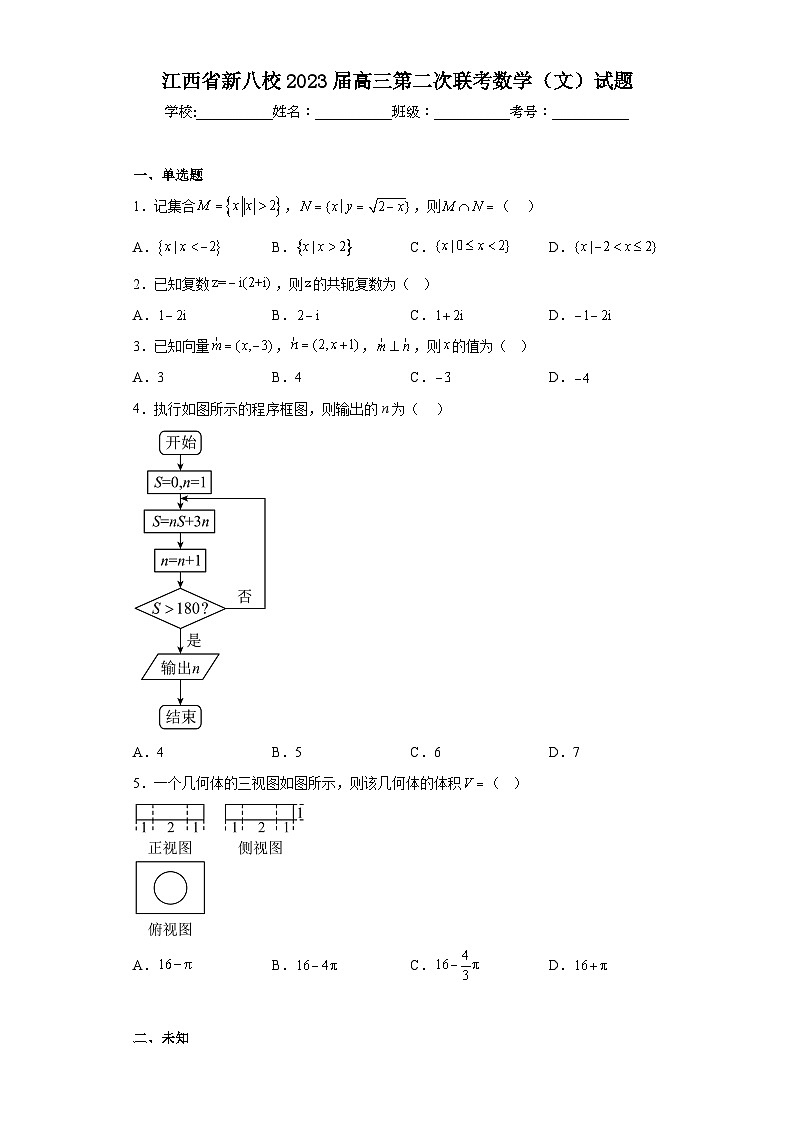
4.执行如图所示的程序框图,则输出的n为( )
A.4 B.5 C.6 D.7
5.一个几何体的三视图如图所示,则该几何体的体积( )
A. B. C. D.
二、未知
6.甲乙两位游客慕名来到赣州旅游,准备分别从大余丫山、崇义齐云山、全南天龙山、龙南九连山和安远三百山5个景点中随机选择其中一个,记事件A:甲和乙选择的景点不同,事件B:甲和乙恰好选择崇义齐云山,则条件概率( )
A. B. C. D.
7.已知递增的等差数列的首项为1,前项和为,且,,成等比数列.令,则数列的前50项和( )
A. B. C. D.
8.已知是函数的最大值,若存在实数、使得对任意实数总有成立,则的最小值为( )
A. B. C. D.
9.函数图像上存在不同的三点到原点的距离构成等差数列,则以下不可能成为公差的数是( )
A. B. C.1 D.
10.已知,,,则( )
A. B.
C. D.
三、单选题
11.古希腊数学家欧几里得在《几何原本》中描述了圆锥曲线的共性,并给出了圆锥曲线的统一定义,只可惜对这一定义欧几里得没有给出证明.经过了500年,到了3世纪,希腊数学家帕普斯在他的著作《数学汇篇》中完善了欧几里得关于圆锥曲线的统一定义,并对这一定义进行了证明.他指出,到定点的距离与到定直线的距离的比是常数的点的轨迹叫做圆锥曲线:当时,轨迹为椭圆;当时,轨迹为抛物线;当时,轨迹为双曲线.现有方程表示的曲线是双曲线,则的取值范围为( )
A. B. C. D.
12.设点在曲线上,点在曲线上,则的最小值为( )
A. B.
C. D.
四、填空题
13.已知x,y满足约束条件,则的最大值为__________.
14.已知函数,则不等式的解集是______.
五、未知
15.在棱长为2的正方体中,点为中点,点在正方形内运动(含边界),在点运动过程中,点到平面的最小距离是______.
16.已知是拋物线上两点,且,为焦点,则最大值为______.
17.为了有针对性地提高学生体育锻炼的积极性,某校需要了解学生是否经常锻炼与性别因素有关,为此随机对该校100名学生进行问卷调查,得到如下列联表.
| 经常锻炼 | 不经常锻炼 | 总计 |
男 | 35 |
|
|
女 |
| 25 |
|
总计 |
|
| 100 |
已知从这100名学生中任选1人,女生被选中的概率为.
(1)完成上面的列联表,并根据列联表中的数据,判断能否有的把握认为该校学生是否经常锻炼与性别因素有关.
(2)若按分层抽样法从女生中抽取8人,再从8人中随机抽取2人进行访谈,求抽取的2人都不经常锻炼的概率.
附:,其中,.
0.1 | 0.05 | 0.01 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
六、解答题
18.在中,内角所对的边分别为,且.
(1)求角的大小;
(2)若,,求的面积.
19.如图,在直三棱柱中,平面,其垂足落在直线上.
(1)求证:;
(2)若是线段AB上一点,,,三棱锥的体积为,求的值.
七、未知
20.已知圆A:,直线过点且与轴不重合,交圆于C,D两点,过作AC的平行线交AD于点E.
(1)求点E的轨迹的方程;
(2)设轨迹的上、下顶点分别为G、H,过点的直线交轨迹于M、N两点(不与G、H重合),直线GM与直线交于点,求证:P、H、N三点共线.
21.已知函数.
(1)若,求在点处的切线方程;
(2)若是的两个极值点,证明:.
22.在直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线的普通方程和直线的直角坐标方程;
(2)已知点的极坐标为,设曲线和直线交于M,N两点,求的值.
23.已知a,b,c为正实数,且满足.证明:
(1);
(2).
江西省新八校2023届高三数学(理)第二次联考试题(Word版附解析): 这是一份江西省新八校2023届高三数学(理)第二次联考试题(Word版附解析),共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江西省新八校2023届高三数学(文)第二次联考试题(Word版附解析): 这是一份江西省新八校2023届高三数学(文)第二次联考试题(Word版附解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江西省新八校2023届高三第二次联考数学(文)试题及答案: 这是一份江西省新八校2023届高三第二次联考数学(文)试题及答案,共20页。