北京市平谷区2023届初三中考数学一模试卷+答案

这是一份北京市平谷区2023届初三中考数学一模试卷+答案，共13页。试卷主要包含了选择题，填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
第1-8题均有四个选项，符合题意的选项只有一个.
1.下面几何体中，是圆柱体的为
A BCD
为了确保我国粮食种植的稳定性，国家提出了“严防死守18亿亩耕地的红线目标”，经过了多年的努力和坚守，我国耕地面积止住了下跌趋势，而且还实现了增长。到2020年，全国耕地保有量回升至18.65亿亩以上，1865000000用科学计数法表示为
A.B. C. D.
3.把一根细线固定在半圆形量角器的圆心处，细线的另一端系一个小重物，制成一个简单的测角仪，如图所示，细线与BC边重合，则∠A的度数为
A.30° B. 40°
C. 50°D. 75°
4.实数在数轴上的对应点的位置如图所示.若实数满足，则的值可以是
A.1 B. C. D.
5.不透明的袋子中有三个小球，上面分别写着数字“”“”“”，除数字外三个小球无其他差别.从中随机摸出一个小球，记录其数字，不放回，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为的概率是
A. B. C. D.
6.若关于的一元二次方程有两个不相等的实数根，则实数的取值范围为
A. B. C. D.
7.瓷器上的纹饰是中国古代传统文化的重要载体之一，如图所示的图片即为瓷器上的纹饰，该图形即为中心对称图形也为轴对称图形，该图形的对称轴的条数为
A.B.C.D.
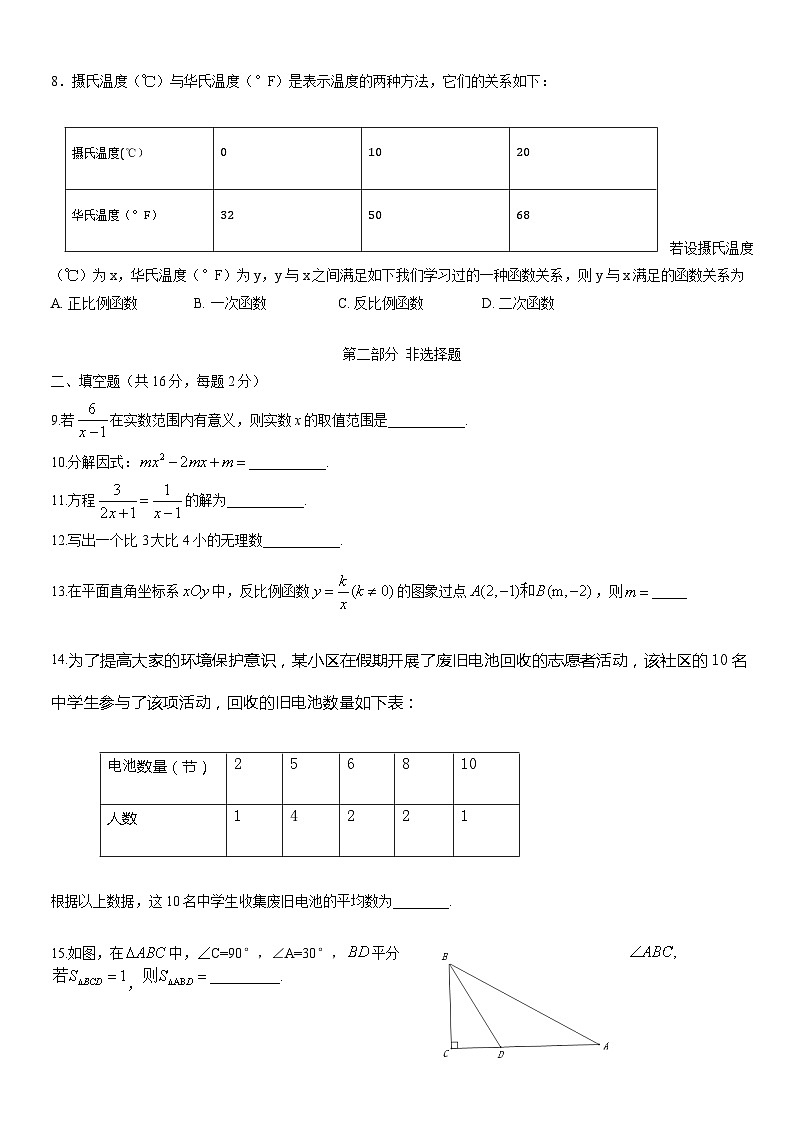
摄氏温度（℃）与华氏温度（°F）是表示温度的两种方法，它们的关系如下：
若设摄氏温度（℃）为x，华氏温度（°F）为y，y与x之间满足如下我们学习过的一种函数关系，则y与x满足的函数关系为
A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数
第二部分 非选择题
二、填空题（共16分，每题2分）
9.若在实数范围内有意义，则实数x的取值范围是___________.
10.分解因式：___________.
11.方程的解为___________.
12.写出一个比3大比4小的无理数___________.
13.在平面直角坐标系中，反比例函数的图象过点，则_____
14.为了提高大家的环境保护意识，某小区在假期开展了废旧电池回收的志愿者活动，该社区的10名中学生参与了该项活动，回收的旧电池数量如下表：
根据以上数据，这10名中学生收集废旧电池的平均数为________.
15.如图，在中，∠C=90°，∠A=30°，平分，__________.
16.某货运公司临时接到一个任务，从工厂同时运送A、B两种货物各20箱到展馆，货运公司调派甲货车运送A种货物，乙货车运送B种货物，A种货物每箱80千克，B种货物每箱70千克，因为两种货物包装箱完全一样，装运工人一时疏忽两车虽然所装货物数量正确，但部分货物却装混了.运送途中安检时，两车过地秤，发现甲车比乙车的货物重160千克，则甲、乙两车各有_____箱货物装错,到达展馆，为了尽快把货物区分开，乙车司机借来了一台最多可以称300千克的秤，精选最优称重方案，根据被错装货物出现的所有可能情况，最多需要称_______次就能把乙车上装错的货物区分出来.
三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程.
17.计算：
18.解不等式组：
19.已知求代数式的值.
20.已知：如图，为锐角三角形.
求作：以BC为一边作Rt△MBC，使∠MBC=90°，∠M=∠A.
作法：①作AC边的垂直平分线DE；
②作BC边的垂直平分线FG，与直线DE交于点O；
= 3 \* GB3 \* MERGEFORMAT ③以O为圆心，OA为半径作；
= 4 \* GB3 \* MERGEFORMAT ④连接CO并延长，交于点M，连接BM；
△MBC即为所求作的三角形
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明.
证明：∵DE是AC的垂直平分线，FG是BC的垂直平分线,DE与FG交于点O
∴OA=OB=OC
∴点A、B、C都在上
∵CM为的直径
∴°.
∵
∴（）（填推理依据）.
∴△MBC即为所求作的三角形.
21.如图，在中，点E是BC中点，点F是中点，连接AE、CF、EF，平分∠AEC.
（1）求证：四边形是菱形；
（2）连接AC与EF交于点O，连接OD，若AF=5，，求OD的长.
22.在平面直角坐标系中，函数的图象经过点.
（1）求该函数的解析式；
（2）当时，对于的每一个值，函数的值大于函数的值，求的取值范围.
23.明明学完了统计部分的相关知识后,对数据的统计产生了浓厚的兴趣,他从网上查阅了2023年3月1号至10号A、B两个城市的日最高气温数据,并对数据进行整理、描述和分析，下面给出了部分信息.
a.A、B两个城市3月1号至10号的日最高气温数据的折线图：
b.A、B两个城市3月1号至10号的日最高气温数据的平均数、中位数、众数、极差：
根据以上信息，回答下列问题：
（1）求表中m、n、z的值；
（2）记A城市3月1号至10号的日最高气温的方差为，B城市3月1号至10号的日最高气温的方差为，
则_________（填“>”“；4
(3)A城市3月1日至10日日平均气温的平均值更高，极差较大，温度波动较大，不稳定，
B城市3月1日至10日日平均气温的平均值较小，极差小，温度变化较稳定。
6
24．（1）解：连结OD．
∵DE为
∴∠EDO=90°1
∵ ∴∠1=∠2．
∵OA=OD
∴∠2=∠32
∴∠1=∠3∴OD∥AE
∴∠E=∠EDO=90°3
（2）∵四边形ABDC内接于⊙
∴∠B=∠ECD4
∵AB是直径∴∠ADB=90°，∵AB=9
∴BD=65
∵ ∴CD=BD=6，
∴CE=46
25.（1）由表可知，抛物线的顶点坐标为（3,4.4）
∴抛物线的解析式为∵抛物线过点（0.3.5）.解得a=-0.1
2
当y=1.9时，x=8
3
（2） = 2 \* GB3 \* MERGEFORMAT ②； = 1 \* GB3 \* MERGEFORMAT ①.5
26.（1）解：对称轴x=m 1
（2）3
（3）4
5
6
27.(1)补全图形
(2) 证明：
∵∠BDC=90°
∴∠DCF+∠DFC=90°
∵EM⊥EF
∴∠EMF+∠EFM=90°
∵∠EFM=∠DFC
∴∠EMF=∠
（3）
延长ME到G使EG=EM，连接AG、CG
∵∠GEA=∠MEB，EG=EM，AE=BE
∴△AGE≌△BME（SAS）
∴BM=AG,BM∥AG
∵BD⊥AC
∴∠GAC=∠BDA=90°
∵CE⊥EM，EM=EG
∴CE垂直平分MG ∴CG=CM
在Rt△AGC中，
28．解：（1）Q1，Q3；2
（2）4
（3）
如图，点A的所有对炫点在以B为圆心半径为1的圆上，点P的所有对炫点在互相平行的l1、l2两条直线围成的区域内，所以满足条件的时刻即为圆B与l1、l2两条直线围成的区域内有交点即可
5
∴，7摄氏温度(℃）
0
10
20
华氏温度（°F）
32
50
68
电池数量（节）
2
5
6
8
10
人数
1
4
2
2
1
城市
平均数
中位数
众数
极差
A
17.5
17.5
19
z
B
12.4
m
n
8
水平距离x/m
0
2
3
4
5
竖直高度y/m
3.5
4.3
4.4
4.3
4.0
题号
1
2
3
4
5
6
7
8
答案
A
C
B
D
B
D
C
B
题号
9
10
11
12
13
14
15
16
答案
x=4
答案不唯一例：
1
6
2
2;8