浙教版八年级下册6.3 反比例函数的应用背景图ppt课件

这是一份浙教版八年级下册6.3 反比例函数的应用背景图ppt课件，共18页。PPT课件主要包含了增减性，图象是双曲线，变化趋势，对称性，情景导入，∴k6000等内容，欢迎下载使用。

反比例函数的图象性质特征.
当k>0时,双曲线分别位于第一,三象限内当k<0时, 双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与坐标轴相交
双曲线既是轴对称图形又是中心对称图形.
设1根火柴的长度为1，能否用若干根火柴首尾相接摆出一个面积为12的矩形？面积为12的正方形呢？
在现实世界中，成反比例的量广泛存在着.用反比例函数的表达式和图象表示问题情境中成反比例的量之间的关系，能帮助我们分析和判断问题情境中的有关过程和结果，确定变量在一定条件下的特殊值或特定的范围，了解变量的变化规律.
例1 设△ABC中BC边的长为x（cm），BC上的高AD为y（cm）。 △ABC的面积为常数.已知y关于x的函数图象过点（3，4）.
(1) 求y关于x的函数解析式和△ABC 的面积
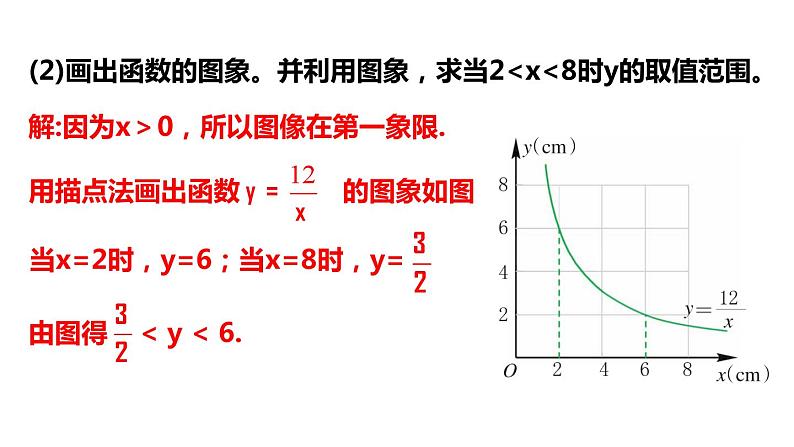
(2)画出函数的图象。并利用图象，求当2解:因为x＞0，所以图像在第一象限.
用反比例函数解决实际问题的步骤
(1)把图象上的某一点作为切入点,确定反比例函数的表达式;(2)构造方程或不等式解决问题.
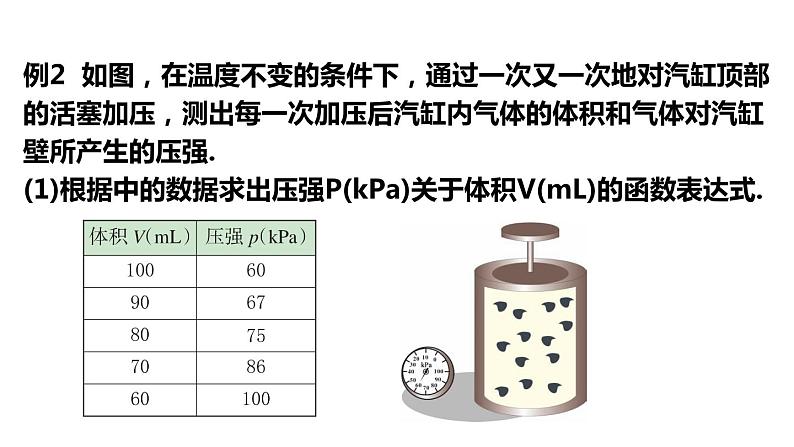
例2 如图，在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后汽缸内气体的体积和气体对汽缸壁所产生的压强.(1)根据中的数据求出压强P(kPa)关于体积V(mL)的函数表达式.
解 （1）根据表中的数据，可画出p关于V的函数图像.
（2）当压力表读出的压强为72 kPa时汽缸内气体的体积压缩到多少毫升？
答：当压力表中读出压强为72kPa时，汽缸内气体的体积约为83mL.
建立反比例函数模型的过程
(1)由实验获得数据;(2)用描点法画出图象;(3)根据图象和数据判断或估计函数的类别;(4)用待定系数法求出函数关系式;(5)用实验数据验证函数关系式;(6)应用函数关系式解决问题.
1.某学校要种植一块面积为200 m2的矩形草坪,要求相邻两边长均不小于10 m,则草坪的一边长y(单位:m)随其相邻的另一边长x(单位:m)的变化而变化的图象可能是(　　)
5.某蓄水池的排水管每小时排水8 m3,6 h可将满池水全部排空.如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间为t(h).写出时间t与Q之间的函数表达式:　　　　 . 
7.[2018·衢州一模] 当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:
则p与V之间的函数表达式可能是(　　)
6.某空调厂的装备车间计划组装9000台空调.(1)从组装空调开始,每天组装的台数m与生产的时间t(单位:天)之间有怎样的函数关系?并求出其函数表达式;(2)原计划用两个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少台空调?