初中北师大版第五章 生活中的轴对称2 探索轴对称的性质随堂练习题
展开5.2探索轴对称的性质
一、单选题
1.如图,在编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形是( )
A. ①和② B. ②和③ C. ①和③ D. ②和④
2.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为( )
A. 35° B. 53° C. 63° D. 43°
3.如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=82°,则原三角形的∠B为( )
A. 75° B. 76° C. 77° D. 78°
4.在平面直角坐标系中,以点A(2,4)为圆心,1为半径作⊙A,以点B(3,5)为圆心,3为半径作⊙B,M、N分别是⊙A,⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
A. -4 B. -1 C. 6-2 D. -3
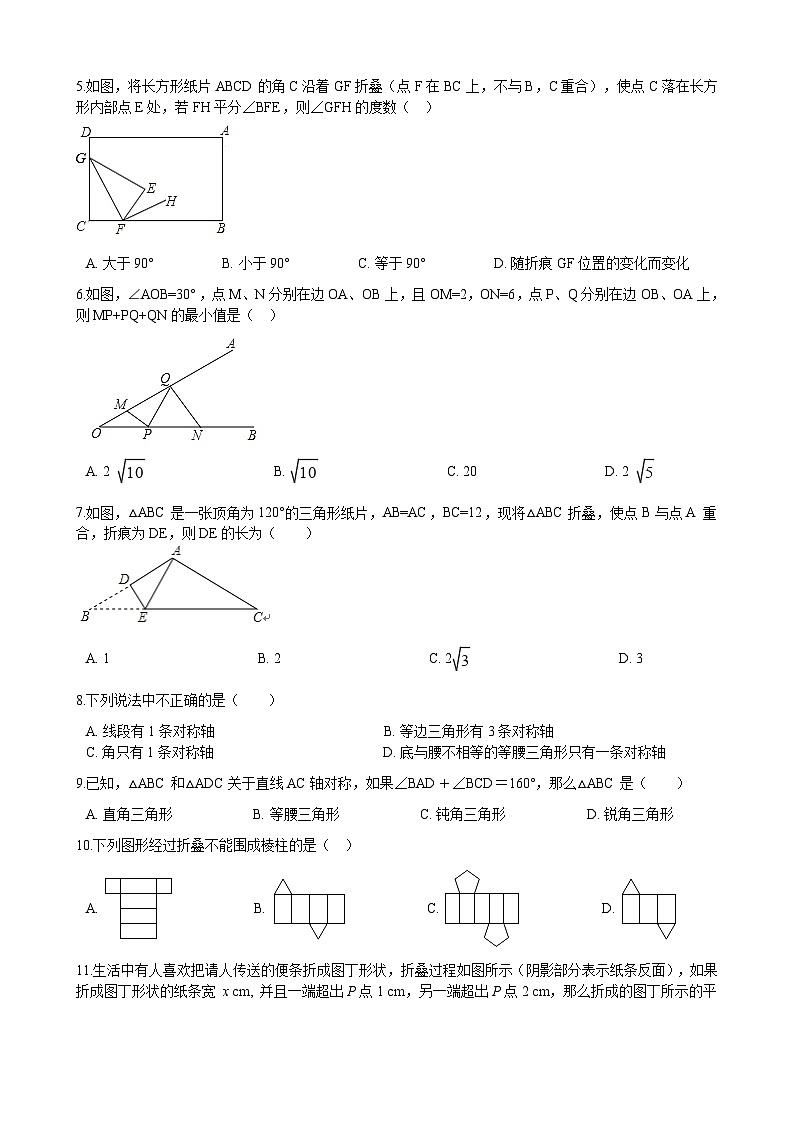
5.如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
A. 大于90° B. 小于90° C. 等于90° D. 随折痕GF位置的变化而变化
6.如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
A. 2 B. C. 20 D. 2
7.如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
A. 1 B. 2 C. 2 D. 3
8.下列说法中不正确的是( )
A. 线段有1条对称轴 B. 等边三角形有3条对称轴
C. 角只有1条对称轴 D. 底与腰不相等的等腰三角形只有一条对称轴
9.已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )
A. 直角三角形 B. 等腰三角形 C. 钝角三角形 D. 锐角三角形
10.下列图形经过折叠不能围成棱柱的是( )
A. B. C. D.
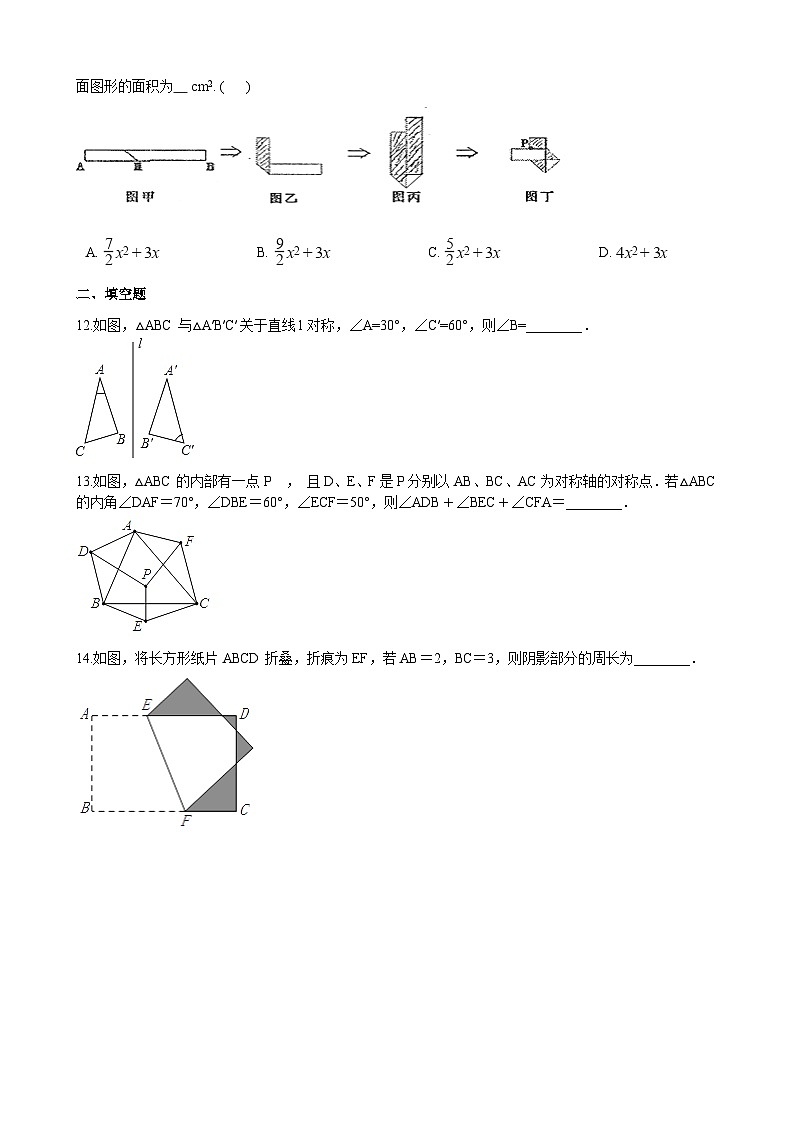
11.生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程如图所示(阴影部分表示纸条反面),如果折成图丁形状的纸条宽 x cm, 并且一端超出P点1 cm,另一端超出P点2 cm,那么折成的图丁所示的平面图形的面积为 cm2. ( )
A. B. C. D.
二、填空题
12.如图,△ABC与△A′B′C′关于直线l对称,∠A=30°,∠C′=60°,则∠B=________.
13.如图,△ABC的内部有一点P , 且D、E、F是P分别以AB、BC、AC为对称轴的对称点.若△ABC的内角∠DAF=70°,∠DBE=60°,∠ECF=50°,则∠ADB+∠BEC+∠CFA=________.
14.如图,将长方形纸片ABCD折叠,折痕为EF,若AB=2,BC=3,则阴影部分的周长为________.
15.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=3cm,PN=4cm,MN=4.5cm,则线段QR的长为________.
16.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是________
17.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=________°.
三、解答题
18.如图,把一张长方形纸片ABCD沿AF折叠,使B点落在B′处,若∠ADB=20°,那么∠BAF应为多少度时才能使AB′∥BD?
19.如图,△ABC和△A′B′C′关于直线l对称,求证:△ABC≌△A′B′C′.若△ABC≌△A′B′C′,那么△ABC和△A′B′C′一定关于某条直线l对称吗?若一定请给出证明,若不一定请画出反例图。
20.如图,l是线段AB的对称轴,l′是线段BC的对称轴,l和l′相交于点O.OA与OC相等吗?为什么?
四、综合题(
21.如图,△ABC和△A′B′C′关于直线m对称。
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其它对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流。
22.如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH.
(1)求证:∠APB=∠BPH.
(2)求证:AP+HC=PH.
(3)当AP=1时,求PH的长.
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】由图象可知,关于x轴折叠后,②和③能够完全重合,
所以,关于x轴对称的两个三角形是②和③.
故选B.
【分析】根据轴对称的性质,找出关于x轴折叠后能够完全重合的两个三角形即可.
2.【答案】B
【解析】【解答】解:∵△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,
∴∠C=25°,
∴∠B=180°﹣∠A﹣∠C=53°.
故选:B.
【分析】利用轴对称图形的性质得出∠C=25°,进而利用三角形内角和定理得出即可.
3.【答案】D
【解析】【解答】解:在△ABC中,∠A=30°,则∠B+∠C=150°…①; 根据折叠的性质知:∠B=3∠CBD,∠BCD=∠C;
在△CBD中,则有:∠CBD+∠BCD=180°﹣82°,即: ∠B+∠C=98°…②;
①﹣②,得: ∠B=52°,
解得∠B=78°.
故选D.
【分析】在图①的△ABC中,根据三角形内角和定理,可求得∠B+∠C=150°;结合折叠的性质和图②③可知:∠B=3∠CBD,即可在△CBD中,得到另一个关于∠B、∠C度数的等量关系式,联立两式即可求得∠B的度数.
4.【答案】A
【解析】【解答】解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
则此时PM+PN最小,
∵点A坐标(2,4),
∴点A′坐标(2,﹣4),
∵点B(3,5),
∴A′B=
∴MN=A′B﹣BN﹣A′M=5﹣3﹣1=﹣4,
∴PM+PN的最小值为﹣4.
故选A.
【分析】作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到PM+PN的最小值.
5.【答案】C
【解析】【解答】
解::∵△GFE是由△GFC沿GF折叠,
∴∠1=∠3= ∠CFE,
∵FH平分∠BFE,
∴∠2=∠4= ∠EFB,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=90°,
即∠GFH=90°.
故答案为:90°.
【分析】根据折叠的性质可知∠1=∠3= ∠CFE,根据已知条件FH平分∠BFE,可得∠2=∠4= ∠EFB,最后由∠1、∠2、∠3、∠4的和为180°可求∠GFH的度数。
6.【答案】A
【解析】【解答】解:作M关于OB的对称点M′,作N关于OA的对称点N′,如图所示: 连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′= =2 .
故选:A.
【分析】作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值;证出△ONN′为等边三角形,△OMM′为等边三角形,得出∠N′OM′=90°,由勾股定理求出M′N′即可.
7.【答案】B
【解析】【解答】解:∵∠BAC=120°,
∴∠B=∠C=30°,
根据折叠的性质,AE=BE,∠DAE=∠B=30°,
∴∠EAC=90°,
∴AE=EC,
∵BC=12,
∴AE=4,
∵∠ADE=90°,∠DAE=30°,
∴DE=2.
故选:B.
【分析】根据折叠的性质,AE=BE,∠DAE=∠B=30°,又∠BAC=120°,可知∠EAC=90°,根据30°所对的直角边等于斜边的一半,可知AE=4,DE=2.
8.【答案】A
【解析】【解答】线段有本身所在的直线和垂直平分线2条对称轴,A错误;
等边三角形有三条高所在的直线3条对称轴,B正确;
角只有角平分线所在的直线1条对称轴,C正确;
底与腰不相等的等腰三角形只有一条对称轴,D正确,
故选:A.
【分析】根据轴对称图形的概念和具体图形确定各个选项中图形的对称轴,判断得到答案.
9.【答案】C
【解析】【解答】如图,∵△ABC和△ADC关于直线AC轴对称,
∴∠BAC=∠DAC , ∠ACB=∠ACD ,
∴∠BAC+∠ACB= (∠BAD+∠BCD)= ×160°=80°,
在△ABC中,∠B=180°-(∠BAC+∠ACB)=180°-80°=100°,
∴△ABC是钝角三角形.
故选C.
【分析】作出图形,根据轴对称的性质可得∠BAC=∠DAC , ∠ACB=∠ACD , 然后求出∠BAC+∠ACB , 再根据三角形的内角和定理求出∠B , 然后判断三角形的形状即可.
10.【答案】B
【解析】【解答】解:A可以围成四棱柱,C可以围成五棱柱,D可以围成三棱柱,B选项侧面上多出一个长方形,故不能围成一个三棱柱.
故选:B.
【分析】由平面图形的折叠及棱柱的展开图解题.
11.【答案】C
【解析】【解答】如图,
根据折叠的性质可知:
AO=AC+CO=2+x,BP=1,
等腰直角三角形的直角边为x,
则S=AO⋅x+BP⋅x+3× x2=2x+x2+x+ x2= x2+3x,
故答案为:C.
【分析】根据折叠的性质可知,该图形的是由两个矩形和三个等腰直角三角形组合而成的,故只需求出矩形和等腰直角三角形的面积即可求解.
二、填空题
12.【答案】90°
【解析】【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴∠C=∠C′=60°,
在△ABC中,∠B=180°﹣∠A﹣∠C=180°﹣30°﹣60°=90°.
故答案为:90°.
【分析】根据轴对称的性质可得∠C=∠C′,再根据三角形的内角和等于180°列式计算即可得解.
13.【答案】360°
【解析】【解答】连接AP , BP , CP ,
∵D , E , F是P分别以AB , BC , AC为对称轴的对称点
∴∠ADB=∠APB , ∠BEC=∠BPC , ∠CFA=∠APC ,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
故答案为:360°.
【分析】连接AP , BP , CP后,根据轴对称的性质,可得到角相等,结合周角的定义可知答案.
14.【答案】10
【解析】【解答】
∵AE=ME,AB=MN,BF=NF,
∴ME+DE+MN+CD+CF+NF
=AE+DE+AB+CD+CF+BF
=AD+AB+CD+BC
=2+3+2+3
=10.
【分析】根据图形求出ME+DE+MN+CD+CF+NF=AE+DE+AB+CD+CF+BF=AD+AB+CD+BC的值.
15.【答案】5.5cm
【解析】【解答】解:∵点P关于OA的对称点Q恰好落在线段MN上, ∴OA垂直平分PQ,
∴QM=PM=3cm,
∴QN=MN﹣QM=4.5cm﹣3cm=1.5cm,
∵点P关于OB的对称点R落在MN的延长线上,
∴OB垂直平分PR,
∴RN=PN=4cm,
∴QR=QN+RN=1.5cm+4cm=5.5cm.
故答案为5.5cm.
【分析】根据轴对称的性质得到OA垂直平分PQ,OB垂直平分PR,则利用线段垂直平分线的性质得QM=PM=3cm,RN=PN=4cm,然后计算QN,再计算QN+EN即可.
16.【答案】
【解析】【解答】解:如图1所示
作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=AE′=2;CQ=DC﹣CQ=3﹣2=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,
,BP=, CP=BC﹣BP=3﹣=,
S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣SBEP=9﹣AD•DQ﹣CQ•CP﹣BE•BP
=9﹣×3×2﹣×1×﹣×1×=,
故答案为:.
【分析】根据最短路径的求法,先确定点E关于BC的对称点E′,再确定点A关于DC的对称点A′,连接A′E′即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ的面积.
17.【答案】15
【解析】【解答】解:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,
∴∠NPM=2×75°=150°,
∴∠C′PB=30°,
由折叠的性质可知:∠C′PN=∠BPN,
∴∠NPB′=15°.
故答案为:15.
【分析】两次运用折叠的性质可求解。
三、解答题
18.【答案】解:∵长方形纸片ABCD沿AF折叠,使B点落在B′处, ∴∠B′AF=∠BAF,
∵AB′∥BD,
∴∠B′AD=∠ADB=20°,
∴∠B′AB=20°+90°=110°,
∴∠BAF=110°÷2=55°.
∴∠BAF应为55度时才能使AB′∥BD
【解析】【分析】根据折叠的性质得到∠B′AF=∠BAF,要AB′∥BD,则要有∠B′AD=∠ADB=20°,从而得到∠B′AB=20°+90°=110°,即可求出∠BAF.
19.【答案】解:∵△ABC和△A′B′C′关于直线l对称,∴△ABC和△A′B′C′能够完全重合,
∴△ABC≌△A′B′C′。
若△ABC≌△A′B′C′,△ABC和△A′B′C′不一定一定关于某条直线l对称,如图所示.
【解析】【分析】轴对称的定义;把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称;根据定义可得△ABC和△A′B′C′能够完全重合,则△ABC≌△A′B′C′。若△ABC≌△A′B′C′,△ABC和△A′B′C′不一定一定关于某条直线l对称,如平行四边形的对角线分得的两个三角形全等但不对称。
20.【答案】解:∵l是线段AB的对称轴,∴OA=OB,
∵l′是线段BC的对称轴,
∴OB=OC,
∴OA=OC。
【解析】【分析】轴对称图形的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。根据性质可得OA=OB,OB=OC,所以OA=OC。
四、综合题
21.【答案】(1)解:对称点有A和A′,B和B′,C和C′
(2)解:连接A、A′,直线m是线段AA′的垂直平分线
(3)解:延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上,即若两线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴上。
【解析】【分析】(1)轴对称的定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称。根据定义可知对称点有A和A′,B和B′,C和C′。
(2)轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;根据性质可知直线m是线段AA′的垂直平分线。
(3)轴对称的性质:两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上。根据性质可知延长线段AC与A′C′,它们的交点在直线m上,其它对应线段(或其延长线)的交点也在直线m上。
22.【答案】(1)证明:∵PE=BE,
∴∠EPB=∠EBP,
又∵∠EPH=∠EBC=90°,
∴∠EPH﹣∠EPB=∠EBC﹣∠EBP.
即∠BPH=∠PBC.
又∵四边形ABCD为正方形
∴AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)证明:过B作BQ⊥PH,垂足为Q,
由(1)知,∠APB=∠BPH,
在△ABP与△QBP中,
∴△ABP≌△QBP(AAS),
∴AP=QP,BA=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,
∴△BCH和△BQH是直角三角形,
在Rt△BCH与Rt△BQH中,
∴Rt△BCH≌Rt△BQH(HL),
∴CH=QH,
∴AP+HC=PH.
(3)解:由(2)知,AP=PQ=1,
∴PD=3.
设QH=HC=x,则DH=4﹣x.
在Rt△PDH中,PD2+DH2=PH2 ,
即32+(4﹣x)2=(x+1)2 ,
解得x=2.4,
∴PH=3.4.
【解析】【分析】(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;
(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出AP+HC=PH;
(3)设QH=HC=x,则DH=4﹣x.在Rt△PDH中,根据勾股定理列出关于x的方程求解即可.
数学七年级下册第五章 生活中的轴对称2 探索轴对称的性质精品复习练习题: 这是一份数学七年级下册<a href="/sx/tb_c10002_t7/?tag_id=28" target="_blank">第五章 生活中的轴对称2 探索轴对称的性质精品复习练习题</a>,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级下册2 探索轴对称的性质课堂检测: 这是一份初中数学北师大版七年级下册2 探索轴对称的性质课堂检测,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级下册第五章 生活中的轴对称2 探索轴对称的性质同步测试题: 这是一份初中数学北师大版七年级下册第五章 生活中的轴对称2 探索轴对称的性质同步测试题,共6页。试卷主要包含了如图,直线l,m相交于点O等内容,欢迎下载使用。