数学（江苏扬州卷）2023年中考考前最后一卷（考试版）A4

2023年中考考前最后一卷

数  学

（考试时间：120分钟  试卷满分：150分）

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.写在本试卷上无效.

3．回答第Ⅱ卷时，将答案写在答题卡上.写在本试卷上无效.

4．考试结束后，将本试卷和答题卡一并交回.

第Ⅰ卷

一．选择题（共8小题，满分24分，每小题3分）

1．实数，，0，中最小的数是(   )

A．0 B． C． D．

2．下列运算中，正确的是（    ）

A． B． C． D．

3．如图，直线，，，则的度数是（    ）

A．85° B．80° C．90° D．100°

4．已知方程的两个根分别为、，则的值为（    ）

A．7 B．5 C．3 D．2

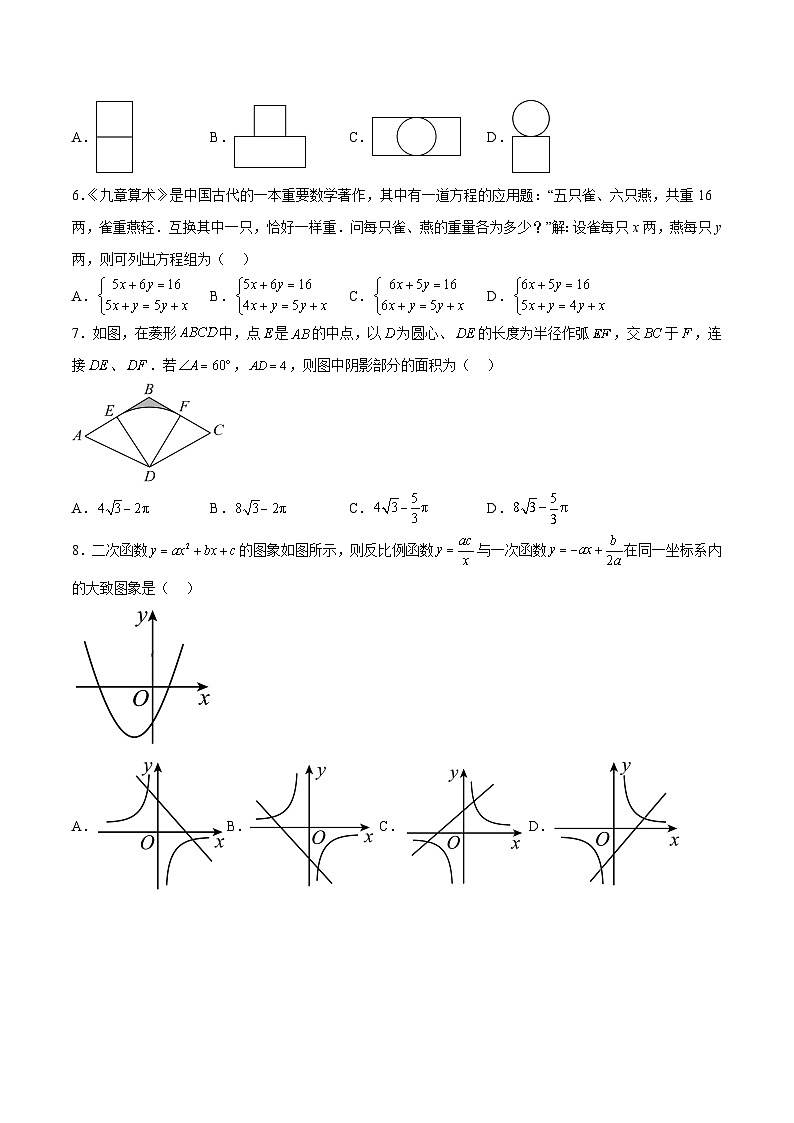
5．如图所示的几何体由一个圆柱体和一个长方体组成，它的俯视图是（    ）

A． B． C． D．

6．《九章算术》是中国古代的一本重要数学著作，其中有一道方程的应用题：“五只雀、六只燕，共重16两，雀重燕轻．互换其中一只，恰好一样重．问每只雀、燕的重量各为多少？”解：设雀每只x两，燕每只y两，则可列出方程组为（    ）

A． B． C． D．

7．如图，在菱形中，点是的中点，以为圆心、的长度为半径作弧，交于，连接、．若，，则图中阴影部分的面积为（    ）

A． B． C． D．

8．二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系内的大致图象是（    ）

A．B．C．D．

第Ⅱ卷

二．填空题（共10小题，满分30分，每小题3分）

9．若式子在实数范围内有意义，则的取值范围是___________．

10．分解因式：______．

11．粮食是人类赖以生存的重要物质基础.2022年我国粮食总产量再创新高，达68653万吨．该数据可用科学记数法表示为 _______________万吨．

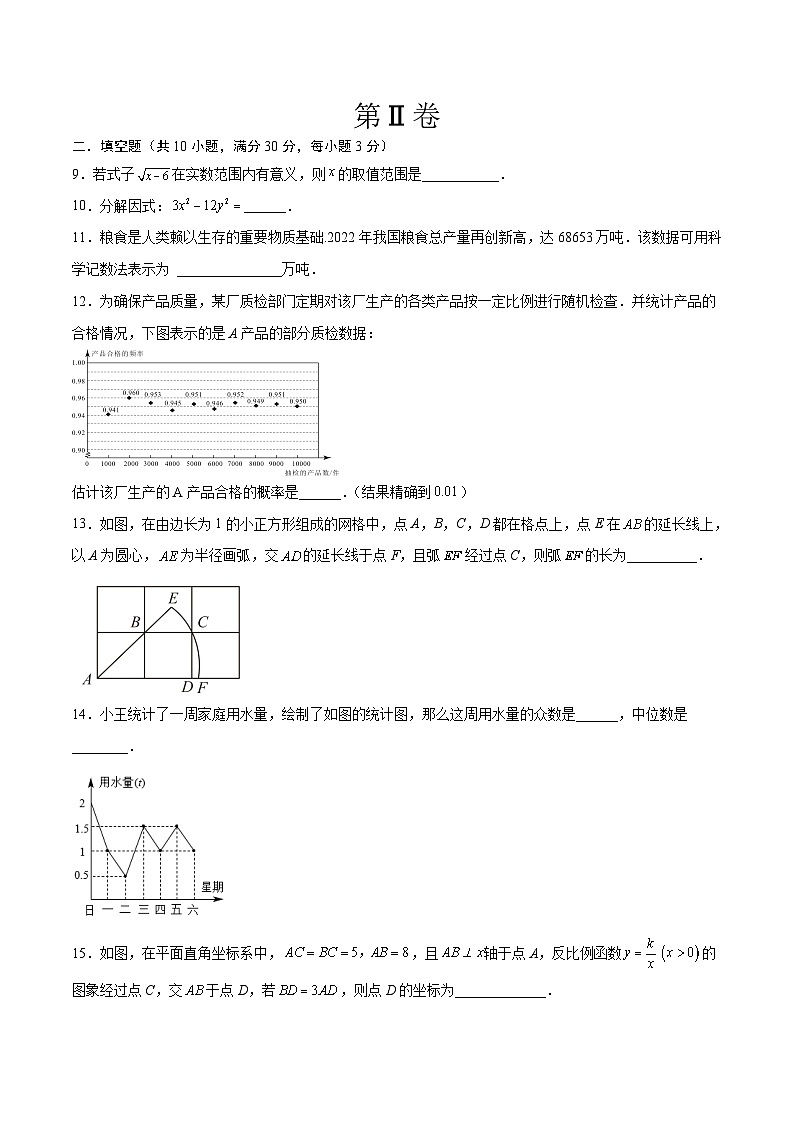
12．为确保产品质量，某厂质检部门定期对该厂生产的各类产品按一定比例进行随机检查．并统计产品的合格情况，下图表示的是A产品的部分质检数据：

估计该厂生产的A产品合格的概率是______．（结果精确到）

13．如图，在由边长为1的小正方形组成的网格中，点A，B，C，D都在格点上，点E在的延长线上，以A为圆心，为半径画弧，交的延长线于点F，且弧经过点C，则弧的长为__________．

14．小王统计了一周家庭用水量，绘制了如图的统计图，那么这周用水量的众数是______，中位数是________．

15．如图，在平面直角坐标系中，，且轴于点A，反比例函数的图象经过点C，交于点D，若，则点D的坐标为_____________．

16．中国人最先使用负数，魏晋时期的数学家刘徽在其著作《九章算术注》中，用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（红色为正，黑色为负）．如图1表示的算式是，根据这种表示法，可推算出图2所表示的算式是_______．

17．已知是关于的函数，若该函数的图象经过点，则称点为函数图象上的“平衡点”，例如：直线上存在“平衡点”，若函数的图象上存在唯一“平衡点”，则___________．

18．在边长为的正方形中，点是射线上的动点（不与重合），连接 ，将沿向右翻折得，连接和，若为等腰三角形，则的长为___________．

三．解答题（共10小题，共96分）

19．(8分)（1）计算：．

（2）如图，将两个全等的等腰直角三角形摆成如图所示的样子（图中所有的点、线都在同一平面内），求证：．

20．(8分)先化简，再求值：，其中x是不等式组的整数解

21．(8分)如图是由小正方形组成的网格，每个小正方形的顶点叫做格点的三个顶点都是格点仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线示．

(1)在图中，先在边上找一点，使，再画点关于点对称的点；

(2)在图中，是边上一点，先画的角平分线，再画点关于直线对称的点．

22．(8分)如图1是一张折叠型方桌子，图2是其侧面结构示意图，支架与交于点O，测得，．

(1)若，求的长；

(2)将桌子放平后，要使距离地面的高为，求两条桌腿需叉开角度．

23．(10分)随着时代发展，人们乘坐公交车支付车票的方式更加多样、便捷．某校数学实践小组设计了一份公交车票支付方式调查问卷，要求每位被调查人选且只选一种最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图．

根据所给的信息解答下列问题；

(1)这次活动共调查了______人；在扇形统计图中表示“微信”支付的扇形圆心角的度数为______；

(2)将条形统计图补充完整；

(3)小明和小亮都没有公交卡，在乘车中，想从“微信”“支付宝”“现金”“云闪付”四种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．

24．(10分)如图，为的直径，C，D为上两点，连接，，，，线段与相交于点E，过点D作，交的延长线于点F．

(1)求证：是的切线；

(2)若，，，求的半径．

25．(10分)如图，在平面直角坐标系中，一次函数的图像与反比例函数的图像交于点，C两点．

(1)求反比例函数的解析式及点C的坐标；

(2)点P是线段上一点，过点P向x轴做垂线段，垂足为Q，连接，的面积是否存在最大值，若存在，请求出最大面积及点P坐标，若不存在，请说明理由．

26．(10分)为打造校园劳动实践基地，某学校计划在3月份购进甲、乙两种植株进行培育．已知甲植株的单价是乙植株单价的，用900元购买的甲植株数量比用600元购买的乙植株数量多10株．

(1)求甲、乙植株的单价分别是多少元．

(2)该学校决定购买甲、乙两种植株共150株，其中乙植株的数量不超过甲植株数量的，如何购进两种植株才能使费用最低，最低费用是多少？

27．(12分)定义：若直线与开口向下的抛物线有两个交点，则这两个交点之间的距离叫做这条抛物线的“反碟长”．如图，已知抛物线：与直线相交于，．

(1)抛物线的“反碟长”________．

(2)抛物线随其顶点沿直线向上平移，得到抛物线．

①当抛物线的顶点平移到点，抛物线的解析式是________．抛物线的“反碟长”是________．

②若抛物线的“反碟长”是一个偶数，则其顶点的纵坐标可能是________．（填写所有正确的选项）

A．15    B．16    C．24    D．25

③当抛物线的顶点和抛物线与直线的两个交点，构成一个等边三角形时（点在点左右），求点的坐标．

28．(12分)如图，两个全等的四边形和，其中四边形的顶点O位于四边形的对角线交点O．

(1)如图1，若四边形和都是正方形，则下列说法正确有_______．（填序号）

①；②重叠部分的面积始终等于四边形的；③．

(2)应用提升:如图2，若四边形和都是矩形，，写出与之间的数量关系，并证明．

(3)类比拓展:如图3，若四边形和都是菱形，，判断（1）中的结论是否依然成立；如不成立，请写出你认为正确的结论（可用表示），并选取你所写结论中的一个说明理由．