

2022-2023学年江西省南昌二中七年级(下)期中数学试卷(含解析)
展开
这是一份2022-2023学年江西省南昌二中七年级(下)期中数学试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江西省南昌二中七年级(下)期中数学试卷
一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)
1.下列实数中,最小的数是( )
A.0 B.﹣1 C.﹣3 D.
2.如图,笑脸盖住的点的坐标可能为( )
A.(﹣2,4) B.(1,2) C.(﹣2,﹣3) D.(2,﹣3)
3.若点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3.那么点P到直线l的距离是( )
A.小于3 B.3 C.不大于3 D.不小于3
4.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱:每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,羊价y钱,下面所列方程组正确的是( )
A. B.
C. D.
5.有一个数值转换器,原理如图,当输入的x为81时,输出的y是( )
A.9 B.3 C.±3 D.
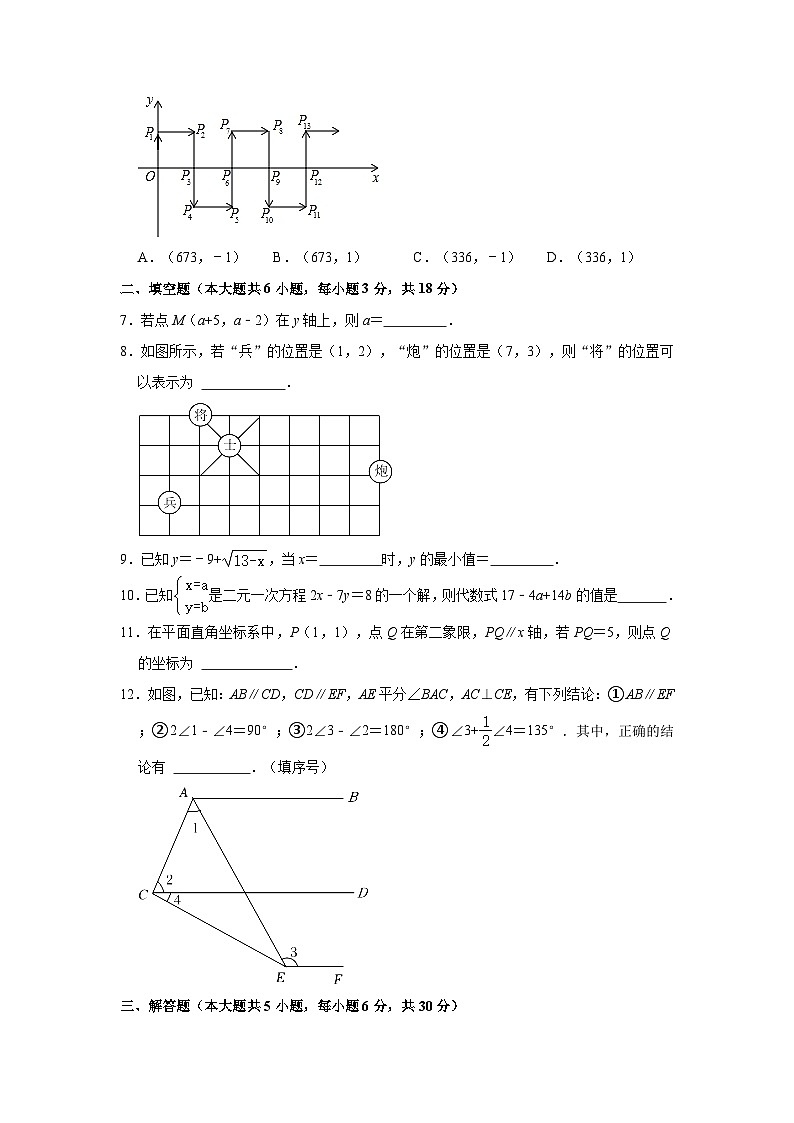
6.如图:在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…则点P2020的坐标是( )
A.(673,﹣1) B.(673,1) C.(336,﹣1) D.(336,1)
二、填空题(本大题共6小题,每小题3分,共18分)
7.若点M(a+5,a﹣2)在y轴上,则a= .
8.如图所示,若“兵”的位置是(1,2),“炮”的位置是(7,3),则“将”的位置可以表示为 .
9.已知y=﹣9+,当x= 时,y的最小值= .
10.已知是二元一次方程2x﹣7y=8的一个解,则代数式17﹣4a+14b的值是 .
11.在平面直角坐标系中,P(1,1),点Q在第二象限,PQ∥x轴,若PQ=5,则点Q的坐标为 .
12.如图,已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 .(填序号)
三、解答题(本大题共5小题,每小题6分,共30分)
13.计算:
(1);
(2).
14.(1)已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,求a+2b的平方根.
(2)若x、y都是实数,且y=++8,求x+y的值.
15.如图,有一只蚂蚁从点B沿数轴向左爬了2个单位长度到达点A,若点B表示数,设点A所表示的数为m.
(1)实数m的值是 ;
(2)求(m+2)2+|m+1|的值.
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d+8的平方根.
16.如图,已知∠1+∠2=180°,∠3=∠B,判断∠AED与∠C的大小关系.阅读下面的解答过程,填空并填写理由.
解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4 ( ).
∴AB∥EF( ).
∴∠3=( ).
又∵∠3=∠B(已知),
∴( )=∠B(等量代换).
∴DE∥BC( ).
∴∠AED=∠C( ).
17.小李同学想用一块面积为400cm2的正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,他不知道能否裁得出来,正在发愁,这时小于同学见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”
(1)长方形纸片的长和宽是分别多少cm?
(2)你是否同意小于同学的说法?说明理由.
三、(本大题共3小题,每小题8分,共24分)
18.我们知道,平方数的开平方运算可以直接求得,如等,有些数则不能直接求得,如,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请你观察下表:
a
…
0.04
4
400
40000
…
…
x
2
y
z
…
(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,= ;
(3)利用这一规律,解决下面的问题:
已知≈2.358,则①≈ ;②≈ .
19.如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(5,3),B(2,1),C(6,﹣2),三角形ABC中任意一点P(x0,y0),经平移后对应点为P'(x0﹣8,y0+2),将三角形ABC作同样的平移得到三角形A'B'C',点A,B,C的对应点分别为A',B',C'.
(1)点A'的坐标为 ,点B'的坐标为 ;
(2)求出三角形A'B'C'的面积;
(3)点D是x轴上一动点,当S△B'C'D=S△A'B'C'时,请直接写出点D的坐标 .
20.如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长是多少?
五、(本大题共2小题,每小题9分,共18分)
21.如图,在平面直角坐标系中,1cm对应坐标轴上的1个单位长度,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,以每秒1cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,两点都停止运动.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3s时,求三角形PQC的面积;
(3)设两点运动的时间为ts,当三角形OPQ的面积为16cm2时,求t的值(直接写出答案).
22.如图所示,A(1,0),点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,点C的坐标为(a,b),且.
(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是直线CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
六、(本大题共1小题,共12分)
23.为了保障学生安全,学校在操场两侧各安装了一枚探照灯,便于夜间对整个校园进行巡视.如图1,操场两侧MN∥PQ,且测得∠BAQ=45°.灯A射线自AP顺时针转至AQ便立即回转,灯B射线自BN顺时针转至BM便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,若灯B转动的速度是b°/秒,且a,b满足+|2b﹣4|=0.
(1)求a,b的值.
(2)若灯B射线先转动5秒,灯A射线才开始转动,在灯B射线与AB重合之前,灯A转动几秒,可以使两灯射线平行?(3)如图2,两灯同时转动,在灯B射线到达BM之前,若射出的光束交于点C,作∠NBC的角平分线交AC的延长线于点D.若t秒后,为定值,请你直接写出t的取值范围 .
参考答案
一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)
1.下列实数中,最小的数是( )
A.0 B.﹣1 C.﹣3 D.
【分析】根据正数大于0,0大于负数,两个负数,绝对值大的反而小比较.
解:∵正数和0都大于负数,
∴,
∴最小的数是﹣3,
故选:C.
【点评】本题考查了实数大小的比较,知道正数大于0,0大于负数,两个负数,绝对值大的反而小是解题的关键.
2.如图,笑脸盖住的点的坐标可能为( )
A.(﹣2,4) B.(1,2) C.(﹣2,﹣3) D.(2,﹣3)
【分析】根据图形得出笑脸的位置在第二象限,进而得出答案.
解:由图形可得:笑脸盖住的点在第二象限,
A、(﹣2,4)在第二象限,故本选项符合题意;
B、(1,2)在第一象限,故本选项不符合题意;
C、(﹣2,﹣3)在第三象限,故本选项不符合题意;
D、(2,﹣3)在第四象限,故本选项不符合题意.
故选:A.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.若点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3.那么点P到直线l的距离是( )
A.小于3 B.3 C.不大于3 D.不小于3
【分析】利用垂线段最短的性质,得出点P到直线l的距离取值范围.
解:∵点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3,
∴点P到直线l的距离是小于3.
故选:A.
【点评】此题主要考查了垂线段最短,利用PA=PD=3,得出点P到直线l的距离是解题关键.
4.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱:每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,羊价y钱,下面所列方程组正确的是( )
A. B.
C. D.
【分析】设合伙人数为x人,羊价为y钱,根据羊的价格不变列出方程组.
解:设合伙人数为x人,羊价为y钱,
根据题意,可列方程组为:.
故选:B.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系是解题的关键.
5.有一个数值转换器,原理如图,当输入的x为81时,输出的y是( )
A.9 B.3 C.±3 D.
【分析】将81 代入得9,9是有理数,再将9代入得3,3是有理数,再将3代入得,是无理数,故y=.
解:∵,9是有理数,
∴,3是有理数,
∴,,
∴,
故选:D.
【点评】本题考查了算术平方根,关键是根据题意求出值,再判断其是否为无理数.
6.如图:在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…则点P2020的坐标是( )
A.(673,﹣1) B.(673,1) C.(336,﹣1) D.(336,1)
【分析】由P3、P6、P9 可得规律:当下标为3的整数倍时,横坐标为,纵坐标为0,据此可解.
解:由P3、P6、P9 可得规律:当下标为3的整数倍时,横坐标为,纵坐标为0,
∵2019÷3=673,
∴P2019 (673,0)
则点P2019的坐标是 (673,0).
∴点P2020的坐标是(673,﹣1),
故选:A.
【点评】本题属于平面直角坐标系中找点的规律问题,找到某种循环规律之后,可以得解.本题难度中等偏上.
二、填空题(本大题共6小题,每小题3分,共18分)
7.若点M(a+5,a﹣2)在y轴上,则a= ﹣5 .
【分析】根据y轴上点的横坐标为0列出方程求解即可.
解:∵点M(a+5,a﹣2)在y轴上,
∴a+5=0,
解得a=﹣5.
故答案为:﹣5.
【点评】本题考查了点的坐标,熟记y轴上点的横坐标为0是解题的关键.
8.如图所示,若“兵”的位置是(1,2),“炮”的位置是(7,3),则“将”的位置可以表示为 (2,5) .
【分析】直接利用已知点坐标得出原式位置,进而得出答案.
解:由题意可建立平面直角坐标系如下图:
“将”所在的位置为(2,5),
故答案为:(2,5).
【点评】本题考查了坐标确定位置,正确画出平面直角坐标系,得出原点位置是解题的关键.
9.已知y=﹣9+,当x= 13 时,y的最小值= ﹣9 .
【分析】由算术平方根的非负性求解即可.
解:∵,
∴当x=13时,有最小值是0,
∴当x=13时,y有最小值,最小值为﹣9+0=﹣9,
故答案为:13;﹣9.
【点评】本题考查算术平方根的非负性,熟练掌握任何算术平方根是非负数是解题的关键.
10.已知是二元一次方程2x﹣7y=8的一个解,则代数式17﹣4a+14b的值是 1 .
【分析】将代入二元一次方程2x﹣7y=8得到2a﹣7b=8.再将代数式适当变形,利用整体代入可得代数式的值.
解:将代入二元一次方程2x﹣7y=8得:
2a﹣7b=8.
∴原式=17﹣2(2a﹣7b)=17﹣2×8=1.
故答案为:1.
【点评】本题主要考查了二元一次方程的解,利用整体代入求代数式的值.将方程的解代入原方程是解题的关键,
11.在平面直角坐标系中,P(1,1),点Q在第二象限,PQ∥x轴,若PQ=5,则点Q的坐标为 (﹣4,1) .
【分析】先根据PQ∥x轴可知P、Q两点纵坐标相同,再由PQ=5可得出Q点的横坐标.
解:∵P(1,1),PQ∥x轴,
∴Q两点纵坐标为1,
∵点Q在第二象限,PQ=5,
∴点Q的坐标为(﹣4,1).
故答案为:(﹣4,1).
【点评】本题考查的是坐标与图形性质,熟知各象限内点的坐标特点是解题的关键.
12.如图,已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 ①②③④ .(填序号)
【分析】根据平行线的性质逐一分析判断即可.
解:∵AB∥CD,CD∥EF,
∴AB∥EF,故①正确;
∵AE平分∠BAC,
∴∠BAC=2∠1,
∵AB∥CD,
∴∠BAC+∠2=180°,
∴2∠1+∠2=180°(1),
∵AC⊥CE,
∴∠2+∠4=90°(2),
∴(1)﹣(2)得,2∠1﹣∠4=90°,故②正确;
∵AB∥EF,
∴∠BAE+∠3=180°,
∵AE平分∠BAC,
∴∠1=∠BAE,
∴∠1+∠3=180°,
∴2∠1+2∠3=360°(3),
∵2∠1+∠2=180°(1),
(3)﹣(1)得,2∠3﹣∠2=180°,故③正确;
∵CD∥EF,
∴∠CEF+∠4=180°,
∴∠3+∠AEC+∠4=180°,
∵AC⊥CE,
∴∠1+∠AEC=90°,
∴∠AEC=90°﹣∠1,
∴∠3+∠4﹣∠1=90°,
∵2∠1﹣∠4=90°,
∴∠1=45°+∠4,
∴∠3+∠4=135°,故④正确.
故正确的结论有:①②③④.
故答案为:①②③④.
【点评】本题考查了平行线的判定和性质,熟练应用判定定理和性质定理是解题的关键,平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.
三、解答题(本大题共5小题,每小题6分,共30分)
13.计算:
(1);
(2).
【分析】(1)先化简各式,再进行加减运算;
(2)先化简各式,再进行加减运算.
解:(1)原式=
=2﹣3+2
=1;
(2)原式=
=.
【点评】本题考查实数的运算,熟练掌握实数的运算法则是解题的关键.
14.(1)已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,求a+2b的平方根.
(2)若x、y都是实数,且y=++8,求x+y的值.
【分析】(1)根据平方根的定义列式求出b,再根据算术平方根的定义列式求出a,然后求出a+2b的值,再根据平方根的定义解答即可;
(2)由二次根式有意义的条件得到关于x的不等式组,解不等式组即可求出x 的值,进一步即可求得结果.
解:(1)∵2b+1的平方根为±3,
∴2b+1=9,解得b=4,
∵3a+2b﹣1的算术平方根为4,
∴3a+2b﹣1=16,解得a=3,
∴a+2b=3+2×4=11,
∴a+2b的平方根是±.
(2)由题意得:,解得,所以x=3,
当x=3时,y=8,所以x+y=3+8=11.
【点评】本题考查了平方根和算术平方根的定义以及二次根式有意义的条件,属于基础题目,熟知概念是解题的关键.
15.如图,有一只蚂蚁从点B沿数轴向左爬了2个单位长度到达点A,若点B表示数,设点A所表示的数为m.
(1)实数m的值是 ;
(2)求(m+2)2+|m+1|的值.
(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+4|与互为相反数,求2c+3d+8的平方根.
【分析】(1)根据两点间的距离公式,直接右边的数减去距离即得左边的数;
(2)代入m求值即可;
(3)根据非负数的性质,求得c,d的值,代入即可求解.
解:(1)(1),
故答案为:;
(2)(m+2)2+|m+1|
=
=
=,
故答案为:.
(3)∵|2c+4|与互为相反数,
∴|2c+4|+=0,
∵|2c+4|≥0,≥0,
∴|2c+4|=0,=0,
∴c=﹣2,d=4,
∴2c+3d+8=2×(﹣2)+3×4+8=16,
∴.
【点评】本题考查的是两点间的距离公式、非负数的性质,关键是要会理解两点间的距离,最后求的平方根有两个.
16.如图,已知∠1+∠2=180°,∠3=∠B,判断∠AED与∠C的大小关系.阅读下面的解答过程,填空并填写理由.
解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4 ( 同角的补角相等 ).
∴AB∥EF( 内错角相等,两直线平行 ).
∴∠3=( ∠ADE ).
又∵∠3=∠B(已知),
∴( ∠ADE )=∠B(等量代换).
∴DE∥BC( 同位角相等,两直线平行 ).
∴∠AED=∠C( 两直线平行,同位角相等 ).
【分析】根据平行线的判定与性质即可完成填空.
解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4 (同角的补角相等).
∴AB∥EF(内错角相等,两直线平行).
∴∠3=∠ADE.
又∵∠3=∠B(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠C(两直线平行,同位角相等)
故答案为:同角的补角相等,内错角相等,两直线平行;∠ADE,∠ADE,同位角相等,两直线平行;两直线平行,同位角相等.
【点评】本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
17.小李同学想用一块面积为400cm2的正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,他不知道能否裁得出来,正在发愁,这时小于同学见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”
(1)长方形纸片的长和宽是分别多少cm?
(2)你是否同意小于同学的说法?说明理由.
【分析】(1)设面积为300平方厘米的长方形的长宽分为3x厘米,2x厘米,则3x•2x=300,x2=50,解得x=5,而面积为400平方厘米的正方形的边长为20厘米,由于15>20,所以用一块面积为400平方厘米的正方形纸片,沿着边的方向裁不出一块面积为300平方厘米的长方形纸片,使它的长宽之比为2:3;
(2)根据(1)中的长方形纸片的长和宽即可得出结论.
解:(1)解:设长方形纸片的长为3x(x>0)cm,则宽为2x cm,依题意得,
3x•2x=300,
6x2=300,x2=50,
∵x>0,
∴x==5,
∴长方形纸片的长为15 cm,
答:长方形纸片的长是15cm,宽是10cm;
(2)不同意小于同学的说法.
理由:∵50>49,
∴5 >7,
∴15>21.
∴长方形纸片的长大于20cm,由正方形纸片的面积为400cm2,可知其边长为20cm,
∴长方形纸片的长大于正方形纸片的边长,
∴不能用这块纸片裁出符合要求的长方形纸片.
【点评】本题考查了算术平方根的定义:一个正数的正的平方根叫这个数的算术平方根;0的算术平方根为0.也考查了估算无理数的大小.
三、(本大题共3小题,每小题8分,共24分)
18.我们知道,平方数的开平方运算可以直接求得,如等,有些数则不能直接求得,如,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请你观察下表:
a
…
0.04
4
400
40000
…
…
x
2
y
z
…
(1)表格中的三个值分别为:x= 0.2 ;y= 20 ;z= 200 ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,= 2×10n ;
(3)利用这一规律,解决下面的问题:
已知≈2.358,则①≈ 0.2358 ;②≈ 235.8 .
【分析】(1)利用算术平方根定义计算,填表即可;
(2)归纳总结得到一般性规律,求出的值即可;
(3)利用得出的规律计算即可得到结果.
解:(1)根据题意得:x=0.2;y=20;z=200;
(2)当a=4×100n(n为整数)时,=2×10n;
(3)若≈2.358,则①≈0.2358;②≈235.8.
故答案为:(1)0.2;20;200;(2)2×10n;(3)0.2358;235.8.
【点评】此题考查了算术平方根,熟练掌握算术平方根的定义是解本题的关键.
19.如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(5,3),B(2,1),C(6,﹣2),三角形ABC中任意一点P(x0,y0),经平移后对应点为P'(x0﹣8,y0+2),将三角形ABC作同样的平移得到三角形A'B'C',点A,B,C的对应点分别为A',B',C'.
(1)点A'的坐标为 (﹣3,5) ,点B'的坐标为 (﹣6,3) ;
(2)求出三角形A'B'C'的面积;
(3)点D是x轴上一动点,当S△B'C'D=S△A'B'C'时,请直接写出点D的坐标 或 .
【分析】(1)先确定平移规则,再写根据平移规则求出对应坐标即可;
(2)把三角形的面积看成长方形的面积减去周围的三个三角形面积即可;
(3)设D(m,0),根据面积关系构建方程求解即可.
解:(1)由P(x0,y0)到P'(x0﹣8,y0+2)可知向左平移了8个单位,向上平移了2个单位,
∴A'(5﹣8,3+2),B'(2﹣8,1+2),
即A'(﹣3,5),B'(﹣6,3),
故答案为:(﹣3,5),(﹣6,3);
(2)S△A'B'C′=;
(3)设D(m,0),
由题意,,
∴或,
∴D(,0)或(﹣,0),
故答案为:或.
【点评】本题考查作图﹣平移变换,三角形的面积等知识,掌握平移变换的性质,学会利用参数构建方程是解决问题的关键.
20.如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长是多少?
【分析】(1)易得5个小正方形的面积的和,那么就得到了大正方形的面积,求得面积的算术平方根即可为大正方形的边长;
(2)利用勾股定理得出直角三角形的斜边长,进而得出答案.
(3)一共有10个小正方形,那么组成的大正方形的面积为10,边长为10的算术平方根,进而求出即可.
解:(1)5个小正方形拼成一个大正方形后,面积不变,
所以拼成的正方形的面积是:5×1×1=5,
边长=;
(2)如图所示:
点A表示的数是:;
点A表示的数的相反数是:;
(3)如图所示:
拼成的正方形的面积与原面积相等1×1×10=10,边长为.
【点评】本题考查了正方形的面积和正方形的有关画图,巧妙地根据网格的特点画出正方形是解此题的关键.正方形的面积是由组成正方形的面积的小正方形的个数决定的;边长为面积的算术平方根.
五、(本大题共2小题,每小题9分,共18分)
21.如图,在平面直角坐标系中,1cm对应坐标轴上的1个单位长度,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,以每秒1cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,两点都停止运动.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3s时,求三角形PQC的面积;
(3)设两点运动的时间为ts,当三角形OPQ的面积为16cm2时,求t的值(直接写出答案).
【分析】(1)根据坐标与图形性质求出B,C,D三个点的坐标;
(2)过点P作PM⊥x轴于M,延长BC交x轴于点N,延长DC交PM于点K,根据三角形的面积公式求出三角形PQC的面积;
(3)分0≤t<4、4≤t≤5两种情况,根据三角形的面积公式计算即可.
解:(1)∵AB∥CD∥x轴,BC∥DE∥y轴,AB=CD=4,OA=5,DE=2,
∴B(4,5),C(4,2),D(8,2);
(2)如图1,当P,Q两点运动3s时,点P(3,5),Q(6,0),
过点P作PM⊥x轴于M,延长BC交x轴于点N,延长DC交PM于点K,
则M(3,0),N(4,0),K(3,2),
∴QM=3,CK=MN=1,PK=BC=3,CN=NQ=2,
∴S△PQC=×3×5﹣×1×3﹣×2×2﹣2×1=2;
(3)由题意得,点P运动的路径长为AB+BC=4+3=7,用时需要7秒,
点Q运动的路径长为OE+DE=8+2=10,用时需要5秒,
∵其中一点到达终点时,运动停止,
∴时间t的取值范围为0≤t≤5,
①当0≤t<4时,如图2,OA=5,OQ=2t,
则×2t×5=16,
解得:t=3.2;
②当4≤t≤5时,如图3,过点P作PM⊥ED,交ED的延长线于M,
则OE=8,EM=9﹣t,PM=4,EQ=2t﹣8,MQ=17﹣3t,
则×(4+8)×(9﹣t)﹣×4×(17﹣3t)﹣×8×(2t﹣8)=16,
解得:t=4.5
综上所述,三角形OPQ的面积为16cm2时,t=3.2或t=4.5.
【点评】本题考查的是三角形的面积计算,灵活运用分情况讨论思想、熟记三角形的面积公式是解题的关键.
22.如图所示,A(1,0),点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,点C的坐标为(a,b),且.
(1)直接写出点C的坐标 (﹣3,2) ;
(2)直接写出点E的坐标 (﹣2,0) ;
(3)点P是直线CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
【分析】(1)直接利用算术平方根的性质得出a,b的值,即可得出答案;
(2)利用平移的性质得出点E的坐标;
(3)分三种情况讨论:①当点P在线段EC上时:如图,过点P作PN∥CB,②当点P在线段EC的延长线上时,如图,过点P作PN∥CB,③当点P在线段CE的延长线上时,再利用平行线的性质分析得出答案.
解:(1)∵
∴a+3=0,b﹣2=0,解得:a=﹣3,b=2,
∵点C的坐标为(a,b),
∴点C的坐标为:(﹣3,2);
(2)∵点B在y轴上,点C的坐标为:(﹣3,2),
∴B点向左平移了3个单位长度,
∴A(1,0),向左平移3个单位得到:(﹣2,0),
∴点E的坐标为:(﹣2,0);
(3)①当点P在线段EC上时:
如图,过点P作PN∥CB,
∴∠CBP=∠BPN,
又∵BC∥AE,
∴PN∥AE,
∴∠EAP=∠APN,
∴∠CBP+∠EAP=∠BPN+∠APN=∠APB,即z=x+y.
②当点P在线段EC的延长线上时,
如图,过点P作PN∥CB,
∴∠CBP=∠BPN,
又∵BC∥AE,
∴PN∥AE,
∴∠EAP=∠APN,
∴∠EAP﹣∠CBP=∠APN﹣∠BPN=∠APB,即z=y﹣x.
③当点P在线段CE的延长线上时,
如图,过点P作PN∥CB,
∴∠CBP=∠BPN,
又∵BC∥AE,
∴PN∥AE,
∴∠EAP=∠APN,
∴∠CBP﹣∠DAP=∠BPN﹣∠APN=∠APB,即z=x﹣y.
【点评】此题主要考查了平移的性质以及平行线的性质,算术平方根的非负性的应用,坐标与图形,清晰的分类讨论是解题关键.
六、(本大题共1小题,共12分)
23.为了保障学生安全,学校在操场两侧各安装了一枚探照灯,便于夜间对整个校园进行巡视.如图1,操场两侧MN∥PQ,且测得∠BAQ=45°.灯A射线自AP顺时针转至AQ便立即回转,灯B射线自BN顺时针转至BM便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,若灯B转动的速度是b°/秒,且a,b满足+|2b﹣4|=0.
(1)求a,b的值.
(2)若灯B射线先转动5秒,灯A射线才开始转动,在灯B射线与AB重合之前,灯A转动几秒,可以使两灯射线平行?(3)如图2,两灯同时转动,在灯B射线到达BM之前,若射出的光束交于点C,作∠NBC的角平分线交AC的延长线于点D.若t秒后,为定值,请你直接写出t的取值范围 45<t<60 .
【分析】(1)根据≥0,|a|≥0即可;
(2)根据已知条件表示出角度,再根据两直线平行的性质,列方程即可求解;
(3)通过计算,灯A射线与AB重合,灯A射线与AQ重合分别求出t的值,即可确定满足条件的t取值范围.
解:
(1)∵+|2b﹣4|=0,
∴,|2b﹣4|=0,
∴a=3,b=2.
(2)如图1所示:
∵灯B转动的速度是2°/秒,
∴先转动5秒也即先转动10°,
∵∠BAQ=45°,
∴灯A转动x秒后,∠MAB=180°﹣45°﹣3x,
∠ABQ=180°﹣45°﹣2x﹣10°,
当两灯射线平行时,则MA∥BQ,
∴∠MAB=∠ABQ,
即180°﹣45°﹣3x=180°﹣45°﹣2x﹣10°,
解得x=10(秒),
∴灯A转动10秒,可以使两灯射线平行.
(3)如图2所示:
经过t秒,
当灯A射线与AB重合时,3t=135°,
∴t=45,
当灯A射线到达AQ时,3t=180°,
∴t=60,
当45<t<60时,
根据题意得:∠NBC=2t,∠PAC=3t,
∵BD平分∠NBC,
∴∠NBD=t,
∵∠BAC=∠PAC﹣∠PAB=3t﹣135°,
∴∠D=180°﹣∠DBA﹣∠BAC=180°﹣(135°﹣t)﹣(3t﹣135°)=180°﹣2t,
∵∠BAC=3t﹣135°,
∴=90°﹣t+t﹣45°=45°.
∴当灯A射线返回AP时,灯B射线与AB重合前,
∠BAC=45°﹣(3t﹣180°)=225°﹣3t,
∠DBA=135°﹣t,
∠D=180°﹣∠BAC﹣∠DBA=4t﹣180°,
=2t﹣90°+75°﹣t=t﹣15°,不是定值,
∴为定值,t的取值范围是45<t<60,
故答案为:45<t<60.
【点评】本题考查了平行线的性质,理解两灯的旋转过程以及表示出相应角度是解决本题的关键.
相关试卷
这是一份2022-2023学年江西省南昌市南昌县八年级(下)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年江西省南昌市南昌县七年级(下)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年江西省南昌市南昌县七年级(下)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。









