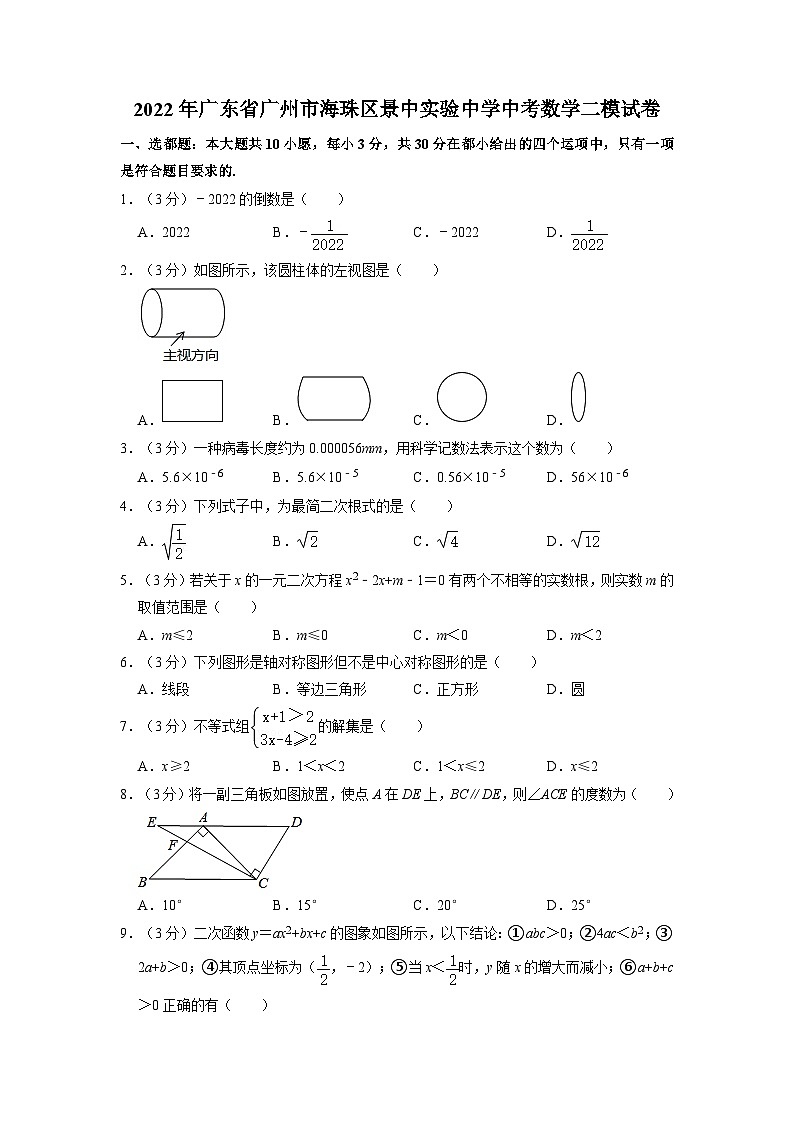
2022年广东省广州市海珠区景中实验中学中考数学二模试卷

这是一份2022年广东省广州市海珠区景中实验中学中考数学二模试卷，共17页。试卷主要包含了选都题，填空厦，解答题等内容，欢迎下载使用。

2022年广东省广州市海珠区景中实验中学中考数学二模试卷
一、选都题：本大题共10小愿，每小3分，共30分在都小给出的四个运项中，只有一项是符合题目要求的.
1．（3分）﹣2022的倒数是（　　）
A．2022 B．﹣ C．﹣2022 D．
2．（3分）如图所示，该圆柱体的左视图是（　　）

A． B． C． D．
3．（3分）一种病毒长度约为0.000056mm，用科学记数法表示这个数为（　　）
A．5.6×10﹣6 B．5.6×10﹣5 C．0.56×10﹣5 D．56×10﹣6
4．（3分）下列式子中，为最简二次根式的是（　　）
A． B． C． D．
5．（3分）若关于x的一元二次方程x2﹣2x+m﹣1＝0有两个不相等的实数根，则实数m的取值范围是（　　）
A．m≤2 B．m≤0 C．m＜0 D．m＜2
6．（3分）下列图形是轴对称图形但不是中心对称图形的是（　　）
A．线段 B．等边三角形 C．正方形 D．圆
7．（3分）不等式组的解集是（　　）
A．x≥2 B．1＜x＜2 C．1＜x≤2 D．x≤2
8．（3分）将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为（　　）

A．10° B．15° C．20° D．25°
9．（3分）二次函数y＝ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④其顶点坐标为（，﹣2）；⑤当x＜时，y随x的增大而减小；⑥a+b+c＞0正确的有（　　）

A．3个 B．4个 C．5个 D．6个
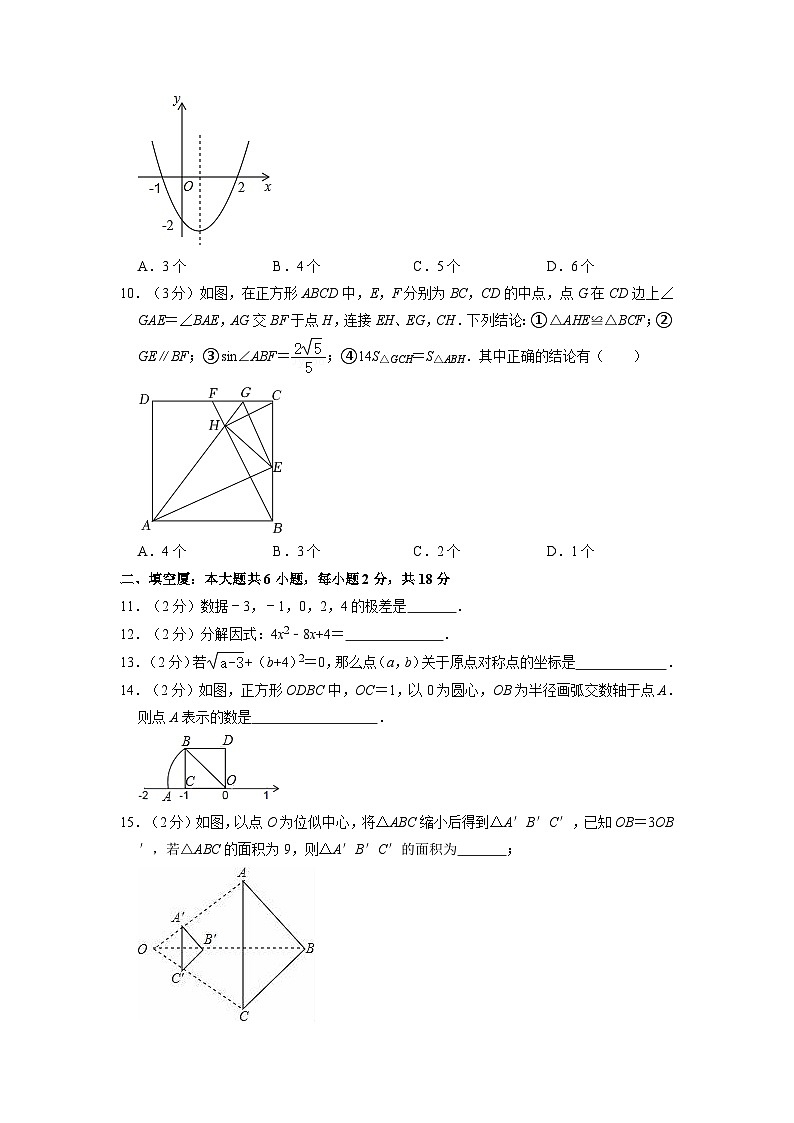
10．（3分）如图，在正方形ABCD中，E，F分别为BC，CD的中点，点G在CD边上∠GAE＝∠BAE，AG交BF于点H，连接EH、EG，CH．下列结论：①△AHE≌△BCF；②GE∥BF；③sin∠ABF＝；④14S△GCH＝S△ABH．其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
二、填空厦：本大题共6小题，每小题2分，共18分
11．（2分）数据﹣3，﹣1，0，2，4的极差是　 　．
12．（2分）分解因式：4x2﹣8x+4＝　 　．
13．（2分）若+（b+4）2＝0，那么点（a，b）关于原点对称点的坐标是　 　．
14．（2分）如图，正方形ODBC中，OC＝1，以0为圆心，OB为半径画弧交数轴于点A．则点A表示的数是　 　．

15．（2分）如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知OB＝3OB′，若△ABC的面积为9，则△A′B′C′的面积为　 　；

16．（2分）如图，在⊙O中，AB是⊙O的直径，AB＝2，AD＝BC，AD，BC交于点E，点D为的中点，点G为平面内一动点，且BG⊥EG，则AG的最小值为 　 　．

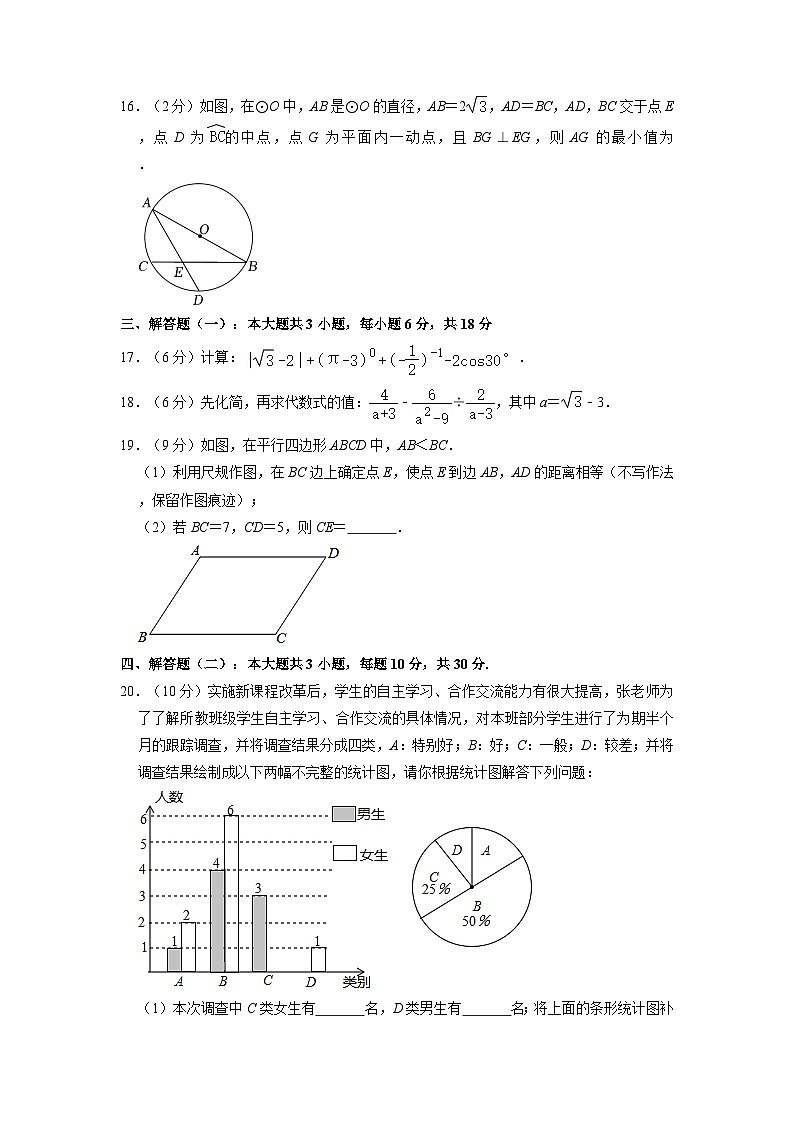
三、解答题（一）：本大题共3小题，每小题6分，共18分
17．（6分）计算：．
18．（6分）先化简，再求代数式的值：﹣÷，其中a＝﹣3．
19．（9分）如图，在平行四边形ABCD中，AB＜BC．
（1）利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；
（2）若BC＝7，CD＝5，则CE＝　 　．

四、解答题（二）：本大题共3小题，每题10分，共30分.
20．（10分）实施新课程改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调查，并将调查结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

（1）本次调查中C类女生有　 　名，D类男生有　 　名；将上面的条形统计图补充完整；
（2）计算扇形统计图中D所占的圆心角是　 　；
（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
21．（10分）火车站北广场将于2016年底投入使用，计划在广场内种植A、B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵．
（1）A、B两种花木的数量分别是多少棵？
（2）如果园林处安排25人同时种植这两种花木，每人每天能种植A花木70棵或B花木60棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？
22．（10分）C919大型客机首飞成功，激发了同学们对航空科技的兴趣．如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB∥CD，AM∥BN∥ED，AE⊥DE，其中AB＝17cm，ED＝25cm，求出线段BE和CD的长．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，结果保留小数点后两位）

五、解答题（三）：本大题共2小题，每题12分，共24分.
23．（12分）如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．
（1）求证：DP∥AB；
（2）试猜想线段AE，EF，BF之间有何数量关系，并加以证明；
（3）若AC＝6，BC＝8，求线段PD的长．

24．（12分）如图，抛物线y＝ax2+bx+c经过点A（﹣2，5），与x轴相交于B（﹣1，0），C（3，0）两点．
（1）求抛物线的函数表达式；
（2）点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC'D，若点C'恰好落在抛物线的对称轴上，求点C'和点D的坐标；
（3）设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△CPQ为等边三角形时，求直线BP的函数表达式．


2022年广东省广州市海珠区景中实验中学中考数学二模试卷
参考答案与试题解析
一、选都题：本大题共10小愿，每小3分，共30分在都小给出的四个运项中，只有一项是符合题目要求的.
1． 解：﹣2022的倒数是：﹣．
故选：B．
2． 解：该圆柱体的左视图是：

故选：C．
3． 解：0.000056＝5.6×10﹣5．
故选：B．
4． 解：A、原式＝，不符合题意；
B、是最简二次根式，符合题意；
C、原式＝2，不符合题意；
D、原式＝2，不符合题意；
故选：B．
5． 解：∵关于x的一元二次方程x2﹣2x+m﹣1＝0有两个不相等的实数根，
∴Δ＝（﹣2）2﹣4×1×（m﹣1）＝8﹣4m＞0，
∴m＜2．
故选：D．
6． 解：A、线段，是轴对称图形，也是中心对称图形，故本选项不符合题意；
B、等边三角形，是轴对称图形但不是中心对称图形，故本选项符合题意；
C、正方形，是轴对称图形，也是中心对称图形，故本选项不符合题意；
D、圆，是轴对称图形，也是中心对称图形，故本选项不符合题意．
故选：B．
7． 解：由x+1＞2，得：x＞1，
由3x﹣4≥2，得：x≥2，
则不等式组的解集为x≥2，
故选：A．
8． 解：∵BC∥DE，
∴∠BCE＝∠E＝30°，
∴∠ACE＝∠ACB﹣∠BCE＝45°﹣30°＝15°，
故选：B．
9． 解：由图象可知，
抛物线开口向上，则a＞0，顶点在y轴右侧，则b＜0，与y轴交于负半轴，则c＜0，
∴abc＞0，故①正确，
函数图象与x轴有两个不同的交点，则b2﹣4ac＞0，即4ac＜b2，故②正确，
由图象可知，，则2b＝﹣2a，2a+b＝﹣b＞0，故③正确，
由抛物线过点（﹣1，0），（0，﹣2），（2，0），可得，
，
得，
∴y＝x2﹣x﹣2＝，
∴顶点坐标是（，﹣），故④错误，
∴当x＜时，y随x的增大而减小，故⑤正确，
当x＝1时，y＝a+b+c＜0，故⑥错误，
由上可得，正确是①②③⑤，
故选：B．
10． 解：如图，设BF与AE的交点为O，

设AB＝4a，
∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD＝4a，∠ABC＝∠BCD＝90°，
∵E，F分别为BC，CD的中点，
∴CF＝DF＝2a＝CE＝BE，
∴△ABE≌△BCF（SAS），
∴∠BAE＝∠CBF，BF＝AE，∠AEB＝∠BFC，
∵∠ABF+∠CBF＝90°＝∠ABF+∠BAE，
∴∠AOB＝90°＝∠AOH，
又∵∠BAE＝∠GAE，AO＝AO，
∴△AOH≌△AOB（ASA），
∴AH＝AB，BE＝EH，∠ABE＝∠AHE＝90°，
∴∠AHE＝∠BCF＝90°，AH＝AB＝BC，∠GAE＝∠BAE＝∠BCF，
∴△AHE≌△BCF（AAS），故①正确；
∵AH＝AB，
∴∠AHB＝∠ABH，
∵AB∥CD，
∴∠ABF＝∠CFB，
∴∠CFB＝∠AHB＝∠CHF，
∴FG＝GH，
∵HE＝BE＝CE，
∴∠BHC＝90°，
∴∠GHC＝∠GCH，
∴CG＝GH，
∴FG＝GC＝GH＝a，
又∵CE＝BE，
∴GE∥BF，故②正确；
∵BF＝＝＝2a，
∴sin∠ABF＝sin∠BFC＝＝＝，故③正确；
∵∠CHF＝∠BCF＝90°，∠CFH＝∠CFB，
∴△CFH∽△BFC，
∴，
∴＝，
∴CH＝a，FH＝a，
∴BH＝a，
∵sin∠ABF＝，
∴AO＝a，
∵FG＝GC，
∴S△GCH＝S△FCH＝××a×a＝a2，
∵S△ABH＝×AO×BH＝×a×a＝a2，
∴16S△GCH＝S△ABH＝，故④错误，
故选：B．
二、填空厦：本大题共6小题，每小题2分，共18分
11． 解：由题意可知，极差为4﹣（﹣3）＝7．
故答案为：7．
12． 解：4x2﹣8x+4＝4（x2﹣2x+1）＝4（x﹣1）2．
故答案为：4（x﹣1）2．
13． 解：∵+（b+4）2＝0，
∴a﹣3＝0，b+4＝0，
解得：a＝3，b＝﹣4，
∴点（a，b）的坐标为（3，﹣4），
∴关于原点对称点的坐标是（﹣3，4），
故答案为：（﹣3，4）；
14． 解：数轴上正方形的对角线长为：，
由图中可知O和A之间的距为，
∴点A表示的数是．
15． 解：∵OB＝3OB′，
∴＝，
∵以点O为位似中心，将△ABC缩小后得到△A′B′C′，
∴△A′B′C′∽△ABC，
∴＝．
∴＝，
∵△ABC的面积为9，
∴△A′B′C′的面积为：1．
故答案为：1．
16． 解：连接AC、BD，以BE为直径作⊙M，
∵BG⊥EG，即∠BGE＝90°，
∴点G在⊙M上，
连接AM，当AM与⊙M交于点G时，此时AG最短，如图，

∵AD＝BC，
∴，
∵点D为的中点，
∴，
∴∠CBD＝∠CBA＝∠BAD＝∠CAD，
∴AE＝BE，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠CAD+∠BAD+∠ABC＝90°，
∴∠CBD＝∠CBA＝∠BAD＝∠CAD＝30°，
∴AC＝AB＝＝，
∴BE＝AE＝＝2，
CE＝AE＝1，
∵MG＝MB＝ME＝＝1，
∴CM＝CE+ME＝2，
∴AM＝．
∴AG＝AM﹣MG＝﹣1，
即AG的最小值为﹣1．
故答案为：﹣1．
三、解答题（一）：本大题共3小题，每小题6分，共18分
17． 解：原式＝2﹣+1﹣2﹣2×，
＝2﹣+1﹣2﹣，
＝1﹣2．
18． 解：原式＝﹣•＝﹣＝，
当a＝﹣3时，原式＝＝．
19． 解：（1）如图，点E为所作；

（2）∵点E到边AB，AD的距离相等，
∴AE平分∠BAD，
∴∠BAE＝∠DAE，
∵四边形ABCD为平行四边形，
∴AB＝CD＝5，AD∥BC，
∴∠DAE＝∠AEB，
∴∠BAE＝∠AEB，
∴BE＝BA＝5，
∴CE＝BC﹣BE＝7﹣5＝2．
故答案为2．
四、解答题（二）：本大题共3小题，每题10分，共30分.
20． 解：（1）本次调查的总人数为（6+4）÷50%＝20（人），
∴本次调查中C类女生有20×25%﹣3＝2，
D类男生有20﹣（1+2+6+4+3+1+2）＝1，
补全图形如下：

故答案为：2、1；

（2）扇形统计图中D所占的圆心角是360°×＝36°，
故答案为：36°；

（3）画树状图得：

∵共有6种等可能的结果，所选两位同学恰好是一位男同学和一位女同学的有3种情况，
∴所选两位同学恰好是一位男同学和一位女同学的概率是．
21． 解：（1）设A种花木的数量为x棵，B种花木的数量为y棵，
由题意得：，
解得：，
答：A种花木的数量为4200棵，B种花木的数量为2400棵；

（2）设安排a人种植A花木，由题意得：＝，
解得：a＝15，
经检验：a＝15是原分式方程的解，
25﹣a＝25﹣15＝10，
答：应安排15人种植A花木和10人种植B花木，才能确保同时完成各自的任务．
22． 解：延长DC交BN于点G，交AM于点F，

由题意得：
∠BNC＝∠AFC＝90°，AE＝DF，BE＝GD，AF＝BG＝ED＝25cm，
在Rt△BND中，∠NBD＝37°，
∴ND＝BN•tan37°≈25×0.75＝18.75（cm），
∴BE＝ND＝18.75cm，
∵AB＝17cm，
∴DF＝AE＝AB+BE＝17+18.75＝35.75（cm），
在Rt△AFG中，∠FAC＝45°，
∴FC＝AF•tan45°＝25（cm），
∴CD＝DF﹣FC＝35.75﹣25＝10.75（cm），
∴线段BE的长约为18.75cm，CD的长约为10.75cm．

五、解答题（三）：本大题共2小题，每题12分，共24分.
23． （1）证明：连接OD，如图，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∵∠ACB的平分线交⊙O于点D，
∴∠ACD＝∠BCD＝45°，
∴∠DAB＝∠ABD＝45°，
∴△DAB为等腰直角三角形，
∴DO⊥AB，
∵PD为⊙O的切线，
∴OD⊥PD，
∴DP∥AB；

（2）答：BF﹣AE＝EF，证明如下：
∵AB是⊙O的直径，
∴∠ADB＝∠ADE+∠BDF＝90°，
∵AE⊥CD，BF⊥CD，
∴∠AED＝∠BFD＝90°，
∴∠FBD+∠BDF＝90°，
∴∠FBD＝∠ADE，
∵∠AOD＝∠BOD，
∴AD＝BD，
在△ADE和△DBF中

∴△ADE≌△DBF（AAS），
∴BF＝DE，AE＝DF，
∴BF﹣AE＝DE﹣DF，
即BF﹣AE＝EF．
[问题二法2：∠ACD＝∠CAE＝45°，所以AE＝CE，∠DCB＝∠FBC＝45°，所以BF＝CF，CF＝CE+EF＝AE+EF 所以AE+FE＝BF]
（3）解：在Rt△ACB中，AB＝＝10，
∵△DAB为等腰直角三角形，
∴AD＝＝＝5，
∵AE⊥CD，
∴△ACE为等腰直角三角形，
∴AE＝CE＝＝＝3，
在Rt△AED中，DE＝＝＝4，
∴CD＝CE+DE＝3+4＝7，
∵∠PDA＝∠PCD，∠P＝∠P，
∴△PDA∽△PCD，
∴＝＝＝，
∴PA＝PD，PC＝PD，
而PC＝PA+AC，
∴PD+6＝PD，
∴PD＝．

24． 解：（1）由题意得：
解得，
∴抛物线的函数表达式为y＝x2﹣2x﹣3．
（2）∵抛物线与x轴交于B（﹣1，0），C（3，0），
∴BC＝4，抛物线的对称轴为直线x＝1，
如图，设抛物线的对称轴与x轴交于点H，则H点的坐标为（1，0），BH＝2，
由翻折得C′B＝CB＝4，
在Rt△BHC′中，由勾股定理，得C′H＝＝＝2，
∴点C′的坐标为（1，2），tan∠C′BH＝，
∴∠C′BH＝60°，
由翻折得∠DBH＝∠C′BH＝30°，
在Rt△BHD中，DH＝BH•tan∠DBH＝2•tan30°＝，
∴点D的坐标为（1，）．
（3）解：取（2）中的点C′，D，连接CC′，

∵BC′＝BC，∠C′BC＝60°，
∴△C′CB为等边三角形．分类讨论如下：
①当点P在x轴的上方时，点Q在x轴上方，连接BQ，C′P．
∵△PCQ，△C′CB为等边三角形，
∴CQ＝CP，BC＝C′C，∠PCQ＝∠C′CB＝60°，
∴∠BCQ＝∠C′CP，
∴△BCQ≌△C′CP（SAS），
∴BQ＝C′P．
∵点Q在抛物线的对称轴上，
∴BQ＝CQ，
∴C′P＝CQ＝CP，
又∵BC′＝BC，
∴BP垂直平分CC′，
由翻折可知BD垂直平分CC′，
∴点D在直线BP上，
设直线BP的函数表达式为y＝kx+b1，
则，解得，
∴直线BP的函数表达式为y＝．
②当点P在x轴的下方时，点Q在x轴下方．

∵△PCQ，△C′CB为等边三角形，
∴CP＝CQ，BC＝CC′，∠CC′B＝∠QCP＝∠C′CB＝60°．
∴∠BCP＝∠C′CQ，
∴△BCP≌△C′CQ（SAS），
∴∠CBP＝∠CC′Q，
∵BC′＝CC′，C′H⊥BC，
∴∠CC′Q＝∠CC′B＝30°．
∴∠CBP＝30°，
设BP与y轴相交于点E，
在Rt△BOE中，OE＝OB•tan∠CBP＝OB•tan30°＝1×，
∴点E的坐标为（0，﹣）．
设直线BP的函数表达式为y＝mx+n，
则，解得，
∴直线BP的函数表达式为y＝﹣．
综上所述，直线BP的函数表达式为y＝或y＝﹣．