广西玉林市北流市2023届高三年级教学质量检测数学（理）试题 附答案

2023年5月北流市高三年级教学质量检测

数学试题（理科）

注意事项

1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上．

2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．

3．考试结束后，将本试卷和答题卡一并交回．

第I卷（选择题共60分）

一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知集合，，则（    ）

A． B． C． D．

2．已知，为虚数单位，若为实数，则（    ）

A．3 B． C． D．

3．已知平面向量，，且，（    ）

A．14 B．1 C． D．

4．大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论．主要用于解释中国传统文化中的太极衍生原理．大衍数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中华传统文化中隐藏着的世界数学史上第一道数列题．其前10项依次是0，2，4，8，12，18，24，32，40，50，，则这个数列的第20项为（    ）

A．204 B．202 C．200 D．198

5．已知抛物线：焦点为，准线为，点在上，直线与交于点，则（    ）

A． B． C．2 D．1

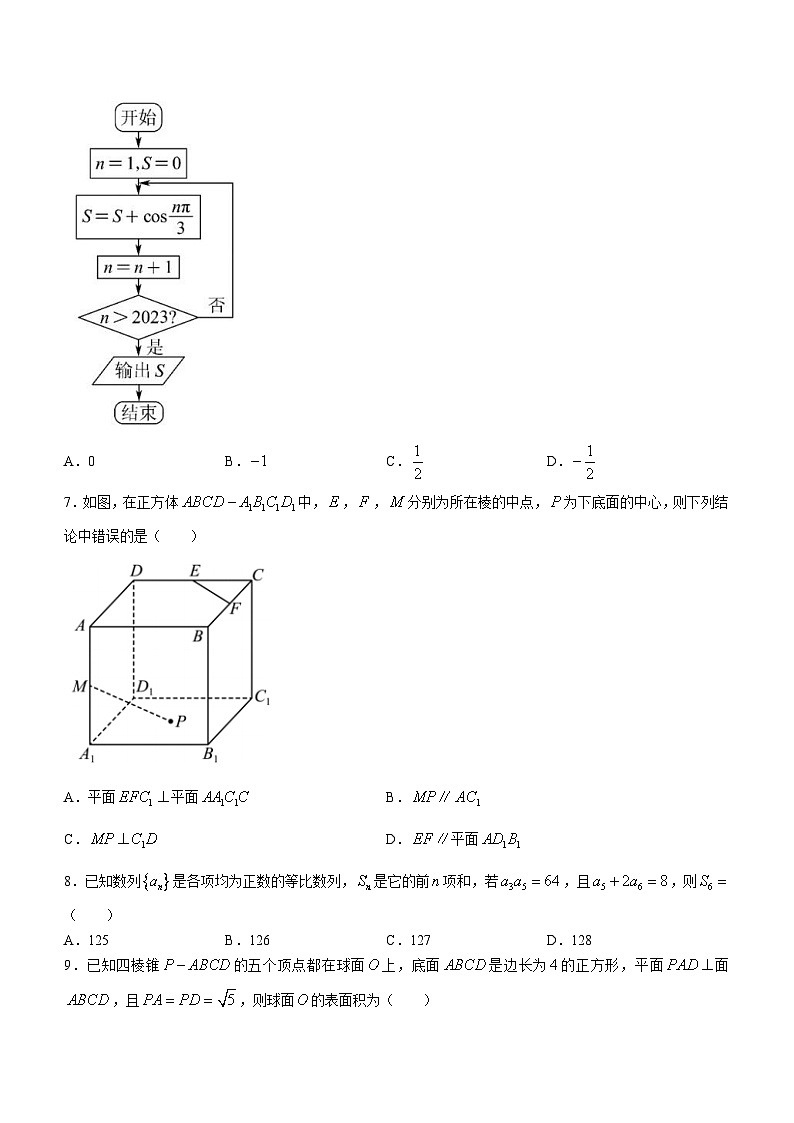
6．执行如图的程序框图，输出的值是（    ）

A．0 B． C． D．

7．如图，在正方体中，，，分别为所在棱的中点，为下底面的中心，则下列结论中错误的是（    ）

A．平面平面 B．

C．  D．平面

8．已知数列是各项均为正数的等比数列，是它的前项和，若，且，则（    ）

A．125 B．126 C．127 D．128

9．已知四棱锥的五个顶点都在球面上，底面是边长为的正方形，平面面，且，则球面的表面积为（    ）

A． B． C． D．

10．为弘扬传统文化，某校进行了书法大赛，同学们踊跃报名，在成绩公布之前，可以确定甲、乙、丙、丁、戊5名从小就练习书法的同学锁定了第1至5名．甲和乙去询问成绩，组委会对甲说：“很遗憾，你和乙都没有获得冠军．”对乙说：“你当然不会是五人中最差的．”则最终丙和丁获得前两名的概率为（    ）

A． B． C． D．

11．双曲线：的左焦点和虚轴的一个端点分别为，，点为右支上一动点，若周长的最小值为，则的离心率为（    ）

A． B． C． D．

12．已知函数，的定义域均为，是奇函数，且，，则（    ）

A．为奇函数 B．为奇函数 C． D．

第II卷（非选择题共90分）

二、填空题：本题共4小题，每小题5分，共20分．

13．2022年卡塔尔世界杯期间，3男3女共6位球迷赛后在比赛场地站成一排合影留念，则男、女球迷相间排列的概率为________．

14．写出一个半径为1且与圆：及直线：都相切的圆的方程________．

15．已知为奇函数，若对任意，存在满足，则实数的取值范围是________．

16．已知函数（为常数）有两个极值点：，，若恒成立，则实数的取值范围是________．

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．

（一）必考题：共60分．

17．（12分）在中，角，，所对的边分别，，，且．

（1）求角的值；

（2）已知在边上，且，，求的面积的最大值．

18．（12分）如图，在四棱锥中，为等边三角形，，，且，平面底面．

（1）证明：平面；

（2）点为棱的中点，求二面角的正弦值．

19．（12分）随着蓉城生态公园绿道全环贯通，环城绿道骑行成为最热门的户外休闲方式之一．环城绿道全程约100公里，不仅可以绕蓉城一圈，更能360度无死角欣赏蓉城这座城市的发展与魅力．某位同学近半年来骑行了5次，各次骑行期间的身体综合指标评分与对应用时（单位：小时）如下表：

（1）由上表数据看出，可用线性回归模型拟合与的关系，请用相关系数加以说明；

（2）建立关于的回归方程．

参考数据和参考公式：

相关系数，，，．

20．（12分）已知椭圆：的离心率为，、分别是其左、右焦点，若是椭圆上的右顶点，且．

（1）求椭圆的方程；

（2）设直线与椭圆交于、两点，点关于轴的对称点为（与不重合），问直线与轴是否交于一个定点？若是，请写出该定点的坐标，并证明你的结论；若不是，请说明理由．

21．（12分）已知函数，，且曲线在点处的切线斜率均不小于2．

（1）求的值；

（2）求证：函数在区间内存在唯一的零点．

（二）选考题：共10分，请考生在22、23题中任选一题作答．如果多做，则按所做的第一题计分．

22．【选修4-4：坐标系与参数方程】（10分）

在直角坐标系中，已知曲线：（为参数，），在极坐标系中，曲线是以为圆心且过极点的圆．

（1）分别写出曲线普通方程和曲线的极坐标方程；

（2）直线：与曲线、分别交于、两点（异于极点），求．

23．【选修4-5：不等式选讲】（10分）

已知函数，．

（1）若，求不等式的解集；

（2）已知，若对任意，都存在，使得，求实数的取值范围．

2023年5月北流市高三教学质量检测

数学参考答案（理科）

1-5：ACACD 6-10：CCBAD 11-12：BD

1．【答案】A  【解析】，解得，所以，由于，所以．故选：A

2．【答案】C【解析】因为为实数，则，即，所以．故选：C．

3．【答案】A  【解析】因为，，，所以，

所以．故选A．

4．【答案】C  【解析】由数列前10项的规律可知：当为偶数时，；

当为奇数时，，所以，故选：C．

5．【答案】D  【解析】由在上，有，得，

所以，，

过点作的垂线，垂足为，由抛物线的定义可知，设与轴交于点，则，有，又，所以为中点，有，．

故选：D．

6．【答案】C  【解析】根据题中所给的框图，可知输出的的值：

故选：C

7．【答案】C  【解析】对于A选项，由，分别为所在棱的中点得，由正方体的性质易知，平面，平面，所以，，

，，平面，所以平面，平面，

所以平面平面，故A选项正确；

对于B选项，为下底面的中心，故为，的中点，因为为所在棱的中点，所以，故B选项正确；

对于C选项，若，由B选项知，则有，

另一方面，由正方体的性质知为直角三角形，，

所以不满足，故C选项错误；

对于D选项，由A选项知，由正方体的性质易知，

所以，平面，平面，

所以平面，故D选项正确．故选：C．

8．【答案】B  【解析】设等比数列的公比为，且，，

，，

所以，即，故选：B．

9．【答案】A  【解析】如图，取中点为，三角形外接圆圆心为，正方形外接圆圆心为，过，作平面，底面垂线，则两垂线交点为四棱锥外接球球心．因平面平面，平面平面，，

平面，则平面．又平面，则，

因，则四边形为矩形．

设三角形外接圆半径为，则，又，，

则，则，

设外接球半径为，则，又

则，则球表面积为：．故选：A．

10．【答案】D  【解析】由概率的相关性质，只需分析甲乙丙丁戊五人情况即可．

①若甲是最后一名，则乙可能是二、三、四名，剩下三人共有种情况，此时共有种情况；

②若甲不是最后一名，则甲乙需排在二、三、四名，有种情况，剩下三人共有种情况，此时有种情况．

则一共有种不同的名次情况，最终丙和丁获得前两名的情况有种，故丙和丁获得前两名的概率．

11．【答案】B  【解析】解：由题意可得，，设，由双曲线的定义可得，，

，

则的周长为

当且仅当，，共线，取得最小值，且为

由题意可得，

即，

故选：B．

12．【答案】D【解析】因为，所以，

又，则有，因为是奇函数，

所以，

可得，即有与，

即，所以是周期为4的周期函数，

故也是周期为4的周期函数．

因为，所以，所以为偶函数．故A错误；

由是奇函数，则，所以，又，

所以，所以C选项错误；

由得，所以B选项错误；因为，

，

所以，所以，所以D选项正确．故选：D．

13．【答案】  【解析】6位球迷站成一排的不同方法数为，其中男、女球迷相间排列的方法数为，所以所求的概率为．

14．【答案】，，

（答案不唯一，写出一个即可）．

【解析】设所求圆的圆心坐标为，由已知圆与直线：相切，圆与圆相切，

则有

即得或或，

所以所求圆的方程为或或．

15．【答案】  【解析】因为函数为奇函数，

所以．

又，所以，所以．

由，得，

则，，由对任意

存在，满足，则需的取值范围包含．

当时，，要使的取值范围包含，则，所以

16．【答案】

【解析】

若有两个极值点为，，则，是关于的方程的两个不等的正实根．

由，及方程根的情况，得，则，．

又，所以，要使恒成立，只需恒成立．

又

令，则，

当时，，为减函数，

所以当时，．

由题意，要使恒成立，只需满足．

故答案为：．

17．（12分）解：（1）在中因为，

由正弦定理得， 1分

所以 2分

因为，所以．故 3分

又是的内角，所以．从而． 4分

而为的内角，所以． 5分

（2）因为，所以

所以  6分

从而 8分

由基本不等式可得：， 9分

， 10分

当且仅当，时等号成立， 11分

故的面积的最大值为． 12分

18．解：（1），，

， 1分

又平面平面，平面平面，平面， 3分

平面 （4分）

（2）取的中点，连接，，

为等边三角形，且是的中点，

．

又平面平面，平面平面，平面，

平面，

，，

四边形为矩形，又平面

，，两两垂直，

故以为坐标原点，，，分别为，，轴建立如图所示的空间直角坐标系， 6分

，，，，，

则，，．

设平面的法向量为

令，得 9分

设平面的法向量为，

则，令，得 10分

设二面角的大小为，由图可知为锐角，

则 11分

，

二面角的正弦值为． 12分

19．解：（1），， 2分

，，， 4分

， 6分

相关系数近似为，说明与的相关程度相当高，从而可用线性回归模型拟合与的关系； 7分

（2）由（1）中数据，， 9分

， 11分

关于的回归方程为． 12分

20．解：设椭圆的焦距为，因为椭圆：的离心率为，

所以，即， 1分

因为，，，， 2分

所以，

因为，

所以，，，． 3分

所以，椭圆的方程为 4分

【2】解：设，，则，

所以，联立方程

得，，

所以，， 6分

因为直线与椭圆交于、两点，点关于轴的对称点为与不重合，

所以，，即，

所以，，直线的方程为， 7分

令得， 8分

又因为，，

所以 11分

所以，直线与轴交于点 12分

21．【1】，则， 1分

因为曲线在处的切线斜率均不小于2，

所以， 2分

得，

设），则，

令，令， 4分

所以函数在上单调递增，在上单调递减，

则，所以，又，所以； 5分

【2】由（1）知，，所以，

则． 6分

设，则在上恒成立，

所以函数在上单调递增，得，

即在上恒成立，即在上恒成立，

所以．① 9分

设，则在上恒成立，

所以函数在上单调递增，得，

即，得，

当时，，所以②． 11分

由①②得，在上恒成立，

则函数在上单调递增．

又，，

得，所以函数在内有唯一的零点．即证． 12分

22．（1）由曲线：（为参数，，

消去参数，得 1分

所以曲线的直角坐标方程为 3分（不写出具体范围，扣1分）

因为曲线是以为圆心的圆，且过极点，所以圆心为，半径为1，

故的直角坐标方程为：， 4分

即，将代入可得：圆的极坐标方程为 5分

（2）因为曲线的直角坐标方程为．即，

将代入化简可得的极坐标方程为：，

所以的极坐标方程为； 6分

的极坐标方程为； 7分

因为、是直线：与曲线、的两个交点，

不妨设，，

由于：，：，

所以，， 9分

从而． 10分

23．（1）解：当时， 1分

当时，即，

； 2分

当时，即，

； 3分

当时，即，

， 4分

综上可得不等式的解集为． 5分

（2）解：，

当且仅当时取等号，

 6分

又，且，

 8分

当且仅当，即，时等号成立， 9分

所以 10分．