(浙江期末真题精选)09-图形计算100题(提高)2023年六年级下册数学高频易错题(人教版)
展开试卷说明:本试卷试题精选自浙江省各地市2020-2022近三年的六年级期末真题试卷,难易度均衡,适合浙江省各地市和使用人教版教材的六年级学生小升初复习备考使用!
一、图形计算
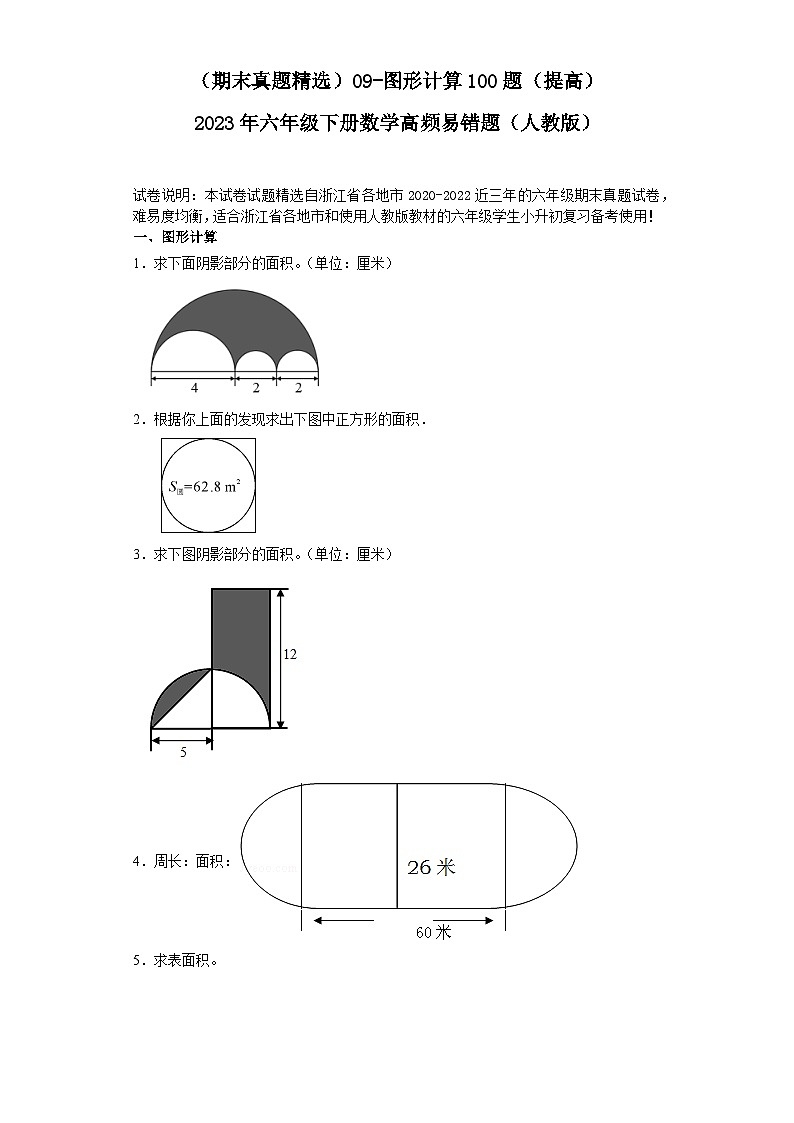
1.求下面阴影部分的面积。(单位:厘米)
2.根据你上面的发现求出下图中正方形的面积.
3.求下图阴影部分的面积。(单位:厘米)
4.周长:面积:
5.求表面积。
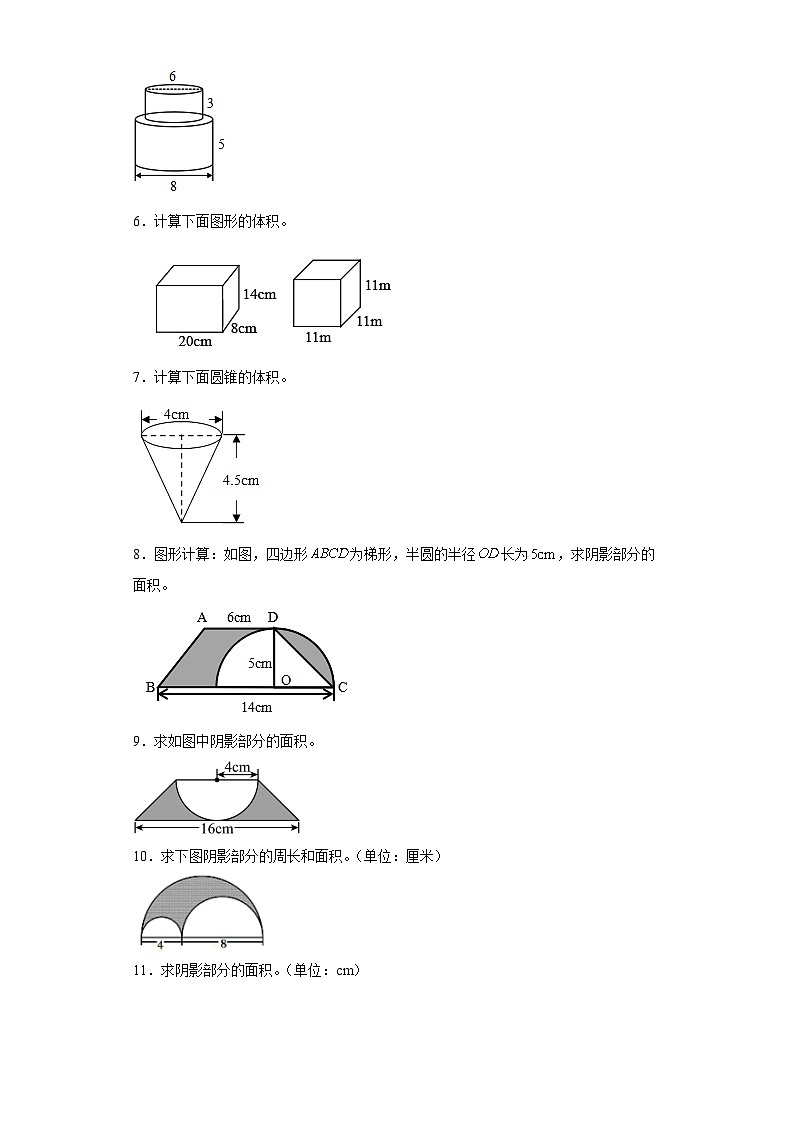
6.计算下面图形的体积。
7.计算下面圆锥的体积。
8.图形计算:如图,四边形为梯形,半圆的半径长为,求阴影部分的面积。
9.求如图中阴影部分的面积。
10.求下图阴影部分的周长和面积。(单位:厘米)
11.求阴影部分的面积。(单位:cm)
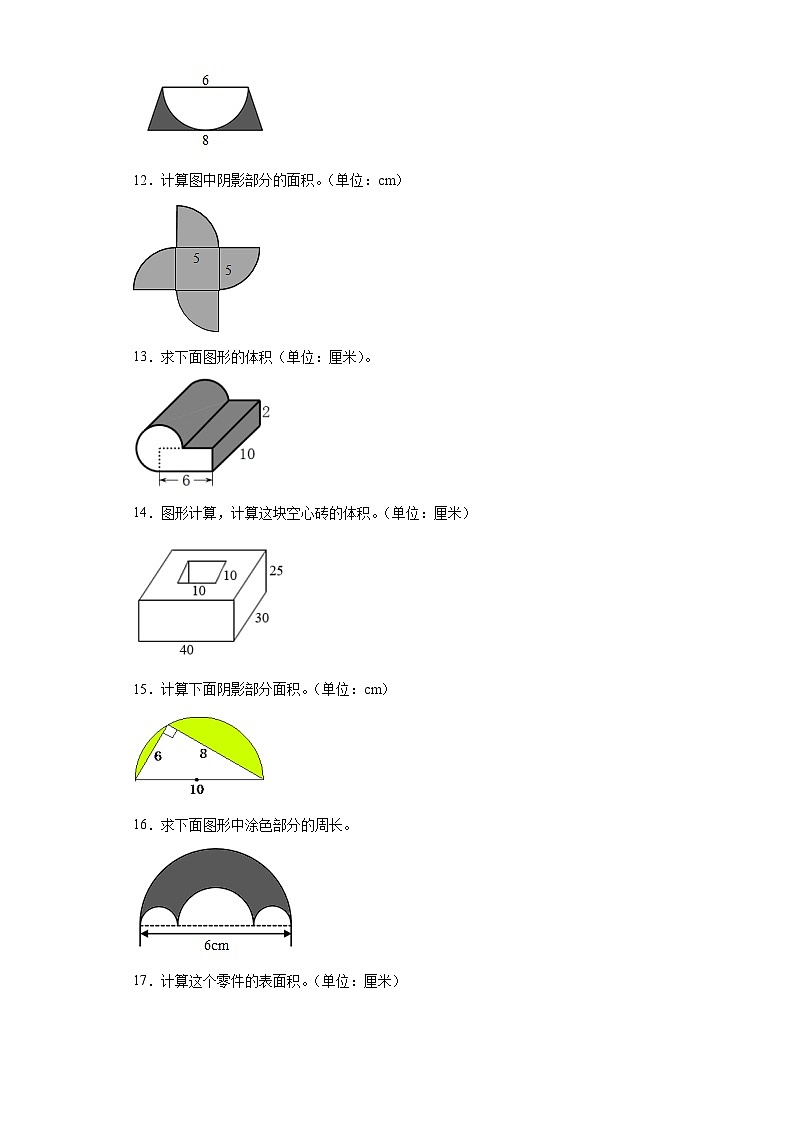
12.计算图中阴影部分的面积。(单位:cm)
13.求下面图形的体积(单位:厘米)。
14.图形计算,计算这块空心砖的体积。(单位:厘米)
15.计算下面阴影部分面积。(单位:cm)
16.求下面图形中涂色部分的周长。
17.计算这个零件的表面积。(单位:厘米)
18.求下图中阴影部分的面积。(单位:厘米)
19.计算下面图形的表面积(单位:厘米)。
20.求下面圆中最大正方形的面积.
21.正方形边长8cm,求阴影部分面积。
22.如图,计算出该图形的表面积和体积。(单位:cm)
23.求表面积和体积(单位:cm)。
24.把如图所示的圆锥从中间切开,下半部分的体积是多少?(单位:厘米)
25.求阴影部分的面积。(单位:厘米;)
26.如图,求下图中阴影部分的面积。(单位:cm)
27.求这个圆柱体的表面积和体积.(单位:厘米)
28.求图中阴影部分的面积.(单位:厘米)
29.计算下面各图形的表面积。(单位:cm)
30.求阴影部分面积:
31.求下面圆柱的表面积.
(1)
(2)
32.求阴影部分面积.
33.求如图阴影部分的面积。(单位:米)
34.求图中阴影部分的面积和周长.
35.求下面图形的表面积。(单位:厘米)
36.(如图)计算正方体的表面积。
37.如图,圆的半径是5厘米,求大、小正方形的面积之差.
38.求下图的体积。
39.求下面图形阴影部分的周长和面积。
40.如图中的圆的周长是18.84厘米,求图中阴影部分的面积.
41.计算下面组合图形的体积(单位:)
42.算出下图中阴影部分的面积。(单位:)
43.求下列图形的表面积和体积.
44.求下图体积。
45.计算下面圆锥的体积。
46.求下面正方体的表面积.
________
47.计算下图阴影部分的面积。
48.图形计算。求图中阴影部分的面积。
49.计算下面圆柱的表面积和体积。(单位:cm)
50.计算下面圆柱的体积(单位cm)。
51.如下图,平行四边形ABCD的面积是400平方厘米,求图中这个圆的面积。
52.如图:长方形ABCD中,AD=15厘米,AB=8厘米.AC、BD是长方形的对角线,求阴影部分的面积.)
53.分别计算下列图形的表面积和体积.(单位:cm)
54.求阴影部分的周长.(单位:cm)
55.观察量杯中水的变化,计算出小正方体的体积。
56.计算圆柱的表面积。
57.下面是一个长方体的展开图,请求出这个长方体的表面积.(单位:cm)
58.求出下图阴影部分的面积。单位:厘米
59.求阴影部分面积(单位:cm)
60.求下列图形的体积。(单位:cm)
61.根据下图中的已知条件,求出图中阴影部分的面积。(单位:厘米)
62.求阴影部分的周长。(单位:cm)
63.计算圆锥的体积.(单位:分米)
64.计算下面各图形的体积。(单位:cm)
65.求下列图形的表面积与体积:
长:4cm 宽:3cm 高:2cm 棱长:5dm.
66.如下图,圆的半径为5cm,三角形的面积为,求阴影部分的面积。
67.计算下面图形中阴影部分的面积。
68.计算下面图形的表面积和体积。(单位:厘米)
69.求下列图中阴影部分的面积。(单位:厘米)
70.计算下面图形阴影部分的面积。
71.求下面圆柱体的侧面积和体积。
72.根据所给数据计算阴影部分的面积。
73.已知下图中,圆的直径是2厘米,求阴影部分的面积.
74.计算下面圆锥的体积。(单位:cm)
75.求下面圆柱和圆锥的体积。(单位:cm)
76.如图所示,阴影甲的面积比阴影乙的面积大54平方厘米,AB=36厘米,CB垂直于AB,求BC的长。(π取3)
77.计算如图形的周长。(单位:米)
78.按要求计算图形的表面积(单位:厘米)。
79.计算下图阴影部分的面积。
80.求图中阴影部分的面积。(单位:厘米)
81.分别算出下列立体图形的表面积和体积。(单位:厘米)
82.求下面圆的周长。
83.求阴影部分面积.(单位:cm)
84.求出阴影部分的面积和周长。
85.看图计算。
体积:
表面积:
86.求下面图形的表面积或体积。
87.求下图中阴影部分的周长和面积。
88.已知S圆=S长方形,求阴影部分的周长和面积
89.已知半圆的半径为4厘米,求阴影部分的面积.
90.求圆柱的表面积?
91.求图中阴影部分的周长和面积.
92.计算下面各图形中阴影部分的面积。(单位:cm)
93.计算下列图形的表面积(单位:分米)。
94.计算下面图形的表面积和体积
95.求下面图形的表面积和体积。(单位:dm)
96.计算下面立体图形的表面积和体积。
97.计算下面图形阴影部分的面积。
(1) (2)
98.求阴影部分的面积。(单位:厘米)
99.求下列图形的周长。
100.单位(厘米)求体积:
求表面积:
参考答案:
1.15.7平方厘米
【分析】阴影部分的面积=半径为4厘米的圆的面积的一半-半径为(4÷2)厘米的圆的面积的一半-半径为(2÷2)厘米的圆的面积的一半-半径为(2÷2)厘米的圆的面积的一半,根据圆的面积公式:S=分别求出这4个半圆的面积,再代入到公式中即可求出阴影部分的面积。
【详解】
=3.14×16÷2
=25.12(平方厘米)
=
=
=6.28(平方厘米)
=
=
=3.14(平方厘米)
25.12-6.28-3.14=15.7(平方厘米)
即阴影部分的面积是15.7平方厘米。
2.80m2
【详解】62.8÷=80(m2)
3.平方厘米
【分析】阴影部分是2个不规则的图形,可以将两个部分拼在一起试试,如图:
这样阴影部分就是一个梯形,求出这个梯形的底和高,就可求出面积。
还可以用图形的总面积减去空白部分的面积。
【详解】将左边的阴影部分移到如图所示的右边,拼成一个梯形,阴影部分的面积就是这个梯形的面积。梯形的上底是长方形的长减去半圆的半径,下底就是长方形的长,高是半圆的半径。所以阴影部分的面积为:
求不规则阴影部分的面积时,可以先试着用割补法,把不规则的图形变成规则的。
4.201.64米,2090.66平方米
【详解】试题分析:分析图形可知,此图的周长是两个60米加上直径为26米的圆(两个半圆合成)的周长;面积是长为60米、宽为26米的长方形面积加上直径为26米的圆的面积,分别计算即可.
解:跑道周长:
3.14×26+60×2,
=81.64+120,
=201.64(米);
运动场面积:
3.14×(26÷2)2+60×26,
=3.14×169+1560,
=530.66+1560,
=2090.66(平方米);
答:这个运动场的跑道的周长是201.64米,面积是2090.66平方米.
点评:分析图形,找出是由哪些图形组合而成,从而寻求解决问题的突破点.
5.282.6
【分析】组合图形的表面积等于两个圆柱表面积之和减去重叠面面积,重叠部分是小圆柱的两个底面面积,也就是说,组合图形的表面积相当于大圆柱的表面积+小圆柱的侧面积。
【详解】3.14×(8÷2)2×2+3.14×8×5
=3.14×16×2+125.6
=100.48+125.6
=226.08
3.14×6×3=56.52
226.08+56.52=282.6
6.2240立方厘米;1331立方米
【分析】根据长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,列式计算即可。
【详解】20×8×14=2240(立方厘米)
11×11×11=1331(立方米)
7.这个圆锥的体积是18.84立方厘米。
【分析】已知圆锥的底面直径和高,利用圆锥的体积V= πr2h , 即可求出这个圆锥的体积。
【详解】×3.14×(4÷2)2×4.5
=3.14×4×1.5
=18.84 (立方厘米)
答:这个圆锥的体积是18.84立方厘米。
8.25平方厘米
【分析】根据图可知:阴影部分面积包括两部分,左边的阴影面积可以用梯形的面积减去空白部分的面积,空白部分的面积包括一个半径为5厘米的圆的面积的四分之一和一个直角边为5厘米的等腰直角三角形的面积,右边阴影部分面积可用半径为5厘米的圆面积的四分之一减去直角边为5厘米的等腰直角三角形的面积,据此代入数据计算即可解答。
【详解】左边阴影部分的面积:
(6+14)×5÷2-3.14×5²÷4-5×5÷2
=50-19.625-12.5
=17.875(平方厘米)
右边阴影部分的面积:
3.14×5²÷4-5×5÷2
=19.625-12.5
=7.125(平方厘米)
阴影部分的总面积:17.875+7.125=25(平方厘米)
答:阴影部分的面积是25平方厘米。
本题主要考查组合图形的面积,熟练找出阴影部分是由哪几部分组成的和或差得到的是解答本题的关键。
9.22.88cm2
【分析】阴影部分的面积=梯形面积-半圆面积,根据梯形面积S=(a+b)h÷2,半圆面积S=πr2÷2,分别代入数据计算即可。
【详解】梯形的面积:
(4×2+16)×4÷2
=(8+16)×4÷2
=24×4÷2
=96÷2
=48(cm2)
半圆的面积:
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(cm2)
阴影部分的面积:
48-25.12=22.88(cm2)
10.37.68厘米;25.12平方厘米
【分析】由图可知,阴影部分的周长=大圆周长的一半+中圆周长的一半+小圆周长的一半,利用“”求出阴影部分的周长;阴影部分的面积=大圆面积的一半-中圆面积的一半-小圆面积的一半,利用“”求出阴影部分的面积,据此解答。
【详解】周长:3.14×(4+8)÷2+3.14×8÷2+3.14×4÷2
=3.14×12÷2+3.14×8÷2+3.14×4÷2
=3.14×(12÷2+8÷2+4÷2)
=3.14×(6+4+2)
=3.14×12
=37.68(厘米)
面积:3.14×[(4+8)÷2]2÷2-3.14×(8÷2)2÷2-3.14×(4÷2)2÷2
=3.14×[12÷2]2÷2-3.14×42÷2-3.14×22÷2
=3.14×62÷2-3.14×42÷2-3.14×22÷2
=113.04÷2-50.24÷2-12.56÷2
=56.52-25.12-6.28
=31.4-6.28
=25.12(平方厘米)
所以,阴影部分的周长是37.68厘米,面积是25.12平方厘米。
11.6.87cm2
【分析】阴影部分的面积=梯形的面积-半圆的面积,,,把图中数据代入公式计算。
【详解】(6+8)×(6÷2)÷2-3.14×(6÷2)2÷2
=14×3÷2-3.14×9÷2
=42÷2-28.26÷2
=21-14.13
=6.87(cm2)
所以,阴影部分的面积是6.87cm2。
12.3.14×52+5×5=103.5(cm2)
【分析】观察图形可知,阴影部分的面积=圆的面积+正方形面积,据此解答即可。
【详解】3.14×52+5×5
=78.5+25
=103.5(cm2)
13.214.2立方厘米
【分析】由图可知,该几何体是由底面圆半径是2厘米,高是10厘米的圆柱的和长10厘米,宽6厘米,高2厘米的长方体组成,根据圆柱的体积公式:,长方体体积公式:,分别求出圆柱和长方体的体积,再将两数相加即可解答。
【详解】22×3.14×10×
=4×3.14×10×
=12.56×10×
=125.6×
=94.2(立方厘米)
10×2×6+94.2
=20×6+94.2
=120+94.2
=214.2(立方厘米)
14.27500立方厘米
【分析】长方体体积=长×宽×高。空心砖的体积用大方体的体积减去小长方体的体积即可。
【详解】40×30×25-10×10×25
=1200×25-100×25
=30000-2500
=27500(立方厘米)
15.15.25cm2
【分析】阴影部分的面积=半圆的面积-三角形的面积,根据半圆的面积=πr2÷2,三角形的面积=底×高÷2,代入数据进行计算即可。
【详解】3.14×(10÷2)2÷2-6×8÷2
=3.14×25÷2-48÷2
=78.5÷2-24
=39.25-24
=15.25(cm2)
阴影部分的面积是15.25cm2。
16.18.84cm
【分析】由图可知,涂色部分的周长=大圆周长的一半+空白部分圆周长的一半,假设空白部分的圆的直径,根据表示出空白部分圆的周长,最后用加法求出涂色部分的周长。
【详解】假设从左往右空白部分圆的直径依次为d1、d2、d3,则d1+d2+d3=6cm。
6×3.14÷2+(3.14d1+3.14d2+3.14d3)÷2
=6×3.14÷2+(d1+d2+d3)×3.14÷2
=6×3.14÷2+6×3.14÷2
=6×3.14÷2×2
=18.84(cm)
所以,涂色部分的周长为18.84cm。
17.260平方厘米
【分析】在长10厘米、宽8厘米、高1厘米的长方体放上一个棱长为4厘米的正方体,则表面积比原来长方体多了4个正方形面,每个正方形的边长是4厘米,根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(10×8+10×1+8×1)×2+4×4×4即可求出这个零件的表面积。
【详解】(10×8+10×1+8×1)×2+4×4×4
=(80+10+8)×2+4×4×4
=98×2+4×4×4
=196+64
=260(平方厘米)
这个零件的表面积是260平方厘米。
18.11.44平方厘米
【分析】由图可知:阴影部分的面积=梯形的面积-半径是4厘米圆的面积的,据此解答即可。
【详解】梯形的面积:
(4+8)×4÷2
=12×4÷2
=48÷2
=24(平方厘米)
扇形的面积:3.14×42×
=3.14×16×
=12.56(平方厘米)
24-12.56=11.44(平方厘米)
19.150平方厘米
【分析】观察图形可知该立体图形的面积等于长方体的表面积加上正方体的表面积再减去两个边长为3的正方形的面积;据此解答。
【详解】8×3×4+3×3×2+3×3×4
=96+18+36
=150(平方厘米)
本题考查了组合图形的表面积,关键是要观察立体图形是由哪几种常规的立体图形构成的,再求它的表面积。
20.3.125平方厘米
【详解】试题分析:用直尺测量圆的直径是2.5厘米,因为正方形是圆内最大的,所以正方形被分为两个相等的直角三角形,根据三角形的面积公式S=ah÷2求出三角形的面积再乘2求出正方形的面积.
解:因为圆的直径是2.5厘米,
所以2.5×(2.5÷2)÷2×2,
=2.5×1.25,
=3.125(平方厘米),
答:圆内最大正方形的面积是3.125平方厘米.
点评:关键是明确把正方形分成两个相等的直角三角形,再利用三角形的面积公式S=ah÷2解决问题.
21.36.48平方厘米
【详解】8÷2=4(厘米)
(3.14×4×4﹣8×4÷2×2)×2
=(3.14×16-32)×2
=(50.24-32)×2
=18.24×2
=36.48(平方厘米)
答:阴影部分面积是36.48平方厘米。
22.1800cm2;4000cm3
【分析】看图,一共有4个小正方体,并且一共有6个面被遮盖住了,所以只要求18个面的面积和。用棱长×棱长×18,即可求出该图形的表面积;
正方体体积=棱长×棱长×棱长,据此先求出1个小正方体的体积,再将其乘4,求出该图形的体积。
【详解】表面积:10×10×18=1800(cm2)
体积:10×10×10×4=4000(cm3)
23.151.62cm2;113.04cm3
【分析】半个圆柱的表面积=圆柱的底面积+圆柱的侧面积的一半+长方形的面积;代入数据计算即可。
根据V柱=πr2h求出圆柱的体积,再除以2就是半个圆柱的体积。
【详解】圆柱的底面积:3.14×2
=3.14×9
=28.26(cm2)
圆柱的侧面积的一半:3.14×6×8÷2=75.36(cm2)
长方形的面积:6×8=48(cm2)
半个圆柱的表面积:28.26+75.36+48=151.62(cm2)
半个圆柱的体积:3.14×2×8÷2
=28.26×8÷2
=226.08÷2
=113.04(cm3)
根据图形特点灵活运用圆柱的表面积公式和体积公式。
24.593.46立方厘米
【分析】先求出上面圆锥的高,下半部分的体积=大圆锥的体积-小圆锥的体积,根据圆锥的体积V=πr2h=Sh,把数值代入公式,依次解答即可。
【详解】18÷2=9(厘米)
×3.14×62×18-×3.14×32×9
=×3.14×36×18-×3.14×9×9
=×113.04×18-×28.26×9
=37.68×18-9.42×9
=678.24-84.78
=593.46(立方厘米)
下半部分的体积是593.46立方厘米。
25.1.14平方厘米
【分析】
如图,把图中阴影部分①和②分别割补到③和④,则阴影部分面积=半径为2厘米的圆的面积-腰为2厘米的等腰直角三角形的面积,根据圆的面积公式:S=πr2,三角形面积公式:S=ab÷2,代入数据即可求解。
【详解】×3.14×22-2×2÷2
=3.14-2
=1.14(平方厘米)
则阴影部分的面积是1.14平方厘米。
26.11.44cm2
【分析】观察图形可知,阴影部分的面积=梯形的面积-圆的面积;根据梯形的面积公式S=(a+b)h÷2,圆的面积公式S=πr2,把数据代入公式求解。
【详解】梯形的面积:
(4+8)×4÷2
=12×4÷2
=24(cm2)
圆的面积:
3.14×42×
=3.14×16×
=3.14×4
=12.56(cm2)
阴影部分的面积:
24-12.56=11.44(cm2)
阴影部分的面积是11.44cm2。
27.表面积:100.48平方厘米 体积:75.36立方厘米
【详解】表面积:2×3.14×(4÷2)2=25.12(平方厘米)
3.14×4×6=75.36(平方厘米)
25.12+75.36=100.48(平方厘米)
体积:3.14×(4÷2)2×6=75.36(立方厘米)
28.74.88平方厘米.
【详解】试题分析:我们运用梯形的面积公减去半圆的面积,就是阴影部分的面积,梯形的面积公式=(上底+下底)×高÷2,
半圆的面积=圆的面积÷2.
解:(10+15)×8÷2﹣3.14×(8÷2)2÷2,
=25×8÷2﹣3.14×8,
=100﹣25.12,
=74.88(平方厘米);
答:阴影部分的面积是74.88平方厘米.
点评:本题主要考查了梯形的面积公式及圆的面积公式的运用情况,同时考查了学生的计算能力.
29.600cm;432cm;87.92cm
【分析】(1)正方体的表面积=棱长×棱长×6。
(2)长方体的表面积=(长×宽+宽×高+长×高)×2。
(3)圆柱的表面积=上下两个底面+侧面积=底面积×2+底面周长×高。
【详解】(1)10×10×6=100×6=600(cm)
(2)(12×8+8×6+12×6)×2
=(96+48+72)×2
=(144+72)×2
=216×2
=432(cm)
(3)3.14×2×2×2+3.14×2×2×5
=6.28×2×2+6.28×2×5
=12.56×2+12.56×5
=25.12+62.8
=87.92(cm)
本题考查常见立体图形的表面积的计算,根据已给数据代入公式计算即可,注意不可遗漏面积单位。
30.9.72平方厘米,21.98平方米
【详解】试题分析:(1)阴影部分的面积=正方形的面积﹣半圆的面积,
(2)圆环的面积=大圆的面积﹣小圆的面积.
解:(1)4×4﹣3.14×(4÷2)2÷2,
=16﹣3.14×4÷2,
=16﹣6.28,
=9.72(平方厘米),
答:阴影部分的面积是9.72平方厘米.
(2)3.14×42﹣3.14×(4﹣1)2,
=3.14×16﹣3.14×9,
=50.24﹣28.26,
=21.98(平方米).
答:阴影部分的面积是21.98平方米.
点评:本题的关键是把不规则图形的面积,转化为规则图形面积相加或相减的方法进行计算.
31.(1)351.68cm2;(2)471cm2
【分析】(1)已知圆柱的底面直径和高,求圆柱的表面积,先求出圆柱的底面半径,用直径÷2=半径,然后用公式:S=πdh+2πr2 , 据此列式解答;
(2)已知圆柱的底面周长和高,求圆柱的表面积,先求出圆柱的底面半径,用底面周长÷2÷π=底面半径,然后用公式:S=Ch+2πr2 , 据此列式解答.
【详解】(1)圆柱的底面半径:8÷2=4(cm);
圆柱的表面积:
3.14×8×10+3.14×42×2
=25.12×10+3.14×16×2
=251.2+50.24×2
=251.2+100.48
=351.68(cm2)
(2)圆柱的底面半径:31.4÷2÷3.14=5(cm);
圆柱的表面积:
31.4×10+3.14×52×2
=314+3.14×25×2
=314+78.5×2
=314+157
=471(cm2)
32.251.2平方厘米;39.25平方厘米.
【详解】试题分析:(1)根据环形面积=外圆面积﹣内圆面积,把数据代入公式解答;
(2)通过旋转阴影部分是半径为5厘米的圆的,根据圆的面积公式:s=πr2,把数据代入公式解答.
解:(1)3.14×(122﹣82)
=3.14×(144﹣64)
=3.14×80
=251.2(平方厘米);
答:阴影部分的面积是251.2平方厘米.
(2)3.14×
=
=39.25(平方厘米);
答:阴影部分的面积是39.25平方厘米.
【点评】此题主要考查环形面积公式、圆的面积公式的灵活运用,关键是熟记公式.
33.27.87平方米
【分析】阴影部分的面积等于梯形的面积减去半圆的面积,根据梯形的面积公式:s=(a+b)×h÷2,圆的面积公式:s=πr2,把数据代入公式解答。
【详解】(6+8)×6÷2-3.14×(6÷2)2÷2
=14×6÷2-3.14×9÷2
=42-14.13
=27.87(平方米)
答:阴影部分的面积是27.87平方米。
34.答:阴影部分的面积是36平方厘米,周长30.84cm
【详解】试题分析:由图可知,阴影部分的周长是两个半径为6cm的圆的长度加上两条长为6cm的边;通过割补把阴影部分为半径6cm圆的面积补到空白处,则面积为边长6cm的正方形的面积;由此列式求得答案即可.
解:阴影部分的周长:
×2×3.14×6×2+6×2
=18.84+12
=30.84(cm)
阴影部分的面积:
6×6=36(cm2)
答:阴影部分的面积是36平方厘米,周长30.84cm.
点评:此题考查组合图形的周长和面积,注意根据图形的特点,适当进行割补.
35.1570平方厘米
【分析】观察图形可知,圆柱的底面半径是10厘米,高是15厘米,根据圆柱的表面积公式:S=2πr2+2πrh,用2×3.14×102+2×3.14×10×15即可求出圆柱的表面积。
【详解】2×3.14×102+2×3.14×10×15
=2×3.14×100+2×3.14×10×15
=628+942
=1570(平方厘米)
圆柱的表面积是1570平方厘米。
36.2.16平方米
【分析】根据公式:正方体的表面积=棱长×棱长×6,将数据代入公式计算即可。
【详解】0.6×0.6×6
=0.36×6
=2.16(m2)
37.50平方厘米
【详解】试题分析:根据题意和图形可知,大正方形的边长等于圆的直径,小正方形可以分成两个完全一样的三角形来计算它的面积,分成的三角形的底等于圆的直径,三角形的高等于圆的半径,根据正方形、三角形的面积公式计算出它们的面积,再求大、小正方形的面积之差,由此解答.
解:(5×2)×(5×2)﹣(5×2)×5÷2×2
=10×10﹣10×5÷2×2,
=100﹣50÷2×2,
=100﹣50,
=50(平方厘米);
答:大、小正方形的面积之差是50平方厘米.
点评:此题主要考查正方形、三角形的面积计算方法,根据正方形、三角形的面积公式解答即可.
38.0.125立方分米
【分析】根据正方体体积公式:正方体体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】0.5×0.5×0.5
=0.25×0.5
=0.125(立方分米)
39.周长:32.42厘米;面积:32.37平方厘米
【分析】阴影部分的周长等于一个直径为6厘米的圆周长的一半,加上梯形上底、下底、与长7.5厘米的腰长之和;阴影部分的面积用梯形的面积减去半圆的面积,据此解答即可。
【详解】周长:
(厘米)
面积:
(平方厘米)
40.7.74平方厘米
【详解】试题分析:我们运用正方形的面积减去圆的面积就是阴影部分的面积,运用圆的周长求出圆的直径,直径也是正方形的边长,由此即可解答.
解:正方形的边长(圆的直径):
18.84÷3.14=6(厘米);
阴影部分的面积:
6×6﹣3.14×(6÷2)2,
=36﹣28.26,
=7.74(平方厘米);
答:图中阴影部分的面积是7.74平方厘米.
点评:本题运用正方形的面积公式及圆的面积公式进行解答即可.
41.351.68dm3
【分析】该图形可以看作是一个圆柱和一个圆锥组合而成,求出两部分的体积再求和即可解答。
【详解】
(dm3)
42.50.24平方厘米
【分析】阴影部分的面积=半圆的面积-半圆内小圆的面积,根据圆的面积S=πr2,计算即可。
【详解】3.14×(16÷2)2÷2-3.14×(8÷2)2
=200.96÷2-50.24
=100.48-50.24
=50.24(平方厘米)
此题考查了有关圆的面积计算,找准数量关系,牢记圆的面积公式,认真计算即可。
43.表面积:232m2体积:160m3
表面积:216m2体积:189m3
【详解】表面积:(6×10+10×4)×2+4×2×2+(6-2)×2×2=232(m2)
体积:2×10×4+(6-2)×10×2=160(m3)
表面积:6×6×6=216(m2)
体积:6×6×6-3×3×3=189(m3)
44.10.8m3
【分析】将数据代入圆锥的体积公式:V=Sh,计算即可。
【详解】×9×3.6
=3×3.6
=10.8(m3)
45.10.8立方米;75.36立方分米;200.96立方厘米
【分析】直接用圆锥的体积:×底面积×高,代入数即可计算;
给出底面半径,运用圆锥的体积公式:3.14×半径×半径×高×,把数代入公式即可计算;
给出底面直径,先求出半径,之后再根据圆锥的体积公式:3.14×半径×半径×高×,把数代入公式即可计算;
【详解】×9×3.6
=3×3.6
=10.8(立方米);
3.14×3×3×8×
=28.26×8×
=226.08×
=75.36(平方分米);
8÷2=4(厘米)
3.14×4×4×12×
=50.24×12×
=602.88×
=200.96(立方厘米)
46.54平方分米
【详解】正方体表面积=棱长×棱长×6,根据公式计算表面积即可.
3×3×6=54(平方分米)
故答案为54平方分米.
47.100.48平方厘米
【分析】阴影部分的面积等于大圆的面积减去小圆的面积,公式:S=πr22-πr12=π(r22-r12)。
【详解】3.14×6×6-3.14×2×2
=3.14×(36-4)
=3.14×32
=100.48(平方厘米)
答:阴影部分的面积是100.48平方厘米。
48.25平方厘米
【分析】通过割补可知,阴影部分的面积相当于底为10厘米,高为(10÷2)厘米的三角形面积,根据三角形的面积=底×高÷2求出阴影部分的面积即可。
【详解】10÷2=5(厘米)
10×5÷2
=50÷2
=25(平方厘米)
阴影部分的面积是25平方厘米。
49.表面积: 2198cm2
体积: 7850cm3
【分析】底面积:立体图形的底所在面的面积;
侧面积:立体图形所有侧面面积的总和;
表面积:物体表面面积的总和叫做物体的表面积;
体积:物体所占空间的大小。
【详解】表面积:62.8×25+(62.8÷3.14÷2)2×3.14×2
=1570+100×3.14×2
=1570+628
=2198(cm2)
体积:(62.8÷3.14÷2)2×3.14×25
=100×3.14×25
=314×25
=7850(cm3)
小学阶段,关于长度、面积、体积的内容是相当多的,这是因为度量是几何学的核心。关于体积的度量,要让学生理解它度量的对象是三维空间的物体,除了善于利用公式,更重要的是帮助学生建立空间观念,使物体的长度、宽度、高度的表现在学生头脑里留下概括的印象。
50.401.92cm3
【分析】由图可知直径是8cm,那么半径是4cm,高是8cm,根据圆柱的体积公式:V=sh,把数据代入公式解答即可。
【详解】3.14×(8÷2)2×8
=3.14×42×8
=3.14×16×8
=50.24×8
=401.92(cm3)
答:圆柱体的体积是401.92cm3。
此题主要考查圆柱体积公式的灵活应用,关键是熟记公式。
51.628平方厘米
【分析】由图可知,平行四边形的底是圆的直径,平行四边形的高是圆的半径,根据平行四边形的面积表示圆的半径,代入圆的面积计算公式算出这个圆的面积。
【详解】解:设圆的半径为r。
2r×r=400
2r²=400
r²=400÷2
r²=200
圆的面积:200×3.14=628(平方厘米)
52.90平方厘米
【详解】试题分析:根据图意可知,对角线AC、BD将长方形平均分成了4个相等的三角形,阴影部分的面积占了其中的3份,所以阴影部分的面积就等于长方形面积的四分之三,列式解答即可得到答案.
解:15×8×,
=120×,
=90(平方厘米);
答:阴影部分的面积为90平方厘米.
点评:解答此题的关键是确定长方形中的两条对角线将长方形平均分成了四个相等的三角形.
53.长方体表面积:184cm2 体积:120cm3
正方体表面积:54cm2 体积:27cm3
54.37.68
【详解】解:3.14×(4+8)
=3.14×12
=37.68(厘米).
答:阴影部分的周长是37.68厘米.
【点评】此题主要考查半圆的周长的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.
55.100 cm3
【分析】观察可知,用图三水的体积-图二水的体积=两个小正方体的体积,再除以2就是一个小正方体体积。
【详解】(850-650)÷2
=200÷2
=100(cm3)
56.251.2cm2
【分析】根据圆柱的表面积公式:S=2πr2+πdh,据此代入数值进行计算即可。
【详解】2×3.14×(8÷2)2+3.14×8×6
=6.28×16+150.72
=100.48+150.72
=251.2(cm2)
57.376平方厘米
【详解】(10×6+10×8+6×8)×2=376(cm2)
答:长方体的表面积为376平方厘米.
58.6.88平方厘米
【分析】阴影部分的面积=长方形的面积-半径是4厘米的半圆的面积,据此列式解答。
【详解】4×8-3.14×42×
=32-25.12
=6.88(平方厘米)
59.10.26平方厘米
【详解】3.14× ÷2﹣[6×6÷2﹣ ×3.14×62],
=14.13﹣[18﹣14.13],
=14.13﹣3.87,
=10.26(平方厘米)
60.785立方厘米
【分析】将这个组合体看成一个圆柱和一个圆锥,用圆柱体积+圆锥体积即可。
【详解】10÷2=5(厘米)
3.14×5×8+3.14×5×6÷3
=628+157
=785(立方厘米)
本题考查了组合体的体积,圆柱体积=底面积×高,圆锥体积=底面积×高÷3。
61.19.74平方厘米
【分析】梯形的面积-半径为6厘米的圆的面积÷4即为阴影部分的面积。
【详解】
=48-28.26
=19.74(平方厘米)
62.49.68cm
【分析】通过观察图形可知,阴影部分的周长等于半径为12厘米的圆周长的加上直径为12厘米的圆周长的,再加上12厘米的线段;圆的周长公式C=2πr或C=πd,代入数据列式计算。
【详解】
=
(cm)
63.392.5dm3
【详解】3.14×(10÷2)2×15×=392.5dm3
64.31.4cm3;25.12cm3
【分析】圆柱体积=底面积×高,S=π;圆锥体积=×底面积×高,据此求解。
【详解】(1)r=d=×2=1(cm)
V=πr2h
=3.14×12×10
=31.4(cm3)
答:它的体积为31.4cm3。
(2)V=πr2h
=×3.14×22×6
=25.12(cm3)
答:它的体积为25.12cm3。
此题主要考查圆柱与圆锥的体积公式,熟记公式即可解答。
65.52平方厘米,24立方厘米;150平方分米,125立方分米
【详解】试题分析:根据“长方体的表面积=(长×宽+长×高+宽×高)×2”和“长方体的体积=长×宽×高”进行解答即可;
根据“正方体的表面积=棱长2×6”和“正方体的体积=棱长3”进行解答即可.
解:(1)长方体的表面积:
(4×3+4×2+3×2)×2,
=(12+8+6)×2,
=26×2,
=52(平方厘米),
体积:4×3×2=24(立方厘米);
(2)正方体的表面积:
5×5×6=150(平方分米),
体积:5×5×5=125(立方分米).
答:长方体的表面积是52平方厘米,体积是24立方厘米;正方体的表面积是150平方分米,体积是125立方分米.
点评:此题主要考查长方体、正方体的表面积和体积公式及其计算.
66.19.25cm2
【分析】阴影部分的面积=半圆的面积-三角形的面积,根据半圆面积公式:S=πr2,代入数据计算出结果后再减去三角形面积,据此解答。
【详解】52×3.14×-20
=25×3.14×-20
=78.56×-20
=39.25-20
=19.25(cm2)
67.
【分析】阴影部分的面积=梯形的面积-直角扇形的面积,直角扇形的面积是圆面积的。
【详解】
=10×4÷2-3.14×4
=20-12.56
=7.44(cm2)
本题考查求组合图形中的阴影部分的面积,明确阴影部分与各图形之间的关系是关键。
68.表面积为:49600平方厘米;体积为:640000立方厘米
【分析】图中组合图形的表面积等于长为100厘米,宽为80厘米,高为(60+50)厘米的长方体的表面积减去4个长为50厘米,宽为(100-40)÷2厘米的长方形的面积,分别利用长方体的表面积和长方形的面积公式,再相减即可求出组合图形的表面积;
图中的组合图形的体积等于长为100厘米,宽为80厘米,高为(60+50)厘米的长方体的体积减去2个长为(100-40)÷2厘米,宽为80厘米,高为50厘米的长方体的体积,利用长方体的体积公式,再相减即可求出组合图形的体积。
【详解】(100-40)÷2
=60÷2
=30(厘米)
100×80×2+100×(60+50)×2+80×(60+50)×2-4×50×30
=16000+100×110×2+80×110×2-6000
=16000+22000+17600-6000
=49600(平方厘米)
100×80×(60+50)-2×30×80×50
=100×80×110-4800×50
=880000-240000
=640000(立方厘米)
即图形的表面积是49600平方厘米,体积是640000立方厘米。
69.39.25cm2,25.12 cm2
【分析】(1)根据图意可知,阴影部分面积=大半圆面积-两个不同的小半圆面积,再根据圆面积公式求解;
(2)因为三角形内角和是180°,阴影部分的面积和是半径为4厘米的半圆面积,根据图意可知,阴影部分面积=三角形面积-半圆面积,据此解答。
【详解】(1)3.14×[(10+5)÷2]²÷2-3.14×(10÷2)²÷2-3.14×(5÷2)²÷2
=3.14×56.25÷2-3.14×25÷2-3.14×6.25÷2
=88.3125-39.25-9.8125
=39.25(平方厘米)
(2)3.14×4²÷2
=50.24÷2
=25.12(平方厘米)
70.30.87平方厘米
【分析】观察图形可知,阴影部分的面积=梯形的面积-半圆的面积,梯形的上底相当于圆的直径,然后根据梯形的面积=(上底+下底)×高÷2,圆的面积公式:S=πr2,据此代入数值进行计算即可。
【详解】(6+12)×5÷2-3.14×(6÷2)2÷2
=18×5÷2-3.14×9÷2
=45-14.13
=30.87(平方厘米)
71.314平方厘米;785立方厘米
【分析】根据圆柱的侧面积公式:S=和圆柱的体积公式:V=,已知圆柱的半径为5厘米,高为10厘米,代入到公式中,分别求出圆柱体的侧面积和体积。
【详解】2×3.14×5×10
=6.28×5×10
=314(平方厘米)
3.14×52×10
=3.14×25×10
=785(立方厘米)
72.1.72
【分析】根据图形可知,要求阴影部分的面积,应该用长方形的面积减去半圆的面积即可。
【详解】4×2−3.14×(4÷2)2÷2
=8−6.28
=1.72
本题考查长方形和圆的面积公式,明确圆的直径相当于长方形的长是解题的关键。
73.1.14平方厘米
【详解】3.14×(2÷2)×(2÷2)-2×2÷2=1.14(平方厘米)
74.565.2cm3
【分析】题目中的圆锥体结合图能清楚的看到圆锥的底面和高,直接利用圆锥的体积公式V圆锥=×Sh计算即可。
【详解】3.14×62×15×
=3.14×36×15×
=113.04×15×
=1695.6×
=565.2(cm3)
学生在课上经过合情推理的环节,在实践中,结合思辨与猜想,体会到圆锥体积公式的由来。掌握其计算方法,也就能解决简单的实际问题。
75.392.5立方厘米;25.12立方厘米
【分析】根据圆柱体积=底面积×高,圆锥体积=底面积×高÷3,列式计算即可。
【详解】3.14×(10÷2)²×5
=3.14×25×5
=392.5(立方厘米)
3.14×2²×6÷3=25.12(立方厘米)
76.24cm
77.388.4米
【分析】运用圆的周长计算公式是C=πd进行计算,加上2个100米即可。
【详解】3.14×60+100×2
=188.4+200
=388.4(米)
图形的周长是388.4米。
78.75.36平方厘米
【分析】根据圆柱的表面积公式计算即可。
【详解】3.14×2×2+3.14×2×2×4
=25.12+50.24
=75.36(平方厘米)
本题考查了圆柱的表面积,圆柱表面积=底面积×2+侧面积。
79.18.84平方厘米
【分析】根据图意可知,根据圆环面积=大圆面积-小圆面积,阴影部分(半圆环)面积=圆环面积÷2,代入数据求解。
【详解】π[(4-2)+2]²-π(4÷2)²
=16π-4π
=12π
=37.68(平方厘米)
37.68÷2=18.84(平方厘米)
80.32.5平方厘米
【分析】根据图所示,可把组合图形分成一个直角梯形和一个圆,阴影部分的面积等于梯形的面积减去圆的面积再加上圆的面积减去三角形面积的差,列式解答即可得到答案。
【详解】[(5+8+5)×5÷2-×3.14×52]+(×3.14×52-5×5÷2),
=[18×5÷2-0.785×25]+(0.785×25-25÷2),
=[90÷2-19.625]+(19.625-12.5),
=[45-19.625]+7.125,
=25.375+7.125,
=32.5(平方厘米);
答:阴影部分的面积为32.5平方厘米.
此题主要考查的是梯形的面积公式(上底+下底)×高÷2、三角形的面积公式底×高÷2和圆的面积公式S=πr2的应用。
81.表面积是126平方厘米,体积是90立方厘米;
表面积是96平方厘米,体积是64立方厘米
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。将数据代入公式,求出题中长方体和正方体的表面积和体积即可。
【详解】(6×3+6×5+3×5)×2
=(18+30+15)×2
=63×2
=126(平方厘米)
6×3×5=90(立方厘米)
所以,这个长方体的表面积是126平方厘米,体积是90立方厘米。
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)
所以,这个正方体的表面积是96平方厘米,体积是64立方厘米。
82.31.4厘米
【分析】已知圆的半径是5厘米,根据即可求出圆的周长。
【详解】2×3.14×5
=6.28×5
=31.4(厘米)
所以,圆的周长是31.4厘米。
83.10.26平方厘米
【详解】试题分析:观察图形可知,阴影部分的面积等于图中半圆的面积减去空白处1的面积,由此利用半圆的面积公式求出半圆的面积是:3.14×÷2=14.13平方厘米,只要再求出空白处1的面积即可解答;因为三角形ABC是等腰直角三角形,所以∠A=45度,则空白处1的面积=三角形ABC的面积﹣圆心角是45度,半径是6厘米的扇形的面积,由此利用三角形和扇形的面积公式即可解答.
解:3.14×÷2﹣[6×6÷2﹣×3.14×62],
=14.13﹣[18﹣14.13],
=14.13﹣3.87,
=10.26(平方厘米);
答:阴影部分的面积是10.26平方厘米.
点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,将阴影部分重组,从而利用已知条件求得阴影部分的面积.
84.面积9cm2;周长15.42cm
【分析】
如图,把右面阴影圆补到左边空白部分,这样阴影部分组成一个边长为3cm的正方形;根据正方形的面积=边长×边长,即可求出阴影部分的面积。
阴影部分的周长=圆周长的一半+2个3cm的线段,根据圆的周长公式C=2πr,代入数据计算即可求解。
【详解】阴影部分的面积:
3×3=9(cm2)
阴影部分的周长:
2×3.14×3÷2+3×2
=9.42+6
=15.42(cm)
阴影部分的面积是9cm2,阴影部分的周长是15.42cm。
85.体积:125立方分米
表面积:220平方厘米
【分析】根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,据此代入数值进行计算即可。
【详解】体积:5×5×5
=25×5
=125(立方分米)
表面积:(10×5+10×4+5×4)×2
=(50+40+20)×2
=110×2
=220(平方厘米)
86.125.6cm2;87.92dm3
【分析】圆柱的表面积=侧面积+底面积×2,圆柱的体积:,圆锥的体积公式:,代入数据解答即可。
【详解】12.56÷3.14=4(cm)
3.14×4×8+3.14×(4÷2)2×2
=12.56×8+3.14×4×2
=100.48+12.56×2
=100.48+25.12
=125.6(cm2)
4÷2=2(dm)
3.14×22×6+×3.14×22×3
=3.14×4×6+×3.14×4×3
=12.56×6+×12.56×3
=75.36+×37.68
=75.36+12.56
=87.92(dm3)
87.9.85m;3.925m2
【分析】由图可知,阴影部分的周长=小圆周长×+大圆周长×+环宽×2,利用“”表示大圆和小圆的周长,最后求出阴影部分的周长;
阴影部分的面积等于整个环形面积的,利用“”求出阴影部分的面积,据此解答。
【详解】周长:2×3.14×(2+1)×+2×3.14×2×+1×2
=2×3.14×3×+2×3.14×2×+1×2
=(2×)×(3.14×3)+(2×2×)×3.14+2
=×9.42+3.14+2
=4.71+3.14+2
=9.85(m)
面积:3.14×[(2+1)2-22]×
=3.14×[32-22]×
=3.14×5×
=15.7×
=3.925(m2)
所以,阴影部分的周长是9.85m,面积是3.925m2。
88.23.55 cm 21.195 cm2
【详解】思路分析:根据圆的面积=π×r×r和长方形的面积=长×宽,长方形的宽与r相等,可得:长方形的长=π×r=3.14×3=9.42厘米,则(1)阴影部分的周长为:长方形的周长-2r+×圆的周长;(2)阴影部分的面积为:长方形的面积-圆的面积,由此即可解答问题.
名师详解:解:长方形的长是:
3.14×3=9.42(厘米);
则阴影部分的周长是:
(9.42+3)×2-3×2+3.14×3×2×,
=24.84-6+4.71,
=23.55(厘米);
阴影部分的面积是:
9.42×3-×3.14×32,
=28.26-7.065,
=21.195(平方厘米);
答:阴影部分的周长是23.55厘米,面积是21.195平方厘米.
易错提示:注意的是,利用圆与长方形的面积相等,求出长方形的长是解答此题的关键,由此再根据相应的公式解决问题.建议这是一个较难的题,课下可以多练习几道这样的题目.
89.10.84平方厘米
【分析】由图意可知:阴影部分的面积=大半圆的面积﹣空白三角形的面积﹣小半圆的面积,又因小半圆的直径等于大半圆的半径,空白三角形的两条直角边都等于大半圆的半径,于是利用三角形和圆的面积公式即可求解.
【详解】3.14×42÷2﹣4×4÷2﹣3.14×(4÷2)2÷2,
=25.12﹣8﹣6.28,
=10.84(平方厘米);
答:阴影部分的面积是10.84平方厘米.
90.87.92平方米
【分析】圆柱的侧面积=底面周长×高,圆柱的表面积=圆的侧面积+两个底面积,据此解答即可。
【详解】侧面积:3.14×2×2×5
=12.56×5
=62.8(平方米)
表面积:62.8+3.14×22×2
=62.8+25.12
=87.92(平方米)
91.阴影部分周长为18.84厘米;阴影部分的面积为2.28平方厘米
【详解】试题分析:(1)阴影部分的周长可看作由下面几部分组成:大圆周长的一半、中间小圆的周长、下面两个小半圆周长的一半,并且小圆直径和两个小半圆直径都相等,根据圆的周长公式解答即可;
(2)求阴影部分的面积可作几条辅助线,如图:将阴影1、2、3、4分别移到空白1、2、3、4,处,那么用大半圆的面积减去大三角形的面积即阴影部分的面积,据此解答.
解:(1)阴影部分周长:3.14×4÷2+3.14×(4÷2)×2
=6.28+12.56
=18.84(厘米)
(2)阴影部分的面积:3.14×(4÷2)2÷2﹣4×(4÷2)÷2
=6.28﹣4
=2.28(平方厘米)
92.14.25平方厘米;18.87平方厘米
【分析】图一阴影部分的面积=半圆的面积-三角形的面积;
图二阴影部分的面积=梯形的面积-半圆的面积
【详解】3.14×(10÷2)²÷2-10×(10÷2)÷2
=39.25-25
=14.25(平方厘米);
(3+8)×6÷2-3.14×(6÷2)²÷2
=33-14.13
=18.87(平方厘米)
93.464平方分米
【分析】圆柱体沿着直径和高对半锯开,截面是一个以圆柱的底面直径和高为边长的长方形,所以这半圆柱的表面积就是圆柱的表面积的一半加上截面的面积,由此利用圆柱的表面积和长方形的面积公式即可解答。
【详解】[3.14×(10÷2)2×2+3.14×10×15]÷2+10×15
=[3.14×52×2+31.4×15]÷2+150
=[3.14×25×2+31.4×15]÷2+150
=[78.5×2+471]÷2+150
=[157+471]÷2+150
=628÷2+150
=314+150
=464(平方分米)
它的表面积是464平方分米。
94.表面积:150平方厘米 392平方厘米;体积:125立方厘米 480立方厘米
95.表面积:117.68dm2;体积:89.12dm3
【分析】观察图形可知,该图形的表面积等于正方体五个面的面积加上直径为4dm的圆的面积,再加上底面直径和高都为4dm的圆柱的侧面积的一半,再根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,据此进行计算即可;该图形的体积等于正方体的体积加上圆柱的体积的一半,根据正方体的体积公式:V=a3,圆柱的体积公式:V=πr2h,据此进行计算即可。
【详解】表面积:
4×4×5+3.14×(4÷2)2+×3.14×4×4
=16×5+3.14×4+25.12
=80+12.56+25.12
=92.56+25.12
=117.68(dm2)
体积:
4×4×4+×3.14×(4÷2)2×4
=16×4+×3.14×4×4
=64+25.12
=89.12(dm3)
96.580m2;800m3
【分析】根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,列式计算即可。
【详解】表面积:(16×10+16×5+5×10)×2
=(160+80+50)×2
=290×2
=580(m2)
体积:16×10×5=800(m3)
97.(1)6.25;(2)6.88
【分析】(1)阴影部分的面积是底为5cm,高为(5÷2)cm的三角形,根据三角形的面积=底×高÷2,代入数据即可解答。
(2)先求出宽4cm,长(4×2)cm的长方形面积和直径为4cm的两个圆的面积,再用长方形的面积减去两个圆的面积,即是阴影部分的面积。
【详解】(1)5×(5÷2)÷2
=5×2.5÷2
=12.5÷2
=6.25(cm2)
(2)4×(4×2)
=4×8
=32(cm2)
(4÷2)2×3.14×2
=4×3.14×2
=12.56×2
=25.12(cm2)
32-25.12=6.88(cm2)
98.33.48平方厘米
【分析】依题意可知,梯形的面积-半圆面积=阴影部分面积,据此解答。
【详解】(6×2+18)×6÷2-6²÷2
=90-56.52
=33.48(平方厘米)
阴影部分的面积是33.48平方厘米。
99.35.4厘米
【分析】已知内圆的直径是8cm,外圆的直径是12cm,根据圆的周长公式C=πd,分别求出内圆和外圆的周长,然后分别求出它们周长的一半,把它们周长的一半相加再加上12-8即可解答。
【详解】3.14×8÷2+3.14×12÷2+(12-8)
=12.56+18.84+4
=31.4+4
=35.4(厘米)
100.769.3立方厘米;527.52平方厘米
【详解】体积:3.14(14÷2)25
=3.14495
=769.3(立方厘米)
表面积:3.14(14÷2)22+3.14145
=307.72+219.8
=527.52(平方厘米)
(浙江期末真题精选)06-图形计算100题(提高)2023年五年级下册数学高频易错题(人教版): 这是一份(浙江期末真题精选)06-图形计算100题(提高)2023年五年级下册数学高频易错题(人教版),共52页。试卷主要包含了图形计算等内容,欢迎下载使用。
(浙江期末真题精选)07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版): 这是一份(浙江期末真题精选)07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版),共44页。试卷主要包含了图形计算等内容,欢迎下载使用。
(浙江期末真题精选)11-综合计算100题(提高)2023年六年级下册数学高频易错题(人教版): 这是一份(浙江期末真题精选)11-综合计算100题(提高)2023年六年级下册数学高频易错题(人教版),共62页。试卷主要包含了口算,竖式计算,脱式计算,解方程或比例,化简比和求比值,看图列式,图形计算等内容,欢迎下载使用。













