第一单元《圆柱和圆锥》（原卷版+解析版）——【期末复习】2022-2023学年六年级下册数学单元复习知识点+练习学案（北师大版）

这是一份第一单元《圆柱和圆锥》（原卷版+解析版）——【期末复习】2022-2023学年六年级下册数学单元复习知识点+练习学案（北师大版），文件包含第一单元《圆柱和圆锥》解析版期末复习2022-2023学年六年级下册数学单元复习知识点+练习学案北师大版docx、第一单元《圆柱和圆锥》原卷版期末复习2022-2023学年六年级下册数学单元复习知识点+练习学案北师大版docx等2份学案配套教学资源，其中学案共58页， 欢迎下载使用。
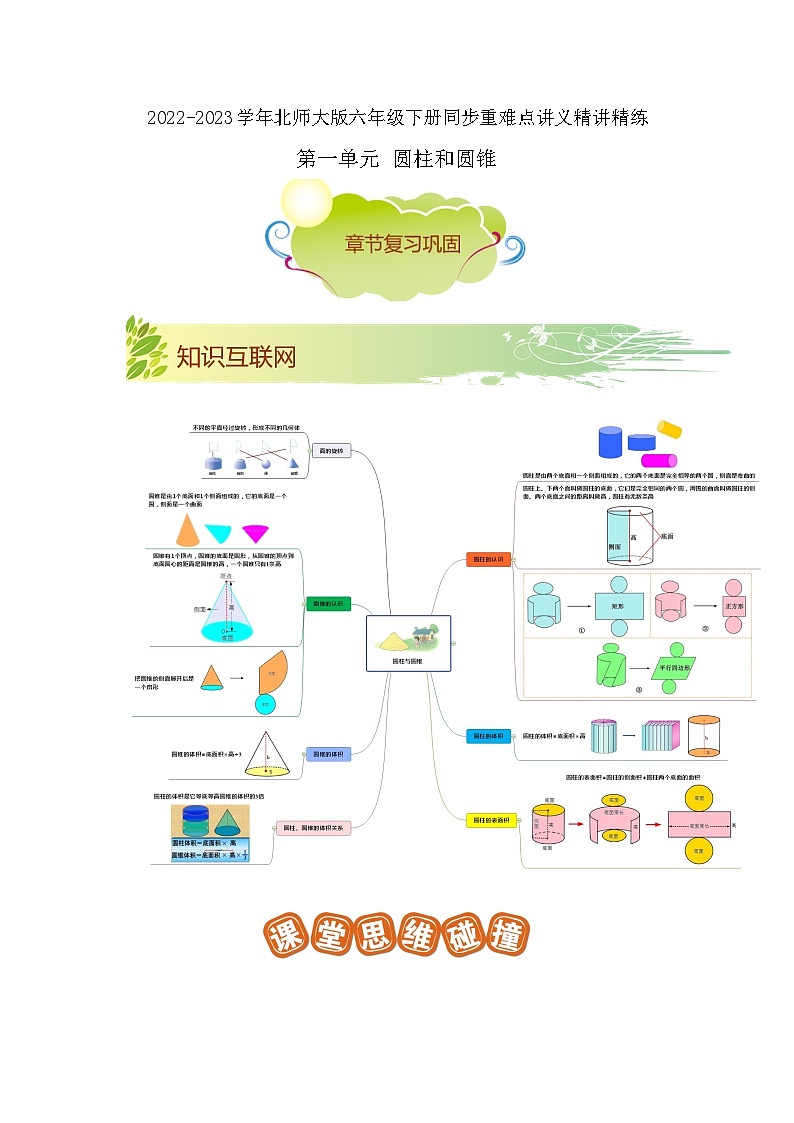
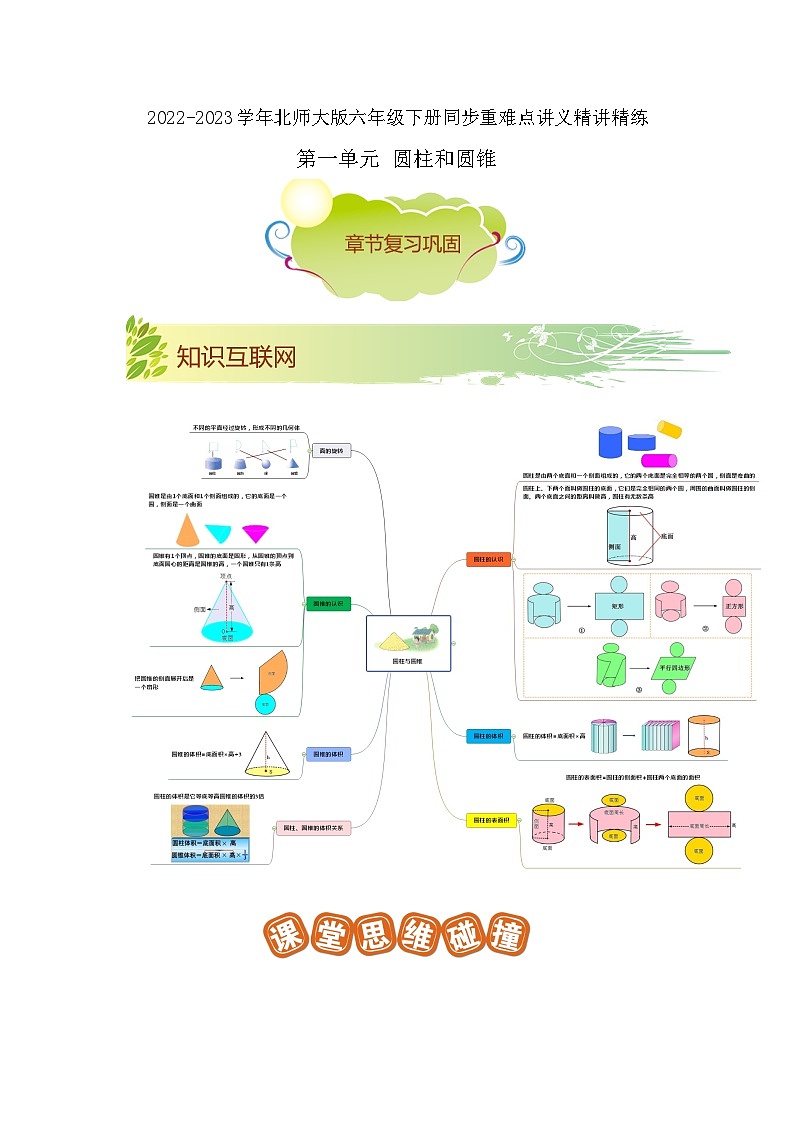
2022-2023学年北师大版六年级下册同步重难点讲义精讲精练
第一单元 圆柱和圆锥






知识点一：面的旋转、圆柱和圆锥的特征
1. 点的运动形成线，线的运动形成面，面的运动形成体，这就是“点、线、面、体”之间的关系，这个关系可以简记为“点动成线，线动成面，面动成体”。
2.圆柱是由2个大小相同的圆面和1个曲面围成的，圆柱上下粗细均匀。圆锥是由1个圆面和1个曲面围成的。
3.圆柱的特征：（1）圆柱有两个底面和一个侧面；（2）两个底面是完全相同的圆，侧面是一个曲面；（3）圆柱有无数条高，所有的高都相等。
圆锥的特征：（1）圆锥有一个底面和一个侧面；（1）圆锥的底面是一个圆，侧面是一个曲面；（3）圆锥只有一条高。
4. 圆柱和圆锥的切面：
（1）把圆柱平行于底面横切，切面是大小相同的圆；沿底面直径纵切，切面是大小相同的长方形。（2）把圆锥横切，每个切面是圆，但大小不同；沿底面直径纵切，切面是大小相同的等腰三角形。
知识点二：圆柱的表面积
1.如果用S表表示圆柱的表面积，S侧 表示圆柱的侧面积，S底 表示圆柱的底面积，d表示底面的直径，r表示底面的半径，h表示圆柱的高，那么圆柱的表面积的计算公式可以表示为
S表=S侧+2S底 或S表=πdh+2π（d÷2）2或S表=2πrh+2πr2
2. 在解决实际问题时，并不是所有的圆柱形物体都有两个底面，有的只有一个底面，有的没有底面，解题时要根据实际情况选择合适的解题方法。
3. 用同一张长方形纸片可以围成底面积不同的两个圆柱。用宽作为圆柱的底面周长，所围成的圆柱的底面积小；用长作为圆柱的底面周长，所围成的圆柱的底面积大。
4. 横截圆柱后求表面积时，侧面积不变，底面积会发生变化，变化的规律是每截一次增加两个底面，截的次数比截成的段数少1。
知识点三：圆柱的体积
1. 圆柱的体积=底面积×高，用字母表示是V=Sh。
2. 计算一个圆柱的体积时，如果已知这个圆柱的高和底面半径或底面直径或底面周长，要先求出底面积，再求体积，也可以列综合算式计算。
（1）已知圆柱的底面积S和高h，求圆柱体积的计算方法：V=Sh。
（2）已知圆柱的底面半径r和高h，求圆柱体积的计算方法：V=πr2h
（3）已知圆柱的底面直径d和高h，求圆柱体积的计算方法：V=π（d÷2）2h
（4）已知圆柱的底面周长C和高h，求圆柱体积的计算方法：V=π（C÷π÷2）2h
3. 物体完全浸没在水中，物体的体积等于升高的那部分水的体积。
应用等量代换法可以将不规则物体的体积计算转化为圆柱的体积计算。
利用体积不变的特性，应用转化的思想方法，把不规则的图形转化为规则的图形来计算，能帮助我们解决许多生活中的复杂问题。
知识点四：圆锥的体积
1.圆锥的体积是与它等底等高的圆柱体积的。。
2.圆锥体积的计算方法：
（1）已知底面半径r和高h，求圆锥体积的方法：V=13πr2h；
（2）已知底面直径d和高h，求圆锥体积的方法：V=13π（d÷2）2h；
（3）已知底面周长C和高h，求圆锥体积的方法：V=13π（C÷x÷2）2h
3. 圆柱和圆锥的体积与高分别相等，则它们的底面积之间的关系是Sm推=3Sm壮；圆柱和圆锥的体积与底面积分别相等，则它们的高之间的关系是h锥=3h柱

考点1：圆柱的特征
【典例分析01】（2022春•梁山县期末）硬币的上下两个面是（　　）
A．长方形 B．正方形 C．圆形
【思路点拨】硬币是一个圆柱，圆柱就是由两个大小相同的圆和一个侧面组成的，它的底面是完全相同的两个圆，据此解答。
【规范解答】解：硬币的上下两个面是大小相等的圆形。
故选：C。
【考点评析】本题考查了圆柱的特征。
【典例分析02】（2022•曹县）如图中圆柱的底面周长是25.12cm，高是15dm，现用包装绳包扎，至少需要多长的包装绳？（接头处需15cm）

【思路点拨】根据题意和图形可知，所需彩带的长度等于4条高，4条直径，再加打结处用的15厘米，由此列式解答。
【规范解答】解：15分米＝150厘米
底面直径：
25.12÷3.14＝8（厘米）
8×4+150×4+15
＝32+600+15
＝647（厘米）
答：至少需要647厘米的包装绳。
【考点评析】此题属于圆柱体知识的实际应用，解答关键是弄清是如何捆扎的，也就是弄清是求哪些数据的长度和。
【随堂演练01】（2021秋•沈阳期末）从上面看，看到的形状是（　　）
A． B． C．
【思路点拨】根据题意，从上面看，看到的形状是，据此解答即可。
【规范解答】解：从上面看，看到的形状是。
故选：C。
【考点评析】本题考查了从不同方向观察物体的知识，结合图示解答即可。
【随堂演练02】（2021春•蓟州区月考）用塑料绳捆扎一个圆柱形的蛋糕盒（如图），打结处正好是底面圆心，打
结用去绳长15厘米．扎这个盒子至少用去塑料绳多少厘米？

【思路点拨】观察图形，发现用去塑料绳子的长度就是4个高和4个直径的长度和再加上15厘米．
【规范解答】解：40×4+20×4+15
＝160+80+15
＝255（厘米）
答：扎这个盒子至少用去塑料绳255厘米．
【考点评析】考查了对圆柱特征的认识，不要忘了加上15厘米．
考点2：圆锥的特征
【典例分析03】（2020•农安县）标出下面圆锥的顶点、高、底面半径．

【思路点拨】根据圆锥的特征，圆锥的底面是一个圆，侧面是一个曲面，从顶点到底面圆心的距离叫做圆锥的高。据此解答。
【规范解答】解：

【考点评析】此题考查的目的是理解掌握圆锥的特征、以及圆锥各部分的名称。
【典例分析04】．（2021•农安县模拟）如图各图形中，是圆柱的在括号里画“〇”，是圆锥的在括号里画“△”．

【思路点拨】根据圆柱、圆锥的特征，圆柱的上、下底面是完全相同的两个圆，侧面是曲面，侧面沿高展开是一个长方形．圆锥的底面是一个圆，侧面是曲面，侧面展开是一个扇形．据此解答即可．
【规范解答】解：

【考点评析】此题考查的目的是理解掌握圆柱、圆锥的特征及应用．
【随堂演练03】（2022•济南）如图是一个直角三角形，如果以a边为轴旋转一周，将形成一个 　圆锥　，这个立体图形的高是 　a　，b是它的 　底面半径　，它的底面周长是 　6.28b　。

【思路点拨】以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。无论旋转到什么位置，不垂直于轴的边都叫做圆锥的母线。圆锥的高：圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。
【规范解答】解：下面是一个直角三角形，如果以a边为轴旋转一周，将形成一个圆锥，这个立体图形的高是a，b是它的底面半径，它的底面周长是：
3.14×b×2＝6.28b。

故答案为：圆锥；a；底面半径；6.28b。
【考点评析】本题考查了圆锥的特征，要有一定的空间想象能力。
【随堂演练04】（2021春•宁阳县期末）在正方形铁皮上剪下一个圆和一个扇形，恰好围成一个圆锥模型（如图）。如果扇形的半径为8厘米，那么，做这个圆锥模型至少需要多少平方厘米的铁皮？（写出主要过程）

【思路点拨】首先设圆的半径为r，求出半径为r的圆的面积，然后用扇形的面积加上圆的面积即可求得圆锥的表面积。
【规范解答】解：设圆的半径为r，
因为扇形的弧长等于圆锥底面周长，
所以2π×8÷4＝2πr
r＝2
圆锥的表面积：S扇形+S圆＝π×82÷4+π×22
＝16π+4π
＝20π
＝62.8（平方厘米）
答：做这个圆锥模型至少需要62.8平方厘米的铁皮。
【考点评析】本题考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长；本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解。
考点3：圆柱的展开图
【典例分析05】（2022春•固始县期中）一个圆柱的侧面展开图是一个正方形，这个圆柱的高是25.12cm，那么圆柱的底面周长是 　25.12　cm，底面直径是 　8　cm。
【思路点拨】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形或正方形，这个长方形的长等于圆柱的底面周长，宽等于圆柱的高，根据圆的周长公式：C＝2πr，那么d＝C÷π，把数据代入公式解答。
【规范解答】解：25.12÷3.14＝8（厘米）
答：圆柱的底面周长是25.12厘米，底面直径是8厘米。
故答案为：25.12、8。
【考点评析】此题考查的目的是理解掌握圆柱侧面展开图的特征，以及圆的周长公式的灵活运用，关键是熟记公式。
【典例分析06】（2022春•宁阳县期末）如图有一张长方形铁皮。剪下两个圆及一长方形B，正好可以做成一个圆柱体。这个圆柱体的底面半径为3分米。则长方形B的长是 　18.84　分米，宽是 　6　分米。

【思路点拨】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形，这个长方形的长等于圆柱的底面周长，宽等于圆柱的高。据此解答即可。
【规范解答】解：长方形B的长：
3.14×3×2＝18.84（分米）
宽：3×2＝6（分米）
答：长方形B的长是18.84分米，宽是 6分米。
故答案为：18.84；6。
【考点评析】此题考查的对面是理解掌握圆柱展开图的特征，结合题意分析解答即可。
【随堂演练05】（2022•永春县）有以下四种型号的纸皮，小豪想自己制作一个漂亮的笔筒。你认为它应该选择 　a　和 　d　，才能制作成功呢？请说明理由。

【思路点拨】圆柱的侧面沿高剪开的展开图是一个长方形（或正方形），这个长方形（或正方形）的长等于圆柱底面的周长，宽等于圆柱的高，据此利用πr2求出底面周长与长方形的长作比较即可。
【规范解答】解：3.14×3×2
＝3.14×6
＝18.84
3.14×4×2
＝3.14×8
＝25.12
由此可知因为半径为4的底面周长是25.12与长方形的长相等，符合圆柱的侧面展开图的样子。
故答案为：a，d。
【考点评析】此题主要考查了圆柱与圆柱的侧面展开图之间的关系，再根据相应的公式与基本的数量关系解决问题。
【随堂演练06】（2022•吉首市）下面哪个图形是圆柱的展开图形（单位：cm）（　　）
A． B．C．
【思路点拨】根据圆柱的侧面沿高剪开的展开图是一个长方形（或正方形），这个长方形（或正方形）的长等于圆柱底面的周长，宽等于圆柱的高即可解答。
【规范解答】解：图形是圆柱的展开图形。
故选：A。
【考点评析】本题主要考查圆柱的侧面沿高剪开的展开图是一个长方形（或正方形），这个长方形（或正方形）的长等于圆柱底面的周长，宽等于圆柱的高。
考点4：圆柱的侧面积和表面积
【典例分析07】（2022•天津模拟）求如图形的表面积。（单位：厘米）

【思路点拨】利用圆环的面积公式：S＝π（R2﹣r2），再乘2，即可求出这个图形左右两边圆环的面积，里面小圆柱的侧面积可通过公式：S＝πdh求出，外面大圆柱的侧面积同样可通过公式：S＝πdh求出，注意两个圆柱的直径不同，把2个圆环的面积加上大小圆柱的侧面积即是这个图形的表面积。
【规范解答】解：圆环面积：R＝6÷2＝3（厘米），r＝4÷2＝2（厘米）
（3×3﹣2×2）×3.14×2
＝（9﹣4）×3.14×2
＝5×3.14×2
＝31.4（平方厘米）
外侧面积：6×3.14×8＝150.72（平方厘米）
内侧面积：4×3.14×8＝100.48（平方厘米）
表面积：31.4+150.72+100.48＝282.6（平方厘米）
答：图形的表面积是282.6平方厘米。
【考点评析】本题考查了圆柱的侧面积公式及圆环面积的公式的应用。
【典例分析08】（2022•神木市）一个圆柱的底面周长是18.84米，高是2米，则这个圆柱的表面积是（　　）平方米。
A．94.2 B．65.94 C．56.52 D．37.68
【思路点拨】先由底面周长是18.84米求得圆柱的底面半径，再利用S＝Ch+2πr2求得它的表面积是多少即可。
【规范解答】解：18.84÷3.14÷2＝3（米）
18.84×2+3.14×32×2
＝37.68+3.14×18
＝37.68+56.52，
＝94.2（平方米）
答：它的表面积是94.2平方米。
故选：A。
【考点评析】此题是考查圆柱表面积的计算，可利用其表面积公式公式来解答。
【随堂演练07】（2022•金水区）把一个高是10厘米的圆柱如图所示切开、拼成一个近似于长方体的立体图形，表面积增加了40平方厘米。这个圆柱的侧面积是（　　）平方厘米。

A．40 B．12.56 C．125.6
【思路点拨】根据圆柱体积公式的推导过程可知，把一个圆柱切拼成一个近似长方体，拼成的长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积，每个切面的长等于圆柱的高，每个切面的宽等于圆柱的底面半径，据此可以求出圆柱的底面半径，然后根据圆柱的侧面积公式：S＝2πrh，把数据代入公式解答。
【规范解答】解：40÷2÷10
＝20÷10
＝2（厘米）
2×3.14×2×10
＝12.56×10
＝125.6（平方厘米）
答：这个圆柱的侧面积是125.6平方厘米。
故选：C。
【考点评析】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用，圆柱侧面积公式的灵活运用，关键是熟记公式。
【随堂演练08】（2021秋•吴堡县期末）计算下面图形的表面积。

【思路点拨】由于上面的圆柱与下面的长方体粘合在一起，所以上面的圆柱只求侧面积，下面长方体求表面积，然后相加起来即可，根据圆柱的侧面积公式：S＝πdh，长方体的表面公式：S＝（ab+ah+bh）×2，把数据代入公式解答。
【规范解答】解：3.14×4×6+（10×4+10×5+4×5）×2
＝12.56×6+（40+50+20）×2
＝75.36+110×2
＝75.36+220
＝295.36（平方分米）
答：它的表面积是295.36平方分米。
【考点评析】此题主要考查圆柱的表面积公式、长方体的表面积公式的灵活运用，关键是熟记公式。
考点5：圆柱的体积
【典例分析09】计算下面各圆柱体的体积。（单位：cm）

【思路点拨】圆柱的体积等于底面积乘高，还可以利用体积公式V＝πr2h计算，据此代入数字计算即可。
【规范解答】解：60×4＝240（立方厘米）
3.14×12×5
＝3.14×5
＝15.7（立方厘米）
3.14×（6÷2）2×10
＝3.14×9×10
＝3.14×90
＝282.6（立方厘米）
【考点评析】本题考查了圆柱体积公式的应用。
【典例分析10】（2022•满洲里市）求瓶子的体积（单位：cm）

【思路点拨】根据体积的意义可知，瓶子无论正放还是倒放，瓶子里水的体积不变，通过关系图形可知，正放时，水的高是4厘米，倒放时，水的高是5厘米，这个瓶子的体积相当于底面积为10平方厘米，高是（7+4﹣5+4）厘米的圆柱的容积。根据圆柱的容积公式：V＝Sh，把数据代入公式解答。
【规范解答】解：10×（7+4﹣5+4）
＝10×（11﹣5+4）
＝10×（6+4）
＝10×10
＝100（立方厘米）
答：瓶子的体积是100立方厘米。
【考点评析】此题主要考查圆柱的容积（体积）公式的灵活运用，关键是熟记公式。
【随堂演练09】（2022•金湾区）图中运用了“转化”思想方法的有（　　）

A．①和② B．②和③ C．①和③ D．①②③
【思路点拨】根据圆周长的探索过程，小数乘法的计算方法，以及瓶子容积的推导过程进行解答。
【规范解答】解：探索圆的周长时：这是把曲线的长度转化成了直线的长度，运用了“转化”的思想；
计算小数乘法时，首先把小数“转化”为整数，按照整数乘法的计算再计算出积，再看两个因为共有几位小数，就从积的右边起数出几位点上小数点。此过程运用“转化”的方法。
应用颠倒瓶子的方法求瓶子的体积，这里运用了转化的数学思想方法。
故选：D。
【考点评析】转化思想就是将未知解法或难以解决的问题，通过观察、分析、联想、类比等思维过程，选择恰当的方法进行变换，化归为已知知识范围内已经解决或容易解决的问题方法的数学思想；是小学阶段常用的一种数学思想。
【随堂演练10】（2022•宝安区）（如图）在圆柱体水桶中装满水后倒入一个无盖的长方体玻璃鱼缸中，正好将鱼缸装满。已知圆柱体水桶内部的底面积等于长方体鱼缸内部的底面积。（π取3.14）
（1）长方体鱼缸内部的长和高分别是多少？
（2）水桶和鱼缸的容积分别是多少立方分米？

【思路点拨】（1）根据圆柱的体积公式：V＝Sh，长方体的体积公式：V＝Sh，如果圆柱和长方体的体积相等，底面积也相等，那么它们的高一定相等，根据圆的面积公式：S＝πr2，长方形的面积公式S＝ab，那a＝S÷b，把数据代入公式解答。
（2）根据圆柱的容积公式：V＝Sh，把数据代入公式解答。
【规范解答】解：（1）3.14×202÷20
＝3.14×400÷20
＝1256÷20
＝62.8（厘米）
答：长方体鱼缸内部的长是62.8厘米，高是40厘米。
（2）3.14×202×40
＝3.14×400×40
＝1256×40
＝50240（立方厘米）
50240立方厘米＝50.24立方分米
答：水桶和鱼缸的容积都是50.24立方分米。
【考点评析】此题主要考查圆的面积公式、长方形的面积公式的灵活运用，圆柱的容积公式、长方体的容积公式的灵活运用，关键是熟记公式。
考点6：圆柱的侧面积、表面积和体积
【典例分析11】（2023•黄梅县模拟）早在三千多年前，我国传统典籍《周易》就提出了平均数的思想：“君子以哀多益寡，称物平施。”例如：4个同样的杯子装同一种水，杯子中水面的高度分别是18厘米、14厘米、16厘米和12厘米。每一个杯子中水面的高度为 　15　厘米时，这4个杯子中的水才同样多。
【思路点拨】根据求平均数的方法，求出个杯子里水面的总高度，然后除以杯子的个数，即可解答。
【规范解答】解：（18+14+16+12）÷4
＝60÷4
＝15（厘米）
答：每一个杯子中水面的高度为15厘米时，这4个杯子中的水才同样多。
故答案为：15。
【考点评析】解答这类应用题时，主要是弄清楚总数量、份数、平均数三量之间的关系。
【典例分析12】（2023•鄂州模拟）﹣张长80厘米，宽15厘米的长方形卡纸，围成一个圆柱纸筒，它的侧面积是1200平方厘米。　√　（判断对错）
【思路点拨】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形，这个长方形的长等于圆柱的底面周长，宽等于圆柱的高。根据圆柱的侧面积公式：S＝Ch，把数据代入公式求出这个圆柱的侧面积，然后与1200平方厘米进行比较。
【规范解答】解：80×15＝1200（平方厘米）
所以，这个圆柱的侧面积是1200平方厘米。
因此，题干中的计算是正确的。
故答案为：√。
【考点评析】此题考查的目的是理解掌握圆柱侧面展开图的特征，以及圆柱侧面积公式的灵活运用，关键是熟记公式。
【随堂演练11】（2023•红安县模拟）一个高50厘米的圆柱形容器内，放有一个高为20厘米的长方体铁块。打开水龙头往容器内注水3分钟，水正好没过长方体顶面。再注水18分钟，水灌满了容器。容器的底面积与长方体底面积的比是多少？
【思路点拨】由题意可知3分钟注入的水的体积＝长方体铁块的长×圆形形容器与长方体铁块的底面积之差；18分钟注入的水的体积＝圆形形容器的底面积×（50﹣20）；每分钟的注水量不变，结合上步分析可得20（S柱﹣S长）：30S柱＝1：6，结合比例的性质求出S柱：S长即可。
【规范解答】解：3分钟注入的水的体积＝（S柱﹣S长）×20
18分钟注入的水的体积＝（50﹣20）S柱＝30S柱
20（S柱﹣S长）：30S柱＝3：18＝1：6
30S柱＝120S柱﹣120S长
90S柱＝120S长
S柱：S长＝120：90＝4：3
答：容器的底面积与长方体底面积的比是4：3。
【考点评析】此题数量关系比较复杂，解题的关键是根据灌水时间关系来进行分析解答，这样就化难为简。
【随堂演练12】（2023•红安县模拟）一张长方形铁皮，按照如图剪下阴影部分，制成一个底面直径为4dm圆柱状的油漆桶，求它的容积（铁皮厚度忽略不计）．

【思路点拨】根据图形求出底面的半径，然后根据圆柱的体积公式：V＝πr2h，代入数值计算即可。
【规范解答】解：底面半径为：8÷4＝2（dm）
底面周长为：2×3.14×2＝12.56（dm）
长方形的长为：
16.56﹣2×2
＝16.56﹣4
＝12.56（dm）
所以，长方形的长是底面周长，宽就是圆柱的高，
它的容积为：
3.14×2×2×8
＝6.28×2×8
＝12.56×8
＝100.48（dm3）
100.48dm3＝100.48L
答：它的容积为100.48L。
【考点评析】本题主要考查了圆柱的体积公式，根据图形判断出圆柱的高为多少，是本题解题的关键。
考点7：圆锥的体积
【典例分析13】（2023•黔江区模拟）把一块长为9dm、宽为3.14dm、高为4dm的长方体钢块熔铸成一个底面直径是12dm的圆锥形钢坯，这个圆锥形钢坯的高是多少分米？
【思路点拨】根据体积的意义，把长方体钢块熔铸成圆锥形钢坯，体积不变，根据长方体的体积公式：V＝abh，圆锥的体积公式：V＝Sh，那么h＝V÷÷S，把数据代入公式解答。
【规范解答】解：9×3.14×4÷÷[3.14×（12÷2）2]
＝28.26×4÷÷[3.14×36]
＝113.04×3÷113.04
＝339.12÷113.04
＝3（分米）
答：这个圆锥形钢坯的高是3分米。
【考点评析】此题主要考查长方体的体积公式、圆锥的体积公式的灵活运用，关键是熟记公式。
【典例分析14】计算下面图形的体积。（单位：m）

【思路点拨】（1）根据图意可知，由此利用圆柱的体积公式：圆柱的体积＝底面积×高，代入数据计算即可解答；
（2）根据图意可知，由此利用圆锥的体积公式：圆锥体积＝×底面积×高，将所给数据分别代入相应的公式，即可解答。
【规范解答】解：（1）3.14×22×5
＝3.14×20
＝62.8（立方米）
（2）3.14×（6÷2）2×7×
＝3.14×21
＝65.94（立方米）
答：圆柱体积62.8立方米，圆锥体积65.94立方米。
【考点评析】此题考查了圆柱的体积公式和圆锥的体积公式的计算应用，要求学生熟记公式即可解答。
【随堂演练13】（2023•市中区模拟）一个圆锥体量得底面直径是12厘米，沿直径剖成两半后，（如图），表面积增加了120平方厘米，求原来圆锥体的体积是多少立方厘米？

【思路点拨】通过观察图形可知，把这个圆锥沿直径剖成两半，剖面是三角形，这个三角形的底等于圆锥的底面直径，三角形的高等于圆锥的高，据此可以求出圆锥的高，然后根据圆锥的体积公式：V＝πr2h，把数据代入公式解答。
【规范解答】解：120÷2＝60（平方厘米）
60×2÷12＝10（厘米）
3.14×（12÷2）2×10
＝3.14×36×10
＝376.8（立方厘米）
答：原来圆锥的体积是376.8立方厘米。
【考点评析】此题主要考查圆锥体积公式的灵活运用，关键是求出圆锥的高。
【随堂演练14】（2022•高明区）（1）求圆锥的体积。（单位：cm）
（2）求阴影部分的面积。（单位：m）


【思路点拨】（1）根据圆锥的体积公式：V＝πr2h，把数据代入公式解答。
（2）阴影部分的面积等于长方形的面积减去以3m为半径的半圆的面积，根据长方形的面积＝长×宽，圆的面积＝π×半径的平方，代入数据解答即可。
【规范解答】解：（1）×3.14×（6÷2）2×9
＝9.42×9
＝84.78（立方厘米）
答：圆锥的体积是84.78立方厘米。
（2）7×3﹣3.14×32÷2
＝21﹣28.26÷2
＝21﹣14.13
＝6.87（平方米）
答：阴影部分的面积是6.87平方米。
【考点评析】此题主要考查圆锥的体积公式、长方形的面积公式、圆的面积公式的灵活运用，关键是熟记公式

基础练
一．选择题（共5小题）
1．下列现象属于旋转的是（　　）
A．滑动手机解锁 B．苹果从树上掉落
C．拧水龙头
【思路点拨】旋转：在平面内，将一个图形绕一点按某个方向转动一定的角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。旋转前后图形的位置和方向改变，形状、大小不变。与时针转动方向相同的是顺时针旋转，反之就是逆时针旋转。
【规范解答】解：拧水龙头属于旋转。
故选：C。
【考点评析】此题考查了旋转的意义及在实际当中的运用。
2．（2023•红安县模拟）一个圆柱与一个圆锥等底等高，已知圆柱的体积比圆锥的体积多9立方米，圆锥的体积是（　　）立方米．
A．4.5 B．3 C．9
【思路点拨】因为等底等高的圆柱的体积是圆锥体积的3倍，所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的（3﹣1）倍，根据已知一个数的几倍是多少，求这个数，用除法解答．
【规范解答】解：9÷（3﹣1）
＝9÷2
＝4.5（立方米），
答：圆锥的体积是4.5立方米．
故选：A．
【考点评析】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用．
3．（2022春•六盘水期末）飞飞将一个等腰直角三角形连续旋转3次后得到如图，等腰直角三角形每次旋转的角度是（　　）

A．120° B．90° C．60° D．45°
【思路点拨】根据旋转的性质，观察图形，中心角是由4个度数相等的角组成，结合周角是360°求得每次旋转的度数。
【规范解答】解：360°÷4＝90°
则等腰直角三角形每次旋转的角度是90°。
故选：B。
【考点评析】本题把一个周角是360°和图形的旋转的特点结合求解。注意结合图形解题的思想。
4．（2022秋•西华县期末）一个圆柱从侧面看可以是（　　）
A．圆 B．长方形 C．三角形
【思路点拨】圆柱就是由两个大小相同的圆和一个侧面组成的，它的底面是完全相同的两个圆，侧面是一个曲面，据此判断。
【规范解答】解：圆柱的侧面沿高展开后会得到一个长方形或者正方形，所以一个圆柱从侧面看可以是长方形。
故选：B。
【考点评析】本题考查了圆柱的特征及认识。
5．（2022春•兴仁市期中）如图是圆柱展开图的是（　　）（单位：厘米）
A． B．
C． D．
【思路点拨】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形，这个长方形的长等于圆柱的底面周长，宽等于圆柱的高．根据圆的周长公式：C＝πd，把数据分别代入公式求出各圆柱的底面周长，然后进行比较即可。
【规范解答】解：A.3.14×3＝9.42，不符合题意；
B.3.14×3＝9.42，符合题意；
C.3.14×4＝12.56，不符合题意；
D.3.14×3＝6.28，不符合题意。
故选：B。
【考点评析】此题考查的目的是理解掌握圆柱展开图的特征及应用。
二．填空题（共3小题）
6．（2023•黄州区模拟）一个底面积为8.7平方分米，高为1分米的圆柱体铜坯，能铸成和它等底等高的圆锥体　3　个，每个圆锥体的体积是　2.9　立方分米。
【思路点拨】第1个空，圆柱的体积等于与它等底等高的圆锥体积的3倍，由此填空即可；第2个空，根据圆锥体积计算公式：圆锥体积＝×底面积×高，由此计算即可。
【规范解答】解：×8.7×1＝2.9（立方分米）
故一个底面积为8.7平方分米，高为1分米的圆柱体铜坯，能铸成和它等底等高的圆锥体3个，每个圆锥体的体积是2.9立方分米。
故答案为：3；2.9。
【考点评析】本题考查圆柱和圆锥的体积，需要掌握等底等高的圆柱与圆锥的关系。
7．（2022春•沽源县期中）一个圆柱形蛋糕盒要用丝带捆扎起来（如图），打结处需要6dm的丝带。捆扎好这个蛋糕盒，至少需要 　38　dm的丝带。

【思路点拨】通过观察图形可知：需要丝带的长度＝这个圆柱底面直径的4倍+高的4倍+打结用的长度，据此列式解答。
【规范解答】解：5×4+3×4+6
＝20+12+6
＝38（分米）
答：包扎这个蛋糕盒至少需要38分米长的丝带。
故答案为：38。
【考点评析】此题考查的目的是理解掌握圆柱的特征及应用，关键是弄清这个蛋糕是如何捆扎的。
8．（2022春•固始县期中）一个圆锥的体积是立方米，与它等底等高的圆柱体积是 　　立方米，如果圆锥的底面积是平方米，它的高是 　2　米。
【思路点拨】等底等高的圆柱的体积是圆锥体积的3倍，用圆锥的体积乘3就是与它等底等高的圆柱体积；圆锥的高＝圆锥的体积×3÷底面积，据此解答。
【规范解答】解：＝（立方米）
＝2（米）
答：与它等底等高的圆柱体积是立方米，如果圆锥的底面积是平方米，它的高是2米。
故答案为：；2。
【考点评析】此题主要考查等底等高的圆锥与圆柱体积之间关系的灵活运用。
三．计算题（共2小题）
9．（2022•峡江县）求图半圆柱的表面积。

【思路点拨】通过观察图形可知，它的表面积等于该圆柱侧面积的一半加上一个底面的面积，再加上一个切面（长方形）的面积，根据圆柱的侧面积公式：S＝πdh，圆的面积公式：S＝πr2，长方形的面积公式：S＝ab，把数据代入公式解答。
【规范解答】解：3.14×6×8÷2+3.14×（6÷2）2+8×6
＝150.72÷2+3.14×9+48
＝75.36+28.26+48
＝151.62（平方厘米）
答：半圆柱的表面积151.62平方厘米。
【考点评析】此题主要考查圆柱的侧面积公式、圆的面积公式的灵活运用，关键是熟记公式。
10．（2022春•龙港市期中）求圆锥的体积。

【思路点拨】根据圆锥的体积公式：V＝πr2h，把数据代入公式解答。
【规范解答】解：×3.14×32×6
＝×3.14×9×6
＝56.52（立方分米）
答：圆锥的体积是56.52立方分米。
【考点评析】此题主要考查圆锥体积公式的灵活运用，关键是熟记公式。
四．应用题（共5小题）
11．（2023•市中区模拟）有一台压路机的前轮是圆柱形，轮宽2米，直径是1.5米，前轮转动一周，压路的面积是多少平方米？
【思路点拨】压路机压路的面积实际上就是圆柱形滚筒的侧面积，要求转动一周压路的面积，就是求它的侧面积是多少，可利用侧面积公式S＝πdh列式解答。
【规范解答】解：3.14×1.5×2
＝3.14×3
＝9.42（平方米）
答：压路的面积是9.42平方米。
【考点评析】此题是求侧面积的实际应用，可利用侧面积公式S＝πdh来解答。
12．（2022春•辉县市期末）会议室内有2根长方体柱子，高3.5m，底面是边长为0.4m的正方形。如果给这些柱子四周贴上装饰纸，每平方米装饰纸的价格是80元，一共需要多少钱？（接头忽略不计）
【思路点拨】根据长方体的表面积公式：S＝2（ab+ah+bh），已知底面是边长0.4米的正方形，根据正方形的周长公式求出底面周长，然后用底面周长乘高即可求出涂漆的面积，再用涂漆的面积乘2求出两根柱子的面积，最后乘80即可。
【规范解答】解：0.4×4×3.5×2×80
＝1.6×7×80
＝11.2×80
＝896（元）
答：一共需要896元钱。
【考点评析】解答有关长方体计算的实际问题，一定要搞清所求的是什么，再进一步选择合理的计算方法进行计算解答问题。
13．（2022•南山区）一个圆锥形沙堆，它的底面半径是2m，高与底面半径的比是2：1，用这堆沙子在8m宽的公路上铺4cm厚的路面，能铺多少米？（π取3）
【思路点拨】根据圆锥的体积＝底面积×高÷3，长方体的体积＝长×宽×高，解答此题即可。
【规范解答】解：2×2＝4（米）
4厘米＝0.04米
3×2×2×4÷3÷（8×0.04）
＝16÷0.32
＝50（米）
答：能铺50米。
【考点评析】熟练掌握圆锥和长方体的体积公式，是解答此题的关键。
14．（2020•辽中区）一个圆柱形水池底面直径为10米，池深5米，如果在水池的底面和四周涂上水泥，涂水泥的面积是多少平方米？
【思路点拨】根据题意，涂水泥的面积即是这个圆柱形水池的表面积，圆柱形水池的表面积＝底面积+侧面积，利用圆的面积公式和圆柱的侧面积公式S＝底面周长×高进行计算即可得到答案。
【规范解答】解：3.14×10×5+3.14×（10÷2）2
＝157+78.5
＝235.5（平方米）
答：涂水泥的面积是235.5平方米。
【考点评析】此题主要考查圆柱的表面积公式在实际生活中的应用，熟记公式是解答本题的关键。
15．（2022春•长兴县期中）一个圆柱形水槽（如图），底面积是400cm2，内盛有12cm深的水。将一个棱长为8cm的正方体铁块放人水中（铁块完全浸没在水中，且水没有溢出），水面将上升到多少厘米？

【思路点拨】上升那部分水的体积与放入的正方体的体积相等，据此利用正方体的体积公式V＝a3求出上升水的体积，再除以容器的底面积即可求出水面上升的高度，再加上水的高度即可求出问题。
【规范解答】解：83＝512（立方厘米）
512÷400＝1.28（厘米）
1.28+12＝13.28（厘米）
答：水面将上升到13.28厘米。
【考点评析】解答此题的关键是理解正方体的体积等于上升水的体积。
提高练
一．选择题（共4小题）
1．（2023•黄梅县模拟）如果圆柱和圆锥的体积相等，高也相等，那么圆锥的底面积和圆柱的底面积的比是（　　）
A．1：3 B．3：1 C．1：1 D．1：2
【思路点拨】因为等底等高的圆柱的体积是圆锥体积的3倍，所以当圆柱与圆锥的体积相等，高也相等时，圆锥的底面积是圆柱底面积的3倍。据此解答。
【规范解答】解：当圆柱与圆锥的体积相等，高也相等时，圆锥的底面积是圆柱底面积的3倍。
所以圆锥的底面积和柱的底面积的比是3：1。
故选：B。
【考点评析】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
2．（2022•二七区）如图，圆锥（　　）的体积与这个圆柱相等。

A．A B．B C．C
【思路点拨】如果圆柱和圆锥的体积相等高也相等，那么圆锥的底面积就是圆柱的3倍；如果体积相等底面积也相等，圆锥的高就是圆柱高的3倍，由此解答即可。
【规范解答】解：A圆锥和圆柱的高相等，圆锥的底面积是圆柱的3倍，体积相等；
B圆锥和圆柱底面积相等，圆锥的高不是圆柱的3倍，体积不相等；
C圆锥和圆柱等底等高，圆锥体积是圆柱的。
故选：A。
【考点评析】此题主要根据圆柱和圆锥等体积等高，底面积之间的关系，及等体积等底面积，高之间的关系，来解决问题。
3．（2022春•云和县期中）底面积和高都相等的长方体和圆锥，它们的体积（　　）
A．它们的体积相等
B．长方体的体积是圆锥体积的
C．圆锥的体积是长方体体积的
D．圆锥的体积是长方体体积的3倍
【思路点拨】根据长方体的体积公式：V＝Sh，圆锥的体积公式：V＝Sh，据此解答即可。
【规范解答】解：底面积和高都相等的长方体和圆锥，圆锥的体积是长方体体积的。
故选：C。
【考点评析】此题主要考查长方体的体积公式、圆锥的体积公式的灵活运用，关键是熟记公式。
4．（2022•昌黎县）用一块长25.12厘米，宽18.84厘米的长方形铁皮，配上一块圆形铁片正好可以做成圆柱形容器。（单位：厘米）下面选项正确的是（　　）
A．r＝1 B．d＝3
C．d＝5 D．r＝4
【思路点拨】圆柱侧面沿高展开是一个长方形，长方形的长或宽是圆柱底面周长，分别求出各选项数据的圆的周长，只要与铁皮长或宽相等的即可。
【规范解答】解：A.3.14×1×2＝6.28（cm），不可以
B.3.14×3＝9.42（cm），不可以
C.3.14×5＝15.7（cm），不可以
D.3.14×4×2＝25.12（cm），可以。
故选：D。
【考点评析】关键是熟悉圆柱特征，知道侧面展开图长方形的长或宽就是圆柱的底面周长。
二．填空题（共4小题）
5．（2023•海淀区模拟）如图，将直角三角形以一条直角边所在的直线为轴旋转一周，可以得到一个圆锥，圆锥的底面直径是　8厘米或6厘米　，高是　3厘米或4厘米　。

【思路点拨】根据题意可知，如果以直角边（3厘米）为轴旋转一周，可以得到一个底面直径是（4×2）厘米，高是3厘米的圆锥；如果以直角边（4厘米）为轴旋转一周，可以得到一个底面直径是（3×2）厘米，高是4厘米的圆锥。据此解答即可。
【规范解答】解：4×2＝8（厘米）
3×2＝6（厘米）
答：圆锥的底面直径是8厘米或6厘米，高是3厘米或4厘米。
故答案为：8厘米或6厘米，3厘米或4厘米。
【考点评析】此题考查的目的是理解掌握圆锥的特征及应用。
6．（2022•管城区）陶陶准备制作一个圆柱体的低碳节能标志（如图），这个节能标志的表面积是 　251.2　平方厘米，体积是 　301.44　立方厘米。

【思路点拨】根据圆柱的底面直径是8厘米，高是6厘米，利用圆柱的侧面积＝底面周长×高，圆柱的表面积＝侧面积+底面积×2，圆柱的体积公式V＝πr2h代入数字计算即可。
【规范解答】解：8÷2＝4（厘米）
2×3.14×4＝25.12（厘米）
25.12×6+3.14×42×2
＝150.72+3.14×16×2
＝150.72+100.48
＝251.2（平方厘米）
3.14×42×6
＝50.24×6
＝301.44（立方厘米）
答：这个节能标志的的表面积是251.2平方厘米，体积是301.44立方厘米。
故答案为：251.2，301.44。
【考点评析】本题运用圆柱的侧面积、体积公式进行解答即可。
7．（2022春•云和县期中）等底等高的圆锥与圆柱的体积之和是36dm3，圆柱的体积是 　27立方分米　，圆锥的体积是 　9立方分米　。
【思路点拨】因为等底等高的圆柱的体积是圆锥体积的3倍，所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的（3+1）倍，根据已知一个数的几倍是多少，求这个数，用除法求出圆锥的体积，进而求出圆柱的体积。
【规范解答】解：36÷（3+1）
＝36÷4
＝9（立方分米）
9×3＝27（立方分米）
答：圆柱的体积是27立方分米，圆锥的体积是9立方分米。
故答案为：27立方分米，9立方分米。
【考点评析】此题考查目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
8．（2022•偃师市）李叔叔制作一个棱长12厘米的正方体密封盒。它的表面积是 　864　cm2，在盒内放入一个最大的圆柱，圆柱的底面积是 　113.04　πcm2；如果放入一个最大的圆锥，圆锥的体积是 　452.16　πcm3。
【思路点拨】根据正方体的表面积公式：S＝6a2，把数据代入公式求出正方体的表面积；在盒内放人一个最大的圆柱，也就是这个圆柱的底面直径和高都等于正方体的棱长，如果放入一个最大的圆锥，也就是这个圆锥与正方体等底等高，根据圆的面积公式：S＝πr2，圆锥的体积公式：V＝r2h，把数据代入公式解答。
【规范解答】解：12×12×6
＝144×6
＝864（平方厘米）
3.14×（12÷2）2
＝3.14×36
＝113.04（平方厘米）
3.14×（12÷2）2×12
＝3.14×36×12
＝452.16（立方厘米）
答：正方体的表面积是864平方厘米，圆柱的底面积是113.04平方厘米，圆锥的体积是452.16立方厘米。
故答案为：864；113.04；452.16。
【考点评析】此题主要考查正方体的表面积公式、圆的面积公式、圆锥的体积公式的灵活运用，关键是熟记公式。
三．计算题（共2小题）
9．（2022•曹县）做一个无盖的圆柱形水桶，有下面几种型号的铁皮可供搭配选择。（单位：dm）

我选择的是 　②　和 　③　搭配使用，请计算这个水桶的容积。
【思路点拨】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形，这个长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高，根据圆的周长公式：C＝πd或c＝2πr，把数据代入公式求出两个圆的周长，然后与两个长方形的长进行比较即可确定选择搭配。再根据圆柱的容积公式：V＝πr2h，把数据代入公式解答。
【规范解答】解：3.14×4＝12.56（分米）
2×3.14×3＝18.84（分米）
3.14×（4÷2）2×5
＝3.14×4×5
＝12.56×5
＝62.8（立方分米）
62.8立方分米＝62.8升
答：选择②和③搭配使用，这个水桶的容积是62.8升。
故答案为：②，③。
【考点评析】此题考查的目的是理解掌握圆柱展开图的特征及应用，圆柱容积公式的灵活运用，关键是熟记公式。
10．（2022•台儿庄区）图形计算。
（1）计算下面圆锥体的体积。

（2）如图，圆的面积是6.28dm2，求阴影部分（正方形）的面积。

【思路点拨】（1）根据圆锥的体积公式：V＝πr2h，把数据代入公式解答。
（2）通过观察图形可知，正方形的边长等于圆的半径，根据圆的面积公式：S＝πr2，把数据代入公式解答。
【规范解答】解：（1）3.14×32×8
＝3.14×9×8
＝75.36（立方分米）
答：这个圆锥的体积是75.36立方分米。
（2）设圆的半径为r分米，
3.14×r2＝6.28
3.14×r2÷3.14＝6.28÷3.14
r2＝1
答：阴影部分（正方形）的面积是1平方分米。
【考点评析】此题主要考查圆锥的体积公式、圆的面积公式、正方形的面积公式的灵活运用，关键是熟记公式。
四．应用题（共5小题）
11．（2023•铁山区模拟）一个近似于圆锥形的谷堆，它的底面半径是2米，高是0.6米。如果每立方米稻谷重1.2吨，这个谷堆大约重多少吨？
【思路点拨】根据圆锥的体积公式：V＝πr2h，把数据代入公式求出这堆稻谷的体积，然后用稻谷的体积乘每立方米稻谷的质量即可。
【规范解答】解：3.13×22×0.6×1.2
＝3.14×4×0.6×1.2
＝2.512×1.2
＝3.0144（吨）
答：这堆稻谷大约重3.0144吨。
【考点评析】此题主要考查圆锥体积公式的灵活运用，关键是熟记公式。
12．（2022春•房县期中）王师傅把一个底面直径是20厘米、高10厘米的圆柱体钢柱铸造成一个长方体，已知长方体的长是25厘米，宽是20厘米。它的高是多少厘米？
【思路点拨】根据圆柱体积＝底面积×高，求出钢柱体积，即长方体体积，再根据长方体的高＝体积÷长÷宽，列式解答即可。
【规范解答】解：3.14×（20÷2）2×10÷25÷20
＝3.14×100×10÷（25×20）
＝3140÷500
＝6.28（厘米）
答：它的高是6.28厘米。
【考点评析】此题主要考查圆柱的体积公式、长方体的体积公式的灵活运用，关键是熟记公式。
13．（2022•安次区）把底面直径是4cm，高是4cm的圆柱切开，再像如图这样拼起来，得到近似的长方体。

（1）在这个切拼的过程中，图形的表面积 　增加了　（填增加、减少或不变），增加（或减少）了多少cm2？
（2）图形的体积 　不变　（填增加、减少或不变），圆柱的体积是多少？
【思路点拨】（1）根据圆柱体积公式的推导过程可知，把一个圆柱切拼成一个近似长方体，体积不变，拼成分长方体的表面积比圆柱的表面积增加了两个切面的面积，每个切面的长等于圆柱的高，每个切面的宽等于圆柱的底面半径，根据长方形的面积公式：S＝ab，把数据代入公式解答。
（2）根据圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【规范解答】解：（1）4×（4÷2）×2
＝4×2×2
＝8×2
＝16（平方厘米）
所以在这个切拼的过程中，图形的表面积增加了，增加了16平方厘米。
（2）3.14×（4÷2）2×4
＝3.14×4×4
＝12.56×4
＝50.24（立方厘米）
所以图形的体积不变。圆柱的体积是50.24立方厘米。
故答案为：增加了；不变。
【考点评析】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用，圆柱表面积的意义、长方体表面积的意义及应用，圆柱的体积公式及应用。
14．（2022•安溪县）一个无盖的圆柱形铁皮桶，放入一个圆锥铁块，然后装满水。请根据问题选择需要的信息，进行解答。
①桶的底面直径6分米；
②桶的高5分米；
③圆锥的底面直径3分米；
④取出圆锥铁块后，水面距离桶沿3厘米。
（1）制作这个铁皮桶至少需要铁皮多少平方分米？
（2）圆锥铁块的体积是多少立方分米？
【思路点拨】（1）求制作这个铁皮桶至少需要铁皮多少平方分米，就是求圆柱的一个底面积与侧面积的和。
（2）用圆柱形铁皮桶装满水的体积减去取出圆锥铁块后水的体积即可。
【规范解答】解：（1）3.14×（）2+3.14×6×5
＝28.26+94.2
＝122.46（平方分米）
答：制作这个铁皮桶至少需要铁皮122.46平方分米。
（2）3.14×（）2×5﹣3.14×（）2×3
＝28.26×5﹣28.26×3
＝28.26×（5﹣3）
＝56.62（立方分米）
答：圆锥铁块的体积是56.52立方分米。
【考点评析】本题考查了圆柱体的表面积和圆锥的体积，需熟记公式，灵活应用。
15．（2022•淮上区）一个平面图形经过平移或旋转可以形成立体图形。例如，分别将长方形、圆作为底面，向上平移可以得到长方体、圆柱（如图1），它们的体积均可以用“底面积×高”进行计算；将一个长4厘米，宽3厘米的长方形，绕着长旋转一周，可以得到一个圆柱（如图2）。

（1）将一个底面直径 　6　厘米的圆作为底面，向上平移 　4　厘米，也可以形成图2中的圆柱。
（2）将一个两条直角边均为4厘米的直角三角作为底面，向上平移5厘米，形成一个立体图形（如图3），它体积是多少立方厘米？
【思路点拨】（1）根据点动成线、线动成面、面动成体，通过观察图形可知，图2的圆柱是由一个长4厘米，宽3厘米的长方形，绕着长旋转一周得到的，这个圆柱的底面半径是3厘米，高是4厘米，所以将一个底面直径是（3×2）厘米的圆作为底面，向上平移4厘米，也可以形成图2中的圆柱。
（2）根据柱体的体积公式：V＝Sh，把数据代入公式解答。
【规范解答】解：（1）3×2＝6（厘米）
将一个底面直径是6厘米的圆作为底面，向上平移4厘米，也可以形成图2中的圆柱。
（2）4×4÷2×5
＝16÷2×5
＝8×5
＝40（立方厘米）
答：它的体积是40立方厘米。
故答案为：6，4。
【考点评析】此题考查的目的是理解掌握面动成体的原理，以及柱体的体积公式及及应用。