第一单元《扇形统计图》（原卷版+解析版）——【期末复习】2022-2023学年六年级下册数学单元复习知识点+练习学案（苏教版）

这是一份第一单元《扇形统计图》（原卷版+解析版）——【期末复习】2022-2023学年六年级下册数学单元复习知识点+练习学案（苏教版），文件包含第一单元《扇形统计图》解析版期末复习2022-2023学年六年级下册数学单元复习知识点+练习学案苏教版docx、第一单元《扇形统计图》原卷版期末复习2022-2023学年六年级下册数学单元复习知识点+练习学案苏教版docx等2份学案配套教学资源，其中学案共58页， 欢迎下载使用。
2022-2023学年苏教版六年级下册同步重难点讲义精讲精练
第一单元 扇形统计图





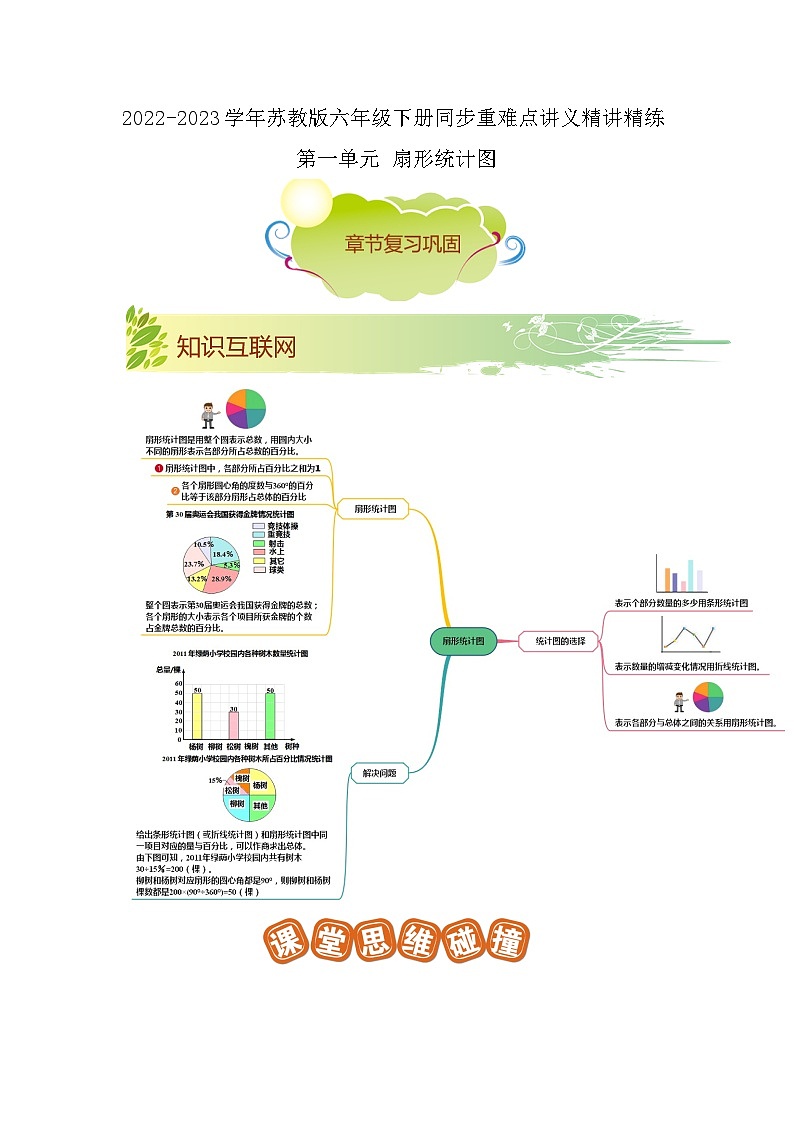
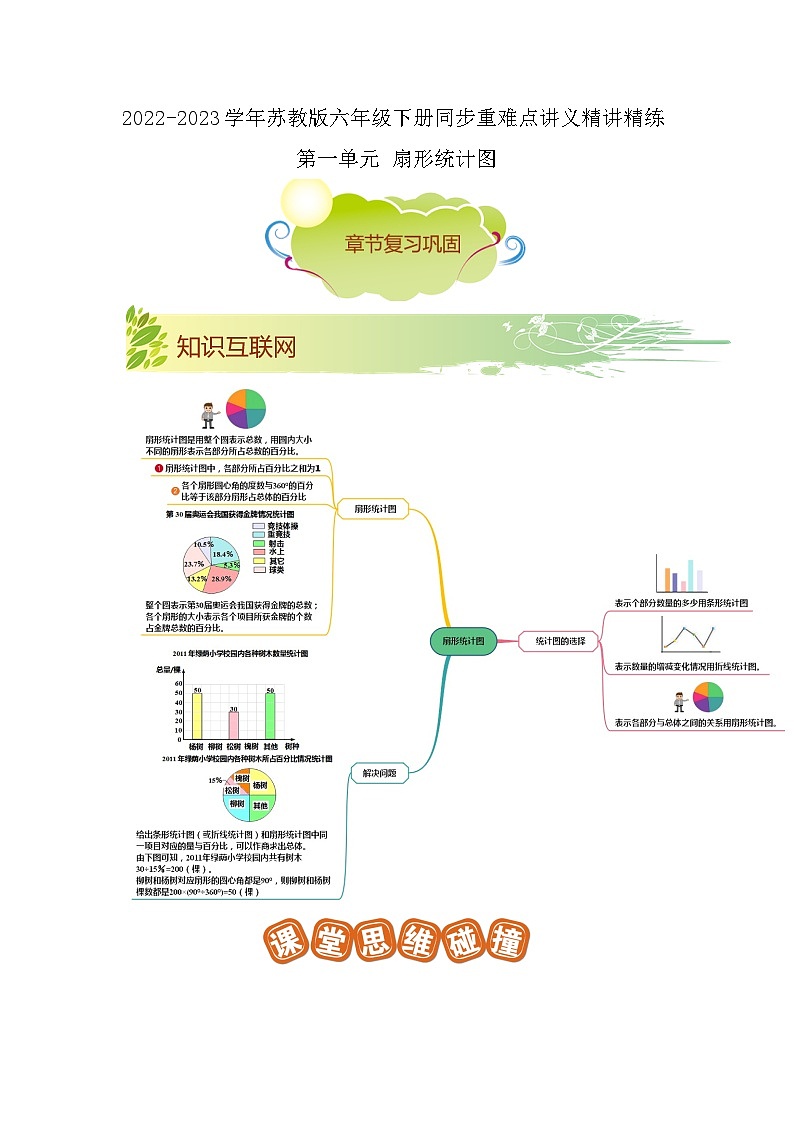
一、扇形统计图的意义：
用整个圆的面积表示总数，用圆内各个扇形面积表示各部分数量同总数之间的关系。也就是各部分数量占总数的百分比（因此也叫百分比图）。
二、常用统计图的优点：
1、条形统计图：可以清楚的看出各种数量的多少。
2、折线统计图：不仅可以看出各种数量的多少，还可以清晰看出数量的增减变化情况。
3、扇形统计图：能够清楚的反映出各部分数量同总数之间的关系。
三、扇形面积的大小表示的意义：
在同一个圆中，扇形的大小与这个扇形的圆心角的大小有关，圆心角越大， 扇形越大。（因此扇形面积占圆面积的百分比，同时也是该扇形圆心角度数占圆周角度数的百分比。）

考点1：扇形统计图的特点及绘制
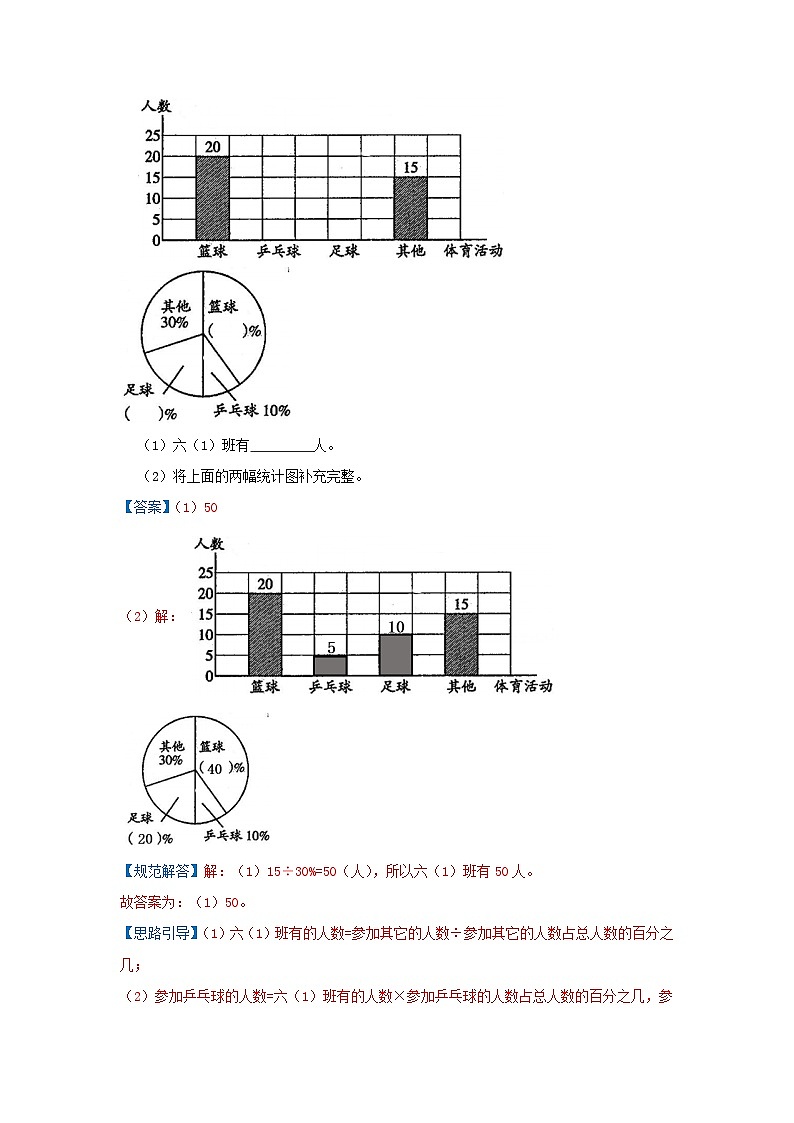
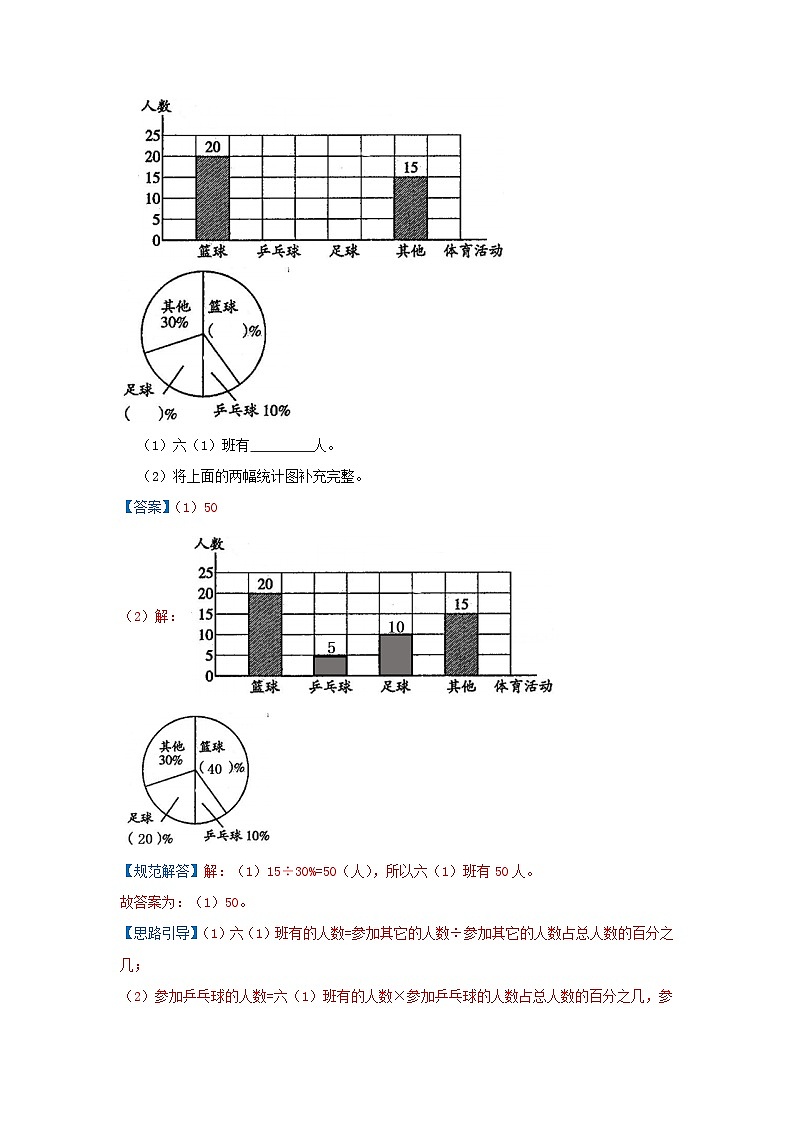
【典例分析01】（2022六上·惠州期中）为了响应中小学生每天锻炼1时的号召，兴达学校开展了形式多样的“阳光体育”活动，下面是在“阳光体育”活动中六（1）班全体同学参加各种体育活动的人数统计图。

（1）六（1）班有　 　人。
（2）将上面的两幅统计图补充完整。
【答案】（1）50
（2）解：
【规范解答】解：（1）15÷30%=50（人），所以六（1）班有50人。
故答案为：（1）50。
【思路引导】（1）六（1）班有的人数=参加其它的人数÷参加其它的人数占总人数的百分之几；
（2）参加乒乓球的人数=六（1）班有的人数×参加乒乓球的人数占总人数的百分之几，参加足球的人数=六（1）班有的人数-参加乒乓球的人数-参加其它的人数-参加篮球的人数，参加足球的人数占总人数的百分之几=参加足球的人数÷六（1）班有的人数，参加篮球的人数占总人数的百分之几=参加篮球的人数÷六（1）班有的人数。
【典例分析02】（2022·宝安）某校五一期间倡导四年级同学们积极参与家务劳动，为了解学生家务劳动情况，学校抽学部分学生进行问卷调查。如表是根据调查结果绘制的不完整的统计图（如图）

（1）请根据统计图中的信息将如表的统计表补充完整。
项目
经常做家务
偶尔做家务
从不做家务
调查总人数
占比
　 　
　 　
　 　
　 　
人数/人
　 　
30
　 　
（2）如果想了解经常做家务的孩子中最擅长做哪项家务，你有什么方法？
【答案】（1）50%；37.5%；12.5%；40；10；80
（2）解：将家务活分类，列统计表统计出每类有多少人即可。
【规范解答】解：（1）
项目
经常做家务
偶尔做家务
从不做家务
调查总人数
占比
50%
37.5%
12.5%
80
人数/人
40
30
10
故答案为：（1）50%；37.5%12.5%；80；40；10。
【思路引导】（1）从不做家务的占总人数的百分之几=100%-经常做家务的占总人数的百分之几-偶尔做家务的占总人数的百分之几；
调查的总人数=偶尔做家务的人数÷偶尔做家务的占总人数的百分之几；
经常做家务的人数=调查的总人数×经常做家务的占总人数的百分之几；
从不做家务的人数=调查的总人数×从不做家务的占总人数的百分之几；
（2）从分类统计的方法考虑即可。
【变式训练01】（2022·阳西）下列信息中，最适合用扇形统计图表示的是（　　）
A．小明6～12岁的身高变化 B．牛奶的营养成分
C．小红5次数学检测的成绩 D．某班男生的体重
【答案】B
【规范解答】解：最适合用扇形统计图表示的是牛奶的营养成分。
故答案为：B。
【思路引导】扇形统计图是用整个圆表示总数，用圆内各个扇形的大小表示各部分数量占总数的百分数；通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系。
【变式训练02】（2022·宁强）下面是实验小学六（3）班同学的期末体育成绩统计图，成绩按从高到低分为A，B，C，D四个等级，看图完成下列问题。

（1）补全上面的扇形统计图和条形统计图。
（2）六（3）班全班有　 　名学生。
（3）实验小学六（3）班同学的期末体育成绩C级人数比A级人数多　 　%。
【答案】（1）解：

（2）40
（3）60
【规范解答】解：（2）10÷25%=40名，所以六（3）班全班有40名学生；
（3）（16-10）÷10=60%，所以实验小学六（3）班同学的期末体育成绩C级人数比A级人数多60%。
故答案为：（2）40；（3）60。
【思路引导】（1）C级的人数占总人数的百分之几=100%-A级的人数占总人数的百分之几-C级的人数占总人数的百分之几-D级的人数占总人数的百分之几；一共有的人数=A级的人数÷A级的人数占总人数的百分之几，C级的人数=一共有的人数×C级的人数占总人数的百分之几；
（2）六（3）班全班有的人数=A等级的人数÷A等级的人数占总人数的百分之几；
（3）体育成绩C级人数比A级人数多百分之几=（C级人数-A级人数）÷A级人数。
考点2：统计图的选择
【典例分析03】实施“双减”政策后，为了调控作业量，班主任李老师要统计完成各科作业时间占完成作业总时间的百分比情况，她应选用（　　）
A．条形统计图 B．折线统计图 C．扇形统计图
【答案】C
【规范解答】解：她应选用扇形统计图。
故答案为：C。
【思路引导】条形统计图能清楚地看出数量的多少；折线统计图能清楚地看出数量的增减变化情况；扇形统计图能反应各个部分占总体的百分之几。
【典例分析04】（2023六上·海淀期末）下面是奇思记录的11月家庭支出情况。
奇思想绘制统计图表示11月各项家庭支出占总支出的百分比，他应选择（　　）。
奇思家11月家庭支出统计表
　
食品
服装
文化
水电气
赡养老人
其他
钱数/元
1440
400
800
400
640
320
占总支出的百分比
36%
10%
20%
10%
16%
8%
A．条形统计图 B．扇形统计图
C．折线统计图 D．复式折线统计图
【答案】B
【规范解答】解：他应选择扇形统计图。
故答案为：B。
【思路引导】条形统计图能清楚地看出数量的多少；折线统计图能清楚地看出数量的增减变化情况；扇形统计图能反应各个部分占总体的百分之几。
【变式训练03】星光小学2018 ~2021年在校学生人数情况统计表如下。
年份
2018
2019
2020
2021
人数
850
960
1200
1400
要表示在校学生人数的变化情况，选用　 　统计图比较合适。
【答案】折线
【规范解答】解：要表示在校学生人数的变化情况，选用折线统计图比较合适。
故答案为：折线。
【思路引导】条形统计图能清楚地看出数量的多少；折线统计图能清楚地看出数量的增减变化情况；扇形统计图能反应各个部分占总体的百分之几。
【变式训练04】某地在统计禽流感疫情时，既能知道雨天患病人数，又能反映疫情的变化情况和趋势，最好选用( )。
A．条形统计图 B．折线统计图 C．扇形统计图 D．统计表
【答案】B
【规范解答】折线统计图不仅能清楚反映出各种数量的多少，也可以直观反映出数量的增减变化情况。既能知道雨天患病人数，又能反映疫情的变化情况和趋势，最好选用折线统计图。
故答案为：B。
【思路引导】条形统计图能清楚地看出各种数量的多少；扇形统计图可以清楚地表示出各部分数量和总数量之间的关系。
考点3：统计图、统计表的综合应用
【典例分析05】（2022·殷都）六（2）班同学的几项数据用统计表和统计图表示如下：
六（2）班男、女生人数统计表
性别
男生
女生
合计
人数
27
　
　

（1）根据相关信息，把统计表和扇形统计图补充完整。
（2）参加　 　社团的男女生人数相等。参加跳绳社团的女生人数比男生少　 　人，参加跳绳社团的女生人数比男生少　 　%。
【答案】（1）解：
性别
男生
女生
合计
人数
27
23
50


（2）乐器；4；40
【规范解答】解：（1）27÷（1-46%）
=27÷54%
=50（人）
50-27=23（人）
（2）参加乐器社团的男女生人数相等；
10-6=4（人），参加跳绳社团的女生人数比男生少4人；
（10-6）÷10
=4÷10
=40%，参加跳绳社团的女生人数比男生少40%。
故答案为：（2）乐器；4；40。
【思路引导】（1）合计人数=男生人数÷（1-男生占的百分率），女生人数=合计人数-男生人数；
（2）参加跳绳社团的女生人数比男生少的百分率=参加跳绳社团的男生人数-参加跳绳社团的女生人数；参加跳绳社团的女生人数比男生少的百分率=（参加跳绳社团的男生人数-参加跳绳社团的女生人数）÷参加跳绳社团的男生人数。
【典例分析06】（2019·中山）下面是根据六（1）班学生某次数学测试情况制作的统计表和统计图。

（1）六（1）班共有学生多少人？
（2）把上面的统计表和统计图填完整。
【答案】（1）解： 10÷20%
=10÷0.2
=50（人）
答：六（1）班共有学生50人。
（2）解：50×6%=50×0.06=3（人）；50×8%=50×0.08=4（人）；
1-8%-6%-20%=66%；50×66%=50×0.66=33（人）

【思路引导】（1）观察图表可知，分数段60至79的人数10人正好占全班总人数的20%，即分数段60至79的人数÷20%=全班总人数，据此代入数据即可求出全班总人数。
（2）从扇形统计图中获取信息，60分以下人数占全班总人数的6%，100分人数占全班总人数的8%，用总量×百分率=部分量，即可分别求出60分以下人数和100分人数。
整个圆表示单位“1”，分数段80至99人数占全班总人数的（1-8%-6%-20%）。
【变式训练05】（2018·浙江模拟）观察右边统计图，回答问题。

（1）丽丽从　 　岁～　 　岁这一年中，身高增长最快。
（2）　 　岁时，她的身高最接近标准身高。
（3）全国同龄女生18岁时的身高是163.5厘米，我预测丽丽18岁时的身高是　 　厘米。
（4）如果身高与标准身高相差4％以内均为正常，则丽丽16岁时的身高属于　 　级别。(填“正常”或“偏矮”)
（5）我还能发现的信息是：　 　
【答案】（1）9；10
（2）10
（3）160
（4）正常
（5）身高越高，长得越缓慢
【规范解答】解：(1)根据各个年龄段的数据可知，丽丽从9岁～10岁这一年中，身高增长最快；
(2)10岁时，他的身高与标准身高相差最小，因此最接近标准身高；
(3)丽丽的身高比标准身高稍微矮，所以，全国同龄女生18岁时的身高是163.5厘米，我预测丽丽18岁时的身高是160厘米；
(4)(162-158)÷162≈2.5%，2.5%