必修 第二册6.4 平面向量的应用授课课件ppt

这是一份必修 第二册6.4 平面向量的应用授课课件ppt，共31页。PPT课件主要包含了三角形面积公式，△ABC中的常用结论，sinC，－cosC等内容，欢迎下载使用。
1.理解三角形面积公式的推导过程，掌握三角形的面积公式.2.了解正弦、余弦定理在平面几何中的应用.3.掌握正弦、余弦定理与三角函数的综合应用.
某近海海域有若干海岛，现有三个岛屿A，B，C，利用激光测距可测得AC，BC的距离分别为6 km和4 km，且可以测出AC，BC的夹角为60°.
则岛屿A，B ， C组成的三角形水域的面积如何计算呢？
已知△ABC的两边a，b和角C，如何求△ABC的面积？
边b上的高h为asin C，
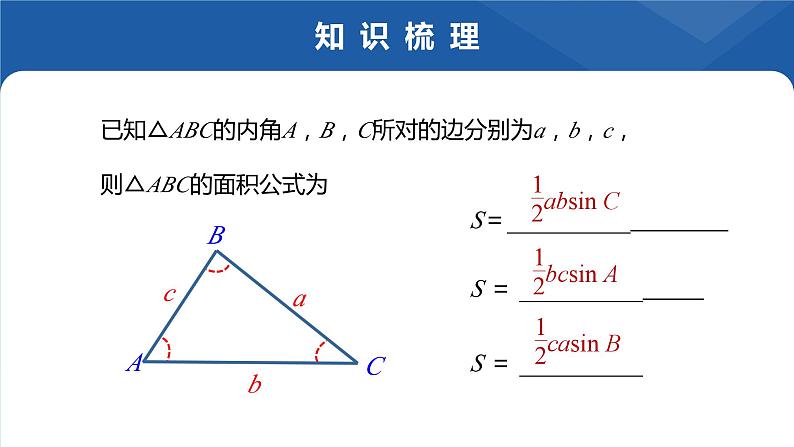
已知△ABC的内角A，B，C所对的边分别为a，b，c，
则△ABC的面积公式为
S＝__________ S ＝ __________ S ＝ __________
大边对大角，即a>b⇔A>B ⇔sin A>sin B.
A＋B＋C＝ ，sin(A＋B)＝ ，cs(A＋B)＝_______ .
解析　如图，结合题意绘出图象：
由正弦定理，得(2sin A－sin C)cs B＝sin Bcs C，∴2sin Acs B＝sin Bcs C＋sin Ccs B＝sin(B＋C)＝sin A，∵A∈(0，π)，∴sin A≠0，
即a2＋c2＝3＋ac≥2ac(当且仅当a＝c时取等号)，∴ac≤3，
方程思想在解题中的应用.
1.充分挖掘题目中的条件 2.转化为求两边及其夹角的正弦问题
如图，在△ABC中，D为边BC上一点，AD＝3，且sin∠ADB＝ sin B.
(2)若AD⊥AC，BC＝3BD，求△ABC的面积.
解　设BD＝m，由BC＝3BD，得DC＝2m，
在△ABD中，由余弦定理得，
又Rt△ADC中，AD＝3，
解得m2＝9，即m＝3，
AB2＝AD2＋BD2－2AD·BD·cs∠ADB，
余弦、正弦定理在平面几何中的应用
如图，在平面四边形ABCD中，∠DCB＝45°，DB⊥AD，CD＝2.
解　因为AD⊥DB，所以∠ADB＝90°，
所以sin∠DBC＝sin[π－(∠BCD＋∠BDC)]＝sin(∠BCD＋∠BDC)＝sin∠BCDcs∠BDC＋cs∠BCDsin∠BDC，
又A为锐角，所以A＝60°.
先找所求的边、角所在的三角形
再在三角形中通过余弦、正弦定理求边和角
(1)求sin C的值；
(2)若BD＝5，求△ABD的面积.
余弦、正弦定理与三角函数的综合应用
(1)求a和sin C的值；
又b－c＝2，解得b＝4，c＝2或b＝－2，c＝－4(舍去)，
∴由余弦定理，得a2＝b2＋c2－2bccs A
1.先由正弦、余弦定理求出内角正弦值、余弦值，再结合和、差、倍、半角公式可以求解问题中出现的三角函数值；
2. 先求函数的性质，再利用函数求角，解与三角形有关的问题.
在△ABC中，角A，B，C的对边分别为a，b，c.
所以cs B＝2sin B.
从而cs2B＝(2sin B)2，即cs2B＝4(1－cs2B)，
因为sin B>0，所以cs B＝2sin B>0，
1. 知识清单：(1)三角形的面积公式；(2)利用余弦、正弦定理解决平面几何问题；(3)余弦、正弦定理与三角函数的综合应用.
2. 方法归纳：化归转化、数形结合.3. 常见误区：利用余弦、正弦定理求值时会出现增根，易忽略检验.