2023年上海市虹口区中考数学二模试卷（含解析）

2023年上海市虹口区中考数学二模试卷

一、选择题（本大题共6小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）

1.  的相反数是(    )

A.  B.  C.  D.

2.  方程的解是(    )

A.  B.  C.  D.

3.  已知正比例函数的图象经过第二、四象限，那么的取值范围是(    )

A.  B.  C.  D.

4.  某地统计部门公布最近年居民消费价格指数年增长率分别为、、、和，业内人士评论说：“这年居民消费价格指数年增长率相当平稳”从统计角度看，“年增长率相当平稳”说明这组数据比较小的量是(    )

A. 方差 B. 平均数 C. 众数 D. 中位数

5.  下面用数学家名字命名的图形中，既是轴对称图形，又是中心对称图形的是(    )

A.     赵爽弦图 B.   笛卡尔心形线
C.     科克曲线 D.   斐波那契螺旋线

6.  如图，在矩形中，对角线与相交于点，，分别以点、为圆心画圆，如果与直线相交、与直线相离，且与内切，那么的半径长的取值范围是(    )

A.  B.  C.  D.

二、填空题（本大题共12小题，共48.0分）

7.  ______．

8.  ______．

9.  如果关于的一元二次方程有实数根，那么的取值范围是______．

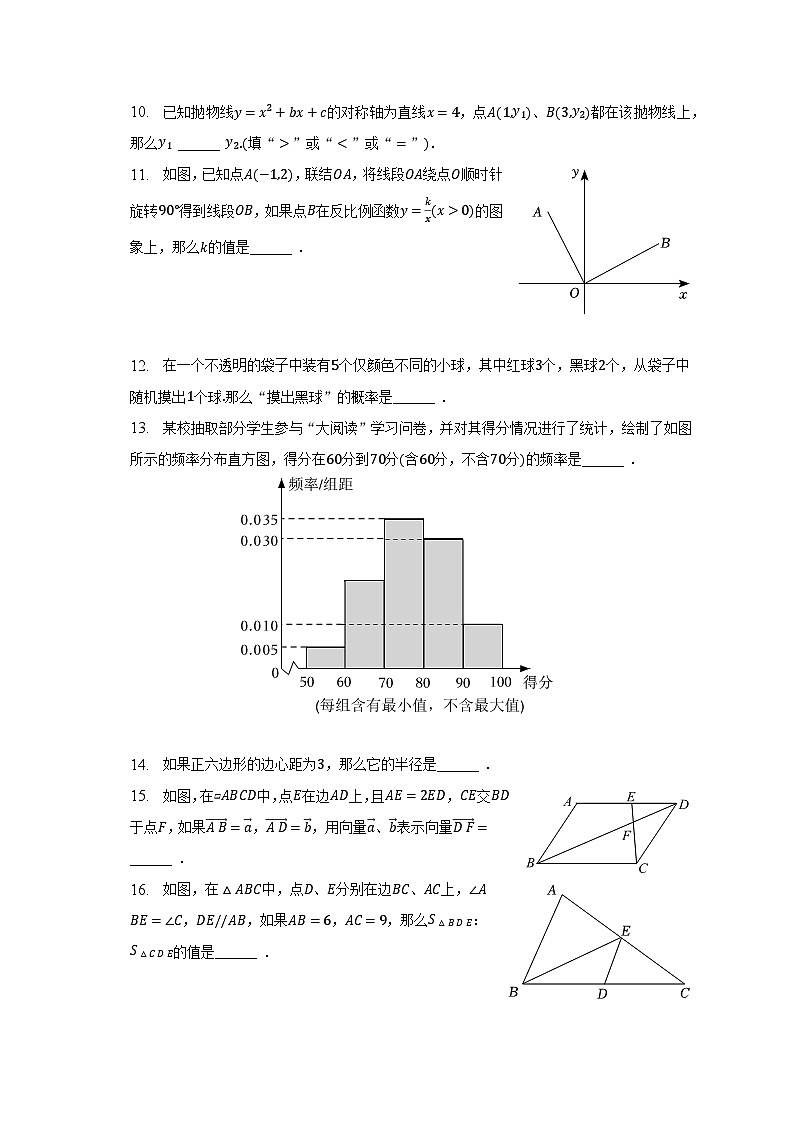
10.  已知抛物线的对称轴为直线，点、都在该抛物线上，那么 ______ 填“”或“”或“”．

11.  如图，已知点，联结，将线段绕点顺时针旋转得到线段，如果点在反比例函数的图象上，那么的值是______ ．

12.  在一个不透明的袋子中装有个仅颜色不同的小球，其中红球个，黑球个，从袋子中随机摸出个球那么“摸出黑球”的概率是______ ．

13.  某校抽取部分学生参与“大阅读”学习问卷，并对其得分情况进行了统计，绘制了如图所示的频率分布直方图，得分在分到分含分，不含分的频率是______ ．

14.  如果正六边形的边心距为，那么它的半径是______ ．

15.  如图，在▱中，点在边上，且，交于点，如果，，用向量、表示向量 ______ ．

16.  如图，在中，点、分别在边、上，，，如果，，那么：的值是______ ．

17.  我国古代著作四元玉鉴记载“买椽多少”问题：“六贯二百一十钱，请人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意：现请人代买一批椽，这批椽的价钱为文．如果每株椽的运费是文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问文能买多少株椽？若设这批椽的数量为株，则可列分式方程为______．

18.  如图，在矩形中，，点在边上，，联结，将沿着翻折，点的对应点为，联结、，分别交边于点，，如果，那么的长是______ ．

三、解答题（本大题共7小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

19.  本小题分
先化简，再求值：，其中．

20.  本小题分
解方程组：．

21.  本小题分
某商店以元千克的单价进货了一批商品，经调查发现，每天的销售量千克与销售单价元千克之间的函数关系如图中线段所示．
求与的函数表达式；
要使每天的销售利润达到元，销售单价应定为每千克多少元？

22.  本小题分
如图，在中，，，小明根据下列步骤作图：
以点为圆心，的长为半径作弧，交的延长线于点；
以点为圆心，取定长为半径作弧分别交的两边于点、；
以点为圆心，为半径作弧，交于点；
以点为圆心，的长为半径作弧，交前弧于点，联结并延长交的延长线于点．
填空：
由作图步骤可得，
由作图步骤可得______ ______ ，
又因为，
所以≌，理由是______ ．
联结，求的值．

23.  本小题分
如图，在梯形中，，，点为延长线上一点，，点在上，联结．
求证：；
如果，求证：四边形为梯形．

24.  本小题分
在平面直角坐标系中，已知抛物线的顶点为，与轴相交于点，异于顶点的点在该抛物线上．
如图，点的坐标为．
求点的坐标和的值；
将抛物线向上平移后的新抛物线与轴的一个交点为，顶点移至点，如果四边形为平行四边形，求平移后新抛物线的表达式；
直线与轴相交于点，如果且点在线段上，求的值．
 

25.  本小题分
如图，在菱形中，，点在对角线上，，是的外接圆，点与点之间的距离记为．
如图，当时，联结，求证：；
延长交射线于点，如果是直角三角形，求的长；
当圆心在菱形外部时，用含的代数式表示的半径，并直接写出的取值范围．

答案和解析

1.【答案】 

【解析】解：的相反数是．
故选：．
根据只有符号不同的两个数互为相反数，可得答案．
本题考查了实数的性质，在一个数的前面加上负号就是这个数的相反数．
 

2.【答案】 

【解析】解：，
方程两边平方得：，
解得：，
经检验是原方程的解，
故选：．
方程两边平方得出，求出方程的解，再进行检验即可．
本题考查了无理方程，能把无理方程转化成有理方程是解此题的关键，注意：解无理方程一定要检验．
 

3.【答案】 

【解析】解：正比例函数的图象经过第二、四象限，
比例系数，
．
故选：．
根据正比例函数的图象经过第二、四象限列出关于的不等式，求出的取值范围即可．
本题考查了正比例函数的性质，正比例函数，时，图象过第一、三象限；时，图象过第二、四象限．
 

4.【答案】 

【解析】解：根据方差的意义知，数据越稳定，说明方差越小．
故选：．
根据方差的意义：是反映一组数据波动大小，稳定程度的量；方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．故从统计角度看，“增长率相当平稳”说明这组数据方差比较小．
本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
 

5.【答案】 

【解析】解：是中心对称图形，但不是轴对称图形；不符合题意；
B.是轴对称图形，但不是中心对称图形；不符合题意；
C.既是轴对称图形，也是中心对称图形；符合题意；
D.既不是轴对称图形，也不是中心对称图形；不符合题意；
故选：．
根据轴对称图形和中心对称图形的定义即可作答．
本题主要考查了轴对称图形和中心对称图形的定义，熟练地掌握定义并能够区分轴对称图形和中心对称图形是解题的关键．
 

6.【答案】 

【解析】解：作于，于，
四边形是矩形，
，
，
是的中位线，

同理：，
设的半径是，
与直线相交、与直线相离，
，
由题意知，不然和不能内切，
，
，
两圆的圆心距，
，
，
，
．
故选：．
设的半径是，由与直线相交、与直线相离，得到；两圆的圆心距是、半径是和，两圆内切，由此即可求出的半径长的取值范围．
本题考查圆与圆的位置关系，矩形的性质，关键是掌握圆与圆的位置关系的判定方法．
 

7.【答案】 

【解析】解：原式．
故答案是：．
根据幂的乘方和同底数的幂的乘法运算法则即可求解．
本题考查了幂的乘方和同底数的幂的乘法运算法则，正确理解法则是关键．
 

8.【答案】 

【解析】

【分析】
本题考查了二次根式的性质与化简：也考查了绝对值的意义．
根据得到原式，然后根据绝对值的意义去绝对值即可．
【解答】
解：原式．
故答案为．  

9.【答案】 

【解析】

【分析】
此题考查了根的判别式，根的判别式的值大于，方程有两个不相等的实数根；根的判别式的值等于，方程有两个相等的实数根；根的判别式的值小于，方程没有实数根根据方程有实数根，得到根的判别式的值大于等于，列出关于的不等式，求出不等式的解集即可得到的范围．
【解答】
解：根据题意得：，
解得：．
故答案为．  

10.【答案】 

【解析】解：抛物线的对称轴为直线，，
当时，随着的增大而减小，
，
，
故答案为：．
首先利用对称轴和二次项系数的符号确定增减性，然后写出答案即可．
本题考查了二次函数的性质，解题的关键是根据题意确定增减性，难度不大．
 

11.【答案】 

【解析】解：点，
，，
线段是由线段绕点顺时针旋转得到的，
，，
又，，
，
≌，
，，
，
点在反比例函数的图象上，
．
故答案为：．
由旋转的性质，全等三角形的性质可得，，得到点的坐标，代入即可求出的值．
本题考查反比例函数函数图象上点的坐标特征，旋转的性质，求得点的坐标是解决问题的关键．
 

12.【答案】 

【解析】解：不透明的袋子中装有个仅颜色不同的小球，其中红球个，黑球个，
从袋子中随机摸出个球．那么“摸出黑球”的概率是．
故答案为：．
根据概率公式计算即可．随机事件的概率事件可能出现的结果数所有可能出现的结果数．
本题考查的是概率的求法．如果一个事件有种可能，而且这些事件的可能性相同，其中事件出现种可能，那么事件的概率．
 

13.【答案】 

【解析】解：由题意可知，得分在分到分含分，不含分的频率为，
故答案为：．
求出各个组的频率，再根据各组频率之和等于进行计算即可．
本题考查频率分布直方图，理解频率是正确解答的前提．
 

14.【答案】 

【解析】解：如图所示：

连接、，作于，
则，，，
，
设，则，
由勾股定理可得，，
解得：或舍去，
，
．
即它的半径为，
故答案为：．
连接、，作于，由正六边形的性质得出，，得出，由勾股定理求出，得出即可．
本题考查了正多边形和圆、正六边形的性质、勾股定理等知识；熟练掌握正六边形的性质，运用勾股定理求出是解决问题的关键．
 

15.【答案】 

【解析】解：在▱中，，
，
．
．
在▱中，，则，
．
．
，，
．
．
故答案为：．
根据平行四边形的性质和平行线截线段成比例求得的长度；然后利用三角形法则解答．
本题主要考查了平行四边形的性质和平面向量，掌握三角形法则和平面向量的方向是解题的关键．
 

16.【答案】 

【解析】解：，，
∽，
，
，
．
．
，
，
．
：．
故答案为：．
利用相似三角形的判定定理和性质定理求得线段的长，再利用平行线分线段成比例定理求得：的值，最后利用等高的三角形的面积比等于底的比的性质解答即可．
本题主要考查了相似三角形的判定与性质，平行线分线段成比例定理，等高的三角形的面积比等于底的比的性质，熟练掌握相似三角形的判定是解题的关键．
 

17.【答案】 

【解析】解：设这批椽的数量为株，
由题意可得：，
故答案为：．
根据题意可知：株需要文，株的运费一株椽的价钱，从而可以列出相应的方程．
本题考查由实际问题抽象出分式方程，解答本题的关键是明确题意，列出相应的方程．
 

18.【答案】 

【解析】解：延长，交的延长线于点，如图，

，
，即，
，，
，
四边形为矩形，，
，，，
∽，
，即，
，
，
根据折叠的性质可得，，，，，
，
，
，
，
，
，
在中，，
，
，
，，，
，
，
，
，
∽，
，即，
．
故答案为：．
延长，交的延长线于点，由题意可得，，易得∽，则，求得，进而求得，由折叠可知，，，，利用平行线的性质得，于是，，因此，在中，根据勾股定理求得，则，，由等角的余角相等可推出，以此可证明∽，最后利用相似三角形的性质即可求解．
本题主要考查矩形的性质、相似三角形的判定与性质、折叠的性质、勾股定理，根据题意正确画出图形，熟练掌握折叠的性质是解题关键．
 

19.【答案】解：原式

，
当时，原式． 

【解析】根据分式的除法法则、减法法则把原式化简，把的值代入计算即可．
本题考查的是分式的化简求值，掌握分式的除法法则、减法法则是解题的关键．
 

20.【答案】解：由得，
，
或，
当时，
，
把代入得，
，
，
，
，
当时，
，
把代入得，
，
，
，


，
，
综上所述原方程组的解为 或． 

【解析】先将左边因式分解，得或，然后与联立成两个二元一次方程组即可求解．
本题考查了二元二次方程组的解法，关键是将分解因式，转化为二元一次方程组．
 

21.【答案】解：设与的函数表达式为，
将，代入，得：，
解得：，．
与的函数表达式为为．
根据题意得：，
整理得：，
解得：，．
答：销售单价应定为每千克元或元． 

【解析】观察函数图象找出点的坐标，利用待定系数法可求出与的函数表达式；
根据总利润每千克利润销售数量，即可得出关于的一元二次方程，解之即可得出结论．
本题考查了一元二次方程的应用以及一次函数的应用，解题的关键是：根据点的坐标，利用待定系数法求出一次函数关系式；找准等量关系，正确列出一元二次方程．
 

22.【答案】     

【解析】解：由作图步骤可得，
由作图步骤可得，
又因为，
所以≌，理由是，
故答案为：，，．
作于点，则，
由得，≌，
，，
，
，
，
，，
，
，
的值是．
由作图得，，而，即可根据全等三角形的判定定理“”证明≌，于是得到问题的答案；
作于点，由得，≌，则，，所以，则，由勾股定理得，则，，可求得，所以．
此题重点考查尺规作图、全等三角形的判定与性质、勾股定理、锐角三角函数与解直角三角形等知识，正确地作出所需要的辅助线是解题的关键．
 

23.【答案】证明：在梯形中，，，
．
在和中，
，
≌，
，
，
．
，
，
∽．
，
；
∽，
，
．
，
，
，
，
∽，
，
，
，
，
，
．
又与不平行，
四边形为梯形． 

【解析】利用等腰梯形的性质和全等三角形的判定与性质得到，利用平行线的性质和相似三角形的判定与性质解答即可得出结论；
由的结论，利用等量代换的性质和相似三角形的判定与性质得到，利用平行线的性质，等量代换得到，则，再利用梯形的定义解答即可．
本题主要考查了等腰梯形的性质，梯形的判定，全等三角形的判定与性质，相似三角形的判定与性质，平行线的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．
 

24.【答案】解：点在抛物线上，
，
解得，
抛物线的表达式为，
，点是该抛物线的顶点，
；
点在抛物线上，
．
如图，四边形为平行四边形，
，，
将抛物线向上平移，
轴，
轴，
，
，
抛物线向上平移个单位，
，
平移后新抛物线的表达式为．
如图，抛物线，当时，；
当时，，
，；
，
，
设直线的表达式为，则，
，
，
当时，，
；
设直线的表达式为，则，
；
直线的表达式为，则，
，
，
，
，
解得，，
当时，则，
在线段上；
当时，则，
不在线段上，
不符合题意，舍去，
的值为． 

【解析】将代入，得，则，由，得；将代入，可求得；
由平行四边形的性质得，，因为轴，所以轴，则，可知抛物线向上平移了个单位，所以平移后新抛物线的表达式为；
先求得，，，可求得直线的表达式为，则；设直线的表达式为，则，得；设直线的表达式为，则，得，由得，即可求得符合题意的值为．
此题重点考查二次函数的图象与性质、一次函数的图象与性质、用待定系数法求函数表达式、平行四边形的判定与性质、一元二次方程的解法等知识与方法，此题综合性强，难度较大，属于考试压轴题．
 

25.【答案】证明：连接，交于点，如图，

，
，
又过圆心，
．
，
．
在菱形中，，
在中，
，
，
即，
；
解：，如果是直角三角形，那么只有或，
当时，
连接，如图，

由题可得：，，
在中，
，，
．
，
，
即：，
；
当时，

，
，
在菱形中，，
，
，
，
在中，
，
，
综上所述，或；
解：连接，过点作于点，延长交于点，过点作于点，如图，

，
，
同理，，
，，
，
，
．
在中，
，
．
在中，，
在中，
，
，
的半径为，
的取值范围为或． 

【解析】本题主要考查了菱形的性质，三角形的外接圆，圆的有关性质，圆周角定理，垂径定理，直角三角形的性质，勾股定理，直角三角形的边角关系定理，熟练掌握圆的有关性质和利用分类讨论的思想方法解答是解题的关键．
连接，交于点，利用垂径定理得到，再利用菱形的性质和直角三角形的性质解答即可；
由于，如果是直角三角形，那么只有或，利用分类讨论的方法解答：当时，连接，利用直角三角形的边角关系定理求得，，则，再利用平行线分线段成比例解答即可得出结论；当时，利用菱形的面积公式求得，再利用菱形的性质和而直角三角形的边角关系定理求得，则结论可求；
连接，过点作于点，延长交于点，过点作于点，利用垂径定理得到，，在中和在中，求得，，在中，利用勾股定理即可得出结论．