2023年山东省济南市平阴县中考数学二模试卷（含解析）

这是一份2023年山东省济南市平阴县中考数学二模试卷（含解析），共28页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
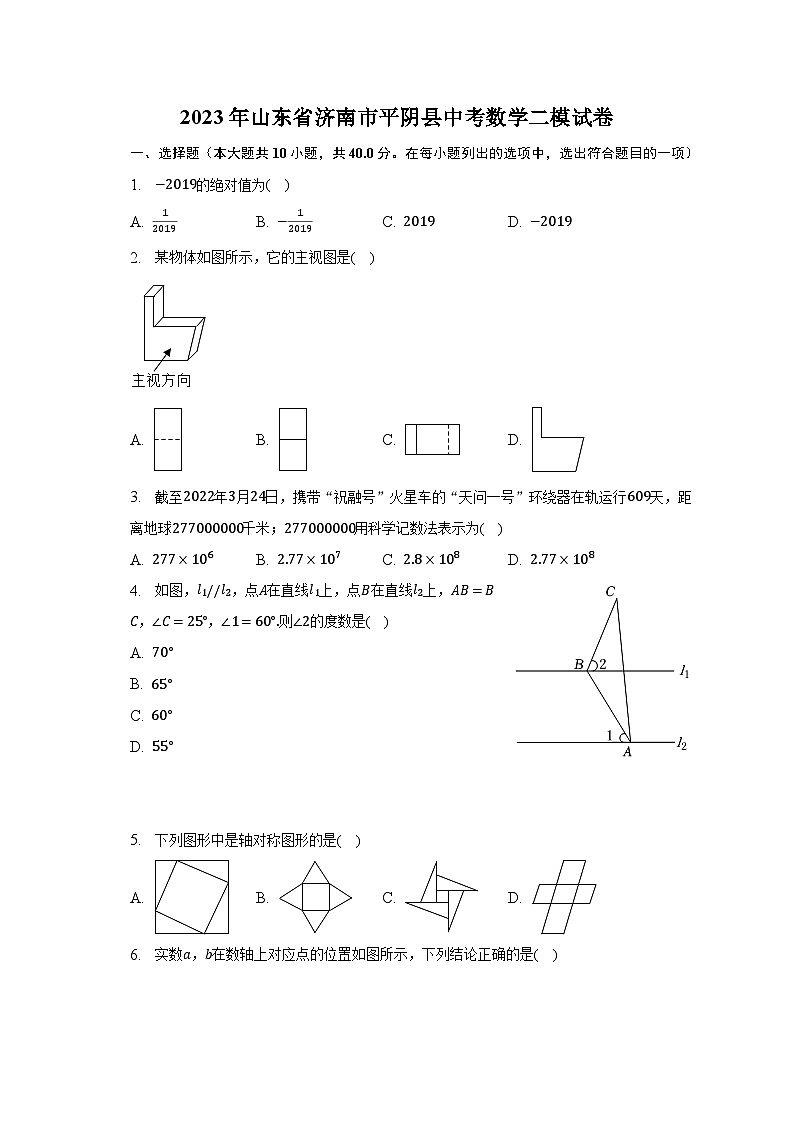
2023年山东省济南市平阴县中考数学二模试卷一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）1.  的绝对值为(    )A.  B.  C.  D. 2.  某物体如图所示，它的主视图是(    )
 A.  B.  C.  D. 3.  截至年月日，携带“祝融号”火星车的“天问一号”环绕器在轨运行天，距离地球千米；用科学记数法表示为(    )A.  B.  C.  D. 4.  如图，，点在直线上，点在直线上，，，则的度数是(    )A.
B.
C.
D.
 5.  下列图形中是轴对称图形的是(    )A.  B.  C.  D. 6.  实数，在数轴上对应点的位置如图所示，下列结论正确的是(    )
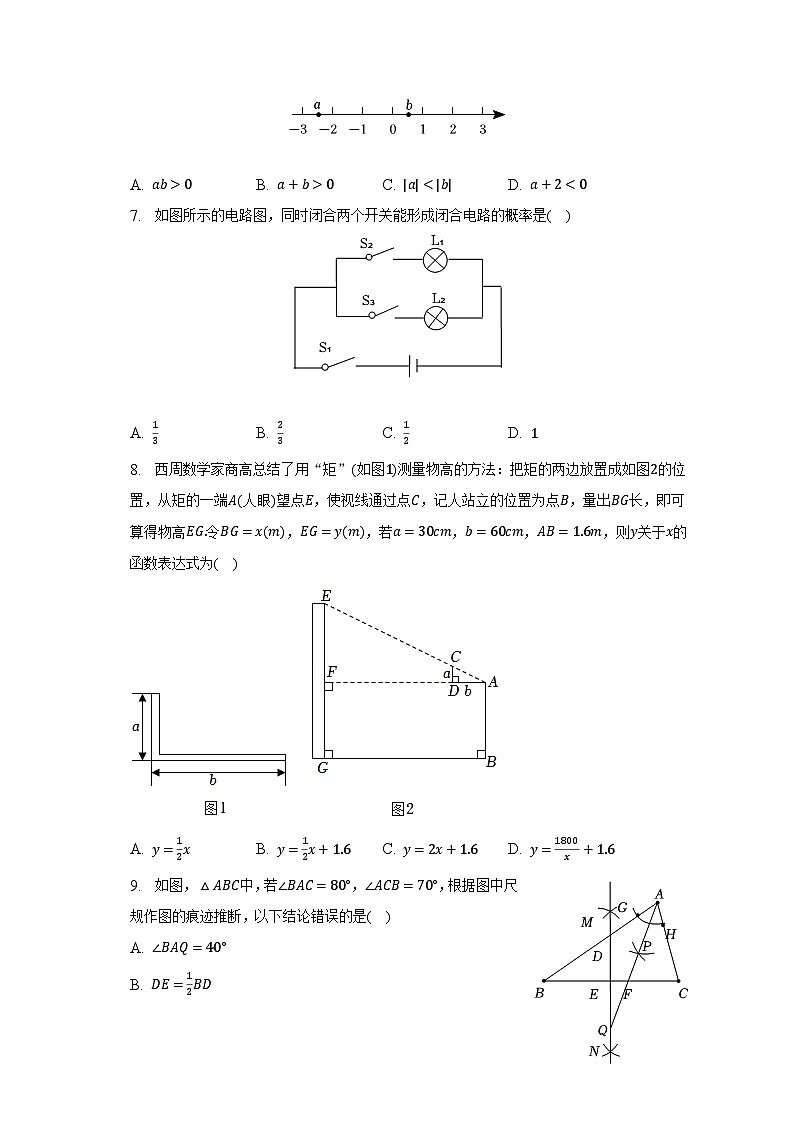
A.  B.  C.  D. 7.  如图所示的电路图，同时闭合两个开关能形成闭合电路的概率是(    )
A.  B.  C.  D. 8.  西周数学家商高总结了用“矩”如图测量物高的方法：把矩的两边放置成如图的位置，从矩的一端人眼望点，使视线通过点，记人站立的位置为点，量出长，即可算得物高令，，若，，，则关于的函数表达式为(    )
 A.  B.  C.  D. 9.  如图，中，若，，根据图中尺规作图的痕迹推断，以下结论错误的是(    )A.
B.
C.
D.
 10.  已知抛物线与轴有两个交点，，抛物线与轴的一个交点是，则的值是(    )A.  B.  C. 或 D. 或二、填空题（本大题共6小题，共24.0分）11.  分解因式：          ．12.  如图，小明向图中的格盘中随意投掷一枚棋子，该棋子落在三角形内的概率是______．
 13.  关于的一元二次方程的一个根是，则另一个根是______ ．14.  如图，在中，，，，分别为，，的中点．若的长为，则的长为______．
 15.  沐沐用七巧板拼了一个对角线长为的正方形，再用这副七巧板拼成一个长方形如图所示，则长方形的对角线长为______．
16.  如图，在平面直角坐标系中，把一个点从原点开始向上平移个单位，再向右平移个单位，得到点；把点向上平移个单位，再向左平移个单位，得到点；把点向下平移个单位，再向左平移个单位，得到点；把点向下平移个单位，再向右平移个单位，得到点，；按此做法进行下去，则点的坐标为______．
三、计算题（本大题共1小题，共6.0分）17.  计算：．四、解答题（本大题共9小题，共80.0分。解答应写出文字说明，证明过程或演算步骤）18.  本小题分
解不等式组：，并写出它的整数解．19.  本小题分
如图，在矩形中，点、分别是边、的中点．求证：．
20.  本小题分
年月日，“天宫课堂”第二课开讲“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课为了激发学生的航天兴趣，某校举行了太空科普知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分为如下组满分分，组：，组：，组：，组：，组：，并绘制了如下不完整的统计图请结合统计图，解答下列问题：

频数分布直方图中 ______ ，所抽取学生成绩的中位数落在______ 组；
补全学生成绩频数分布直方图；
若成绩在分及以上为优秀，学校共有名学生，估计该校成绩优秀的学生有多少人？21.  本小题分
每年的月日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图，架在消防车上的云梯可伸缩最长可伸至，且可绕点转动，其底部离地面的距离为，当云梯顶端在建筑物所在直线上时，底部到的距离为．
若，求此时云梯的长．
如图，若在建筑物底部的正上方处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．
参考数据：，，
 22.  本小题分
如图，是的直径，是的弦，平分交于点，过点作的切线，交的延长线于点，交的延长线于点．
求证：；
若，，，求的长．
23.  本小题分
阅读材料：被誉为“世界杂交水稻之父”的“共和国勋章”获得者袁隆平，成功研发出杂交水稻，杂交水稻的亩产量是普通水稻的亩产量的倍．现有两块试验田，块种植杂交水稻，块种植普通水稻，块试验田比块试验田少亩．
块试验田收获水稻千克、块试验田收获水稻千克，求普通水稻和杂交水稻的亩产量各是多少千克？
为了增加产量，明年计划将种植普通水稻的块试验田的一部分改种杂交水稻，使总产量不低于千克，那么至少把多少亩块试验田改种杂交水稻？24.  本小题分
如图，一次函数的图象与轴交于点，与反比例函数的图象交于点．
______ ； ______ ；
点是线段上一点不与，重合，过点作轴的平行线与该反比例函数的图象交于点，连接，，，当四边形的面积等于时，求点的坐标；
在的前提下，将沿射线方向平移一定的距离后，得到，若点的对应点恰好落在该反比例函数图象上如图，请直接写出此时点的对应点的坐标．25.  本小题分
【情境再现】
甲、乙两个含角的直角三角尺如图放置，甲的直角顶点放在乙斜边上的高的垂足处．将甲绕点顺时针旋转一个锐角到图位置．小莹用作图软件按图作出示意图，并连接，，如图所示，交于，交于，通过证明≌，可得．
请你证明：．

【迁移应用】
延长分别交，所在直线于点，，如图，猜想并证明与的位置关系．
【拓展延伸】
小亮将图中的甲、乙换成含角的直角三角尺，如图，按图作出示意图，并连接，，如图所示，其他条件不变，请你猜想并证明与的数量关系．26.  本小题分
如图，抛物线交轴于，两点，交轴于点，动点在抛物线的对称轴上．
求抛物线的解析式；
当以，，为顶点的三角形周长最小时，求点的坐标及的周长；
若点是平面直角坐标系内的任意一点，是否存在点，使得以，，，为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点的坐标；若不存在，请说明理由．

答案和解析 1.【答案】 【解析】【分析】此题主要考查了绝对值，正确把握绝对值的定义是解题关键．
直接利用绝对值的定义进而得出答案．
【解答】解：的绝对值是：．
故选：．  2.【答案】 【解析】解：某物体如图所示，它的主视图是：

故选：．
根据主视图的定义和画法进行判断即可．
本题考查简单几何体的主视图，主视图就是从正面看物体所得到的图形．
 3.【答案】 【解析】解：．
故选：．
科学记数法：把一个大于的数记成的形式，其中是整数数位只有一位的数，是正整数，这种记数法叫做科学记数法．【科学记数法形式：，其中，为正整数．】
本题主要考查了科学记数法表示较大的数，熟练掌握科学记数法表示较大的数的方法进行求解是解决本题的关键．
 4.【答案】 【解析】解：如图，

，，
，
，，
，
，
．
故选：．
利用等腰三角形的性质得到，利用平行线的性质得到，再根据三角形外角的性质即可求解．
本题考查了等腰三角形的性质，平行线的性质以及三角形外角的性质，解决问题的关键是注意运用两直线平行，同旁内角互补．
 5.【答案】 【解析】解：，，选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：．
直接利用轴对称图形的定义进行判断．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
此题主要考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 6.【答案】 【解析】解：由数轴可知，，
则，，，，故A，，不符合题意，符合题意．
故选D．
根据，两点在数轴上的位置上判断出其取值范围，再由有理数混合运算的法则进行判断即可．
本题考查的是实数与数轴，先根据题意判断出，的取值范围是解题的关键．
 7.【答案】 【解析】解：把、、分别记为、、，
画树状图如下：

共有种可能的结果，其中同时闭合两个开关能形成闭合电路的结果有种，即、、、．
所以同时闭合两个开关能形成闭合电路的概率为．
故选：．
画树状图，可知共有种可能的结果，其中同时闭合两个开关能形成闭合电路的结果有种，再由概率公式求解即可．
本题考查的是用树状图法求概率．树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件．用到的知识点为：概率所求情况数与总情况数之比．
 8.【答案】 【解析】解：由图可得，
，，，，
，
，，
，
∽，
，
即，
，
化简，得，
故选：．
根据题意和图形，可以得到，，，，然后根据相似三角形的性质，可以得到与的函数关系式．
本题考查一次函数的应用、相似三角形的判定与性质，解答本题的关键是明确题意，利用数形结合的思想解答．
 9.【答案】 【解析】解：由作图可知，平分，
，
故选项A正确，不符合题意；
B.由作图可知，是的垂直平分线，
，
，
，
故选项B正确，不符合题意；
C.，，
，
，
，
故选项C正确，不符合题意；
D.，，
；
故选项D错误，符合题意．
故选：．
根据线段的垂直平分线的性质，角平分线的定义，三角形外角的性质，直角三角形的性质判断即可．
本题考查了尺规作图作角的平分线及线段的垂直平分线，线段的垂直平分线的性质，角平分线的定义，三角形外角的性质，直角三角形的性质等知识，解题的关键是读懂图象信息．
 10.【答案】 【解析】解：抛物线的对称轴为直线，抛物线的对称轴为直线，
当点平移后的对应点为，则；
当点平移后的对应点为，则，
即的值为或．
故选：．
先利用二次函数的性质得到两抛物线的对称轴，然后利用点或点向右平移得到点得到的值．
本题考查了抛物线与轴的交点：把求二次函数是常数，与轴的交点坐标问题转化为解关于的一元二次方程．也考查了二次函数的性质．
 11.【答案】 【解析】【分析】
直接运用平方差公式分解因式即可．
本题主要考查平方差公式分解因式，掌握平方差公式的结构特点是解题的关键．
【解答】
解：．
故答案为：．  12.【答案】 【解析】解：三角形面积为，
正方形面积为，
故该棋子落在三角形内的概率是．
故答案为：．
利用面积公式分别表示出阴影部分和大正方形的面积，再利用面积比求概率即可．
本题主要考查几何概率，求概率时，已知和未知与几何有关的就是几何概率．计算方法是长度比，面积比，体积比等．
 13.【答案】 【解析】解：设另一个根为，由根与系数之间的关系得，
，
，
故答案为：，
利用根与系数之间的关系求解．
本题主要考查根与系数的关系，解题的关键是熟练运用根与系数的关系，本题属于基础题型．
 14.【答案】 【解析】解：，分别为，的中点，
是的中位线，
，
，
在中，，为中点，，
，
故答案为：．
根据三角形中位线定理求出，根据直角三角形斜边上的中线的性质即可求出．
本题考查了直角三角形斜边上的中线的性质以及三角形的中位线定理，求得的长是解本题的关键．
 15.【答案】 【解析】解：根据图形可知：长方形的长是正方形的对角线为，
长方形的宽是正方形对角线的一半为，
则长方形的对角线长．
故答案为：．
根据图形可得长方形的长是正方形的对角线为，长方形的宽是正方形对角线的一半为，然后利用勾股定理即可解决问题．
本题考查了正方形的性质，七巧板，矩形的性质，解决本题的关键是掌握正方形的性质．
 16.【答案】 【解析】解：由图象可知，，
将点向左平移个单位、再向上平移个单位，可得，
将点向左平移个单位，再向下平移个单位，可得，
将点向右平移个单位，再向下平移个单位，可得，
将点向右平移个单位，再向上平移个单位，可得，
将点向左平移平移个单位，再向上平移个单位，可得，
故答案为：．
根据题目规律，依次求出、的坐标即可．
本题主要考查了坐标与图形变化平移，规律型问题，解题的关键是学会探究规律，属于中考常考题型．
 17.【答案】解：原式

． 【解析】直接利用算术平方根以及零指数幂的性质、负整数指数幂的性质、特殊角的三角函数值分别化简得出答案．
此题主要考查了算术平方根以及零指数幂的性质、负整数指数幂的性质、特殊角的三角函数值，正确化简各数是解题关键．
 18.【答案】解：，
解不等式得：，
解不等式得：，
不等式组的解集是．
整数解为：，． 【解析】分别解出每个不等式，再求公共解集即可．
本题考查解不等式组，解题的关键是掌握求公共解集的方法．
 19.【答案】解：四边形是矩形，
，，
又、分别是边、的中点，
，
又，
四边形是平行四边形，
． 【解析】本题考查的是矩形的性质、平行四边形的判定和性质，掌握相关的判定定理和性质定理是解题的关键．根据矩形的性质和已知证明，，得到四边形是平行四边形，根据平行四边形的性质得到答案．
 20.【答案】   【解析】解：本次调查一共随机抽取的学生总人数为：名，
组的人数为：名，
，
所抽取学生成绩的中位数是第个和第个成绩的平均数，，
所抽取学生成绩的中位数落在组，
故答案为：，；
组的人数为：人，
补全学生成绩频数分布直方图如下：

人，
答：估计该校成绩优秀的学生有人．
由组的人数除以所占百分比得出本次调查一共随机抽取的学生数，用总人数乘以组的百分比即可求出的值，根据中位数的定义，即可解决问题；
求出组的人数，补全学生成绩频数分布直方图即可；
由学校共有学生人数乘以成绩优秀的学生所占的比例即可．
本题考查扇形统计图，频数分布直方图，用样本估计总体和中位数，从统计图中获取数量和数量关系是正确计算的前提．
 21.【答案】解：在中，，，
，
此时云梯的长为；
在该消防车不移动位置的前提下，云梯能伸到险情处，
理由：由题意得：
，
，
，
在中，，
，
，
在该消防车不移动位置的前提下，云梯能伸到险情处． 【解析】在中，利用锐角三角函数的定义求出的长，即可解答；
根据题意可得，从而求出，然后在中，利用锐角三角函数的定义求出的长，进行比较即可解答．
本题考查了解直角三角形的应用，熟练掌握锐角三角函数的定义是解题的关键．
 22.【答案】证明：连接，如图：

平分，
，
，
，
，
，
是的切线，是的半径，
，
；
解：连接并延长交于，连接，，如图：

是的直径，
，
，
，
，即，
，
，
，
，
，
，
，
∽，
，
，，
，
，
解得，
在中，，
，
平分，
，
，
，
，
答：的长为． 【解析】连接，由平分，，可得，而是的切线，是的半径，有，即得；
连接并延长交于，连接，，由是的直径，，可得，即可得，从而∽，，知，解得，根据，得，故，即得，可得．
本题考查圆的综合应用，涉及相似三角形判定与性质，锐角三角函数，圆的切线等知识，解题的关键是作辅助线，构造相似三角形解决问题．
 23.【答案】解：设普通水稻的亩产量是千克，则杂交水稻的亩产量是千克，
依题意得：，
解得：，
经检验，是原方程的解，且符合题意，
则．
答：普通水稻的亩产量是千克，杂交水稻的亩产量是千克；
设把亩块试验田改种杂交水稻，
依题意得：，
解得：．
答：至少把亩块试验田改种杂交水稻． 【解析】设普通水稻的亩产量是千克，则杂交水稻的亩产量是千克，利用种植亩数总产量亩产量，结合块试验田比块试验田少亩，即可得出关于的分式方程，解之即可得出普通水稻的亩产量，再将其代入中即可求出杂交水稻的亩产量；
设把亩块试验田改种杂交水稻，利用总产量亩产量种植亩数，结合总产量不低于千克，即可得出关于的一元一次不等式，解之取其中的最小值即可得出结论．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：找准等量关系，正确列出分式方程；根据各数量之间的关系，正确列出一元一次不等式．
 24.【答案】 
解：由知，一次函数，反比例函数，
设，则，
，
，
，
即 ，
，
，，
经检验：，是原方程的解，
，
，
；
的坐标为． 【解析】解：把点分别代入和中，得，，，
解得：，，
故答案为，；
见答案；
由平移可知：，
直线的解析式为，
由，解得或舍弃，
，
通过向右平移个单位，向上平移个单位得到，
又由知，，
把点向右平移个单位，向上平移个单位得到．

通过待定系数法即可求出和的值．
设，则，根据四边形的面积构建方程即可解决问题；
根据一次函数，利用方程组求出点的坐标，即可解决问题；
本题考查反比例函数的应用、一次函数的应用，解题的关键是熟练掌握待定系数法，学会构建方程解决问题，学会构建一次函数，利用方程组确定交点坐标，属于中考常考题型．
 25.【答案】 【情境再现】
证明：由阅读材料知≌，
，，，
，即，
，
，即，
在和中，

≌，
；
【迁移应用】
解：猜想：；证明如下：
由【情境再现】知：≌，
，
，
，
，
，
，
，
；
【拓展延伸】
解：猜想：，证明如下：
设交于点，交于点，如图：

由已知得：，是含角的直角三角形，，
，
，，，
∽，
，，
，，，即，
，
，
，
∽，
，
．  【解析】【分析】
【情境再现】由≌，得，，，可证明≌，得；
【迁移应用】由≌，得，可得，从而，，故DG；
【拓展延伸】设交于点，交于点，由已知可得，，，即可得∽，有，，又，可得，故∽，即可得，．
【解答】
【情境再现】
证明：由阅读材料知≌，
，，，
，即，
，
，即，
在和中，

≌，
；
【迁移应用】
解：猜想：；证明如下：
由【情境再现】知：≌，
，
，
，
，
，
，
，
；
【拓展延伸】
解：猜想：，证明如下：
设交于点，交于点，如图：

由已知得：，是含角的直角三角形，，
，
，，，
∽，
，，
，，，即，
，
，
，
∽，
，
．
【点评】
本题考查三角形的综合应用，解题的关键是掌握全等三角形的判定与性质，相似三角形的判定与性质的应用．  26.【答案】解：抛物线交轴于，两点，
，解得：，
该抛物线的解析式为；
在中，令，得，
，
的周长为：，是定值，
当最小时，的周长最小．
如图，点、关于对称轴对称，连接交对称轴于点，则点为所求的点．
，
周长的最小值是：．
，，，
，．
周长的最小值是：．
抛物线对称轴为直线，
设直线的解析式为，
将，代入，得：
，解得：，
直线的解析式为，
；
存在．设，
以为边时，如图，















四边形是菱形，
，
，
解得：，
，，
，，
以为对角线时，如图，














四边形是菱形，
，
，
解得：，
，，
当以为对角线时，则，如图，


解得：，
，，
，，
综上所述，符合条件的点的坐标为：，，，， 【解析】本题是二次函数压轴题，考查了二次函数的图象与性质、待定系数法、图形面积计算、轴对称最短路线，菱形性质，点和线段的平移等知识点，熟练掌握二次函数图象和性质，轴对称性质等相关知识是解题关键．
运用待定系数法即可求得答案；
因为为定值，所以当最小时，的周长最小，如图，连接交对称轴于点，由轴对称性质可知，此点即为所求，再利用勾股定理求出、，即可得出答案；
分三种情况进行讨论：以为边时，由四边形是菱形，可得，建立方程求解即可，以为对角线时．由四边形是菱形，可得，当以为对角线时，则，建立方程求解即可．