2022年贵州省遵义市汇仁中学中考数学一模试题（含答案）

2022年贵州省遵义市汇仁中学中考数学一模试题

一、选择题（本大题共26小题，共78.0分）

1. 已知点，，，，，，其中在坐标轴上的点有

A. 1个 B. 2个 C. 3个 D. 4个

2. 若等式成立，则内的运算符号为

A.  B.  C.  D.

3. 若方程组的解也是方程的解，则k的值为

A. 5 B. 4 C. 3 D. 2

4. 如图，在矩形ABCD中，，，动点M自点A出发沿的方向，以每秒1cm的速度运动，同时动点N自点A出发沿的方向以每秒2cm的速度运动，当点N到达点C时，两点同时停止运动，设运动时间为秒，的面积为，则下列图象中能反映y与x之间的函数关系的是

A.  B.

C.  D.

5. 下列算式中正确的是

A.  B.

C.  D.

6. 下列计算错误的是

A.  B.

C.  D.

7. 如图，向一个半径为R、容积为V的球形容器内注水，则能反映容积内水的体积y与容器内水深x之间的关系的图象可能为

A.

B.

C.

D.

8. 下列运算正确的是

A.  B.

C.  D.

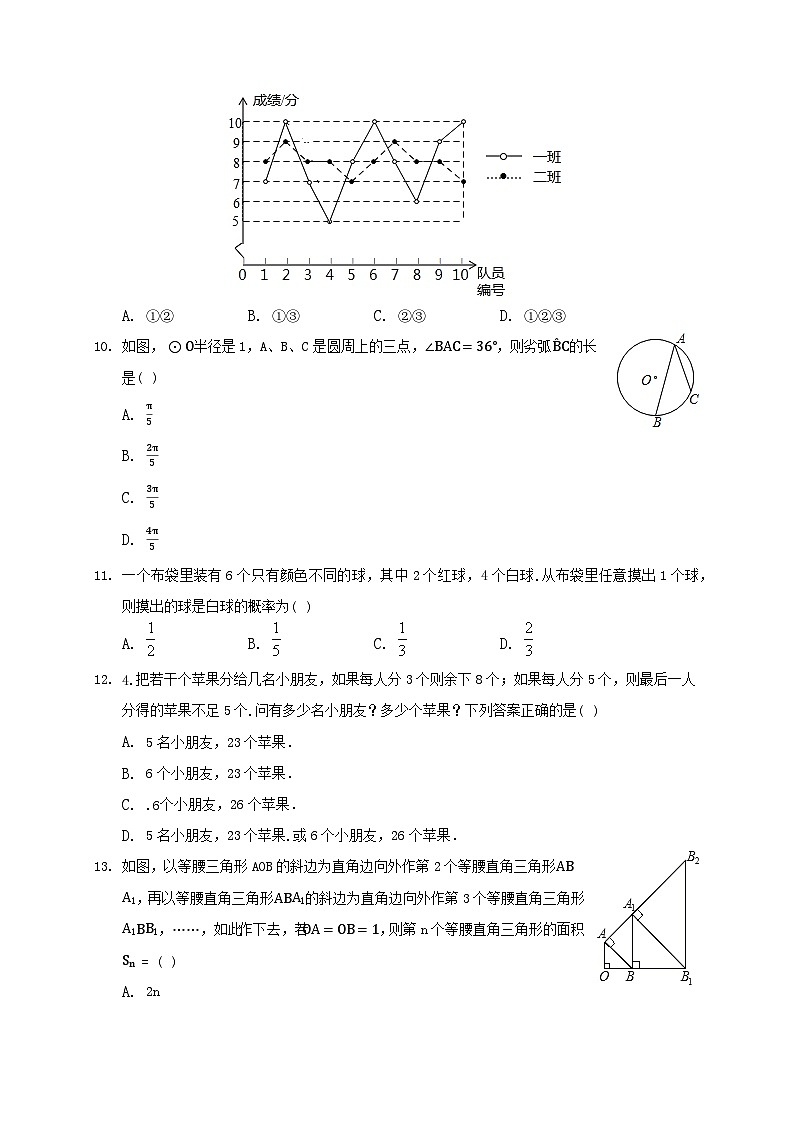
9. 体育节中，某学校组织九年级学生举行定点投篮比赛，要求每班选派10名队员参加．下面是一班和二班参赛队员定点投篮比赛成绩的折线统计图每人投篮10次，每投中1次记1分，请根据图中信息判断：

二班学生比一班学生的成绩稳定；

两班学生成绩的中位数相同；

两班学生成绩的众数相同．

上述说法中，正确的序号是

A.  B.  C.  D.

10. 如图，半径是1，A、B、C是圆周上的三点，，则劣弧的长是

A.

B.

C.

D.

11. 一个布袋里装有6个只有颜色不同的球，其中2个红球，4个白球从布袋里任意摸出1个球，则摸出的球是白球的概率为

A.  B.  C.  D.

12. 把若干个苹果分给几名小朋友，如果每人分3个则余下8个；如果每人分5个，则最后一人分得的苹果不足5个问有多少名小朋友？多少个苹果？下列答案正确的是

A. 5名小朋友，23个苹果．

B. 6个小朋友，23个苹果．

C. 个小朋友，26个苹果．

D. 5名小朋友，23个苹果或6个小朋友，26个苹果．

13. 如图，以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形，再以等腰直角三角形的斜边为直角边向外作第3个等腰直角三角形，，如此作下去，若，则第n个等腰直角三角形的面积

A. 2n

B.

C.

D.

14. 已知a、b互为相反数，则下列结论：；；表示一个数，b一定是负数；设a为一个正数，则a、b在数轴上对应的点关于原点对称，一定正确的结论的个数有

A. 1 B. 2 C. 3 D. 4

15. 如图，≌，则下列结论正确的是

A.  B.  C.  D.

16. 703班有男女同学若干人，女同学因故走了8名，这时男女同学之比为5：2，后来男同学又走了12名，这时男女同学人数相同，那么最初的女同学有

A. 15名 B. 16名 C. 17名 D. 18名

17. 下列说法正确的是

A. 经过三点可以作一个圆 B. 平分弦的直径垂直于这条弦

C. 等弧所对的圆心角相等 D. 三角形的外心到三边的距离相等

18. 在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为完美点．已知二次函数的图象上有且只有一个完美点，且当时，函数的最小值为，最大值为1，则m的取值范围是

A.  B.  C.  D.

19. 下列植物叶子的图案中既是轴对称，又是中心对称图形的是

A.  B.  C.  D.

20. 商店里有A、B、C三种商品，单价分别为50元，30元，10元．若小明购买了两种商品，共花费140元，则小明的购买方案有种．

A. 3 B. 7 C. 10 D. 12

21. 如图，某同学探究n边形的内角和公式，首先将以顶点为端点的对角线、、、、、连接，将此n边形分割成个三角形，然后由每个三角形的内角和为，可得n边形的内角和为该同学的上述探究方法所体现的数学思想是

A. 分类讨论 B. 公理化 C. 类比 D. 转化

22. 下列有理数中，负数的个数是

，，，，

A. 1个 B. 2个 C. 3个 D. 4个

23. 在菱形ABCD中，AC、BD为对角线，若，，则菱形ABCD的面积是

A. 12 B. 16 C. 24 D. 32

24. 小明用计算器计算的值，其按键顺序和计算器显示结果如表：

这时他才明白计算器是先做乘法再做加法的，于是他依次按键：

从而得到了正确结果，已知a是b的3倍，则正确的结果是

A. 24 B. 39 C. 48 D. 96

25. 如图，在中，，AB的垂直平分线交BC于E，交AB于D，连接AE，若AE平分，，则CE的长为

A. 8

B. 6

C. 4

D. 2

26. 如图，中，，BD，CD分别是，的平分线，则的度数是 

A.

B.

C.

D.

二、解答题（本大题共2小题，共16.0分）

27. 按图中程序进行计算：

规定：程序运行到“结果是否大于10”为一次运算．

若运算进行一次就停止，求出x的取值范围；

若运算进行二次才停止，求出x的取值范围．

28. 已知如图：中，，、的平分线相交于点O，过点O作分别交AB、AC于E、F．

写出线段EF与BE、CF间的数量关系？不证明

若，其他条件不变，如图，图中线段EF与BE、CF间是否存在中数量关系？请说明理由．

若中，，的平分线与三角形外角的平分线CO交于O，过O点作交AB于E，交AC于F，如图，这时图中线段EF与BE，CF间存在什么数量关系？请说明理由．

【答案与解析】

1.答案：D

解析：试题分析：从题干中找到横坐标为0，或者纵坐标为0的点，计算个数即可．

在坐标轴上的点有，，，共4个点，故选D．

2.答案：D

3.答案：B

解析：解：，

得：，解得，

把代入得：，解得，

方程组的解为，

把代入方程得：，

解得．

故选：B．

解关于x，y的方程组，求得x，y的值，再代入，求得k的值．

此题主要考查了二元一次方程组的解，先通过解二元一次方程组，求得解后再代入关于k的方程即可求解．

4.答案：D

解析：解：在矩形ABCD中，，，

，

点M以每秒1cm的速度运动，

秒，

点N以每秒2cm的速度运动，

秒，

点N先到达终点，运动时间为3秒，

点N在AD上运动时，；

点N在DC上运动时，，

能反映y与x之间的函数关系的是D选项．

故选：D．

以AM为底边，分点N在AD上运动与在DC上运动两段，根据三角形的面积公式分别求出运动时的y与x之间的函数关系，然后根据二次函数图象与一次函数图象观察各选项中的图象即可得解．

本题考查了动点问题的函数图象，二次函数图象，三角形的面积，矩形的性质，根据题意理清动点的时间分段，并根据三角形的面积公式列出函数关系式是解题的关键，难度不大．

5.答案：B

解析：解：A、t与不是同类项，不能合并，故本选项错误；

B、--，故本选项正确；

C、应为，故本选项错误；

D、应为，故本选项错误．

故选：B．

根据同底数幂相除，底数不变指数相减；合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变；单项式与多项式相乘，先用单项式乘多项式的每一项，再把所得的积相加，对各选项分析判断后利用排除法求解．

本题主要考查合并同类项，同底数幂的除法，单项式与多项式相乘，熟练掌握运算性质是解题的关键．

6.答案：A

解析：

本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．根据二次根式的加减法对A、C进行判断；根据二次根式的除法法则对C进行判断；根据二次根式的乘法法则对D进行判断．

解：原式，所以A选项的计算错误；

B.原式，所以B选项的计算正确；

C.原式，所以C选项的计算正确；

D.原式，所以D选项的计算正确．

故选A．

7.答案：A

解析：解：根据球形容器形状可知，函数y的变化趋势呈现出，当时，y增量越来越大，当时，y增量越来越小，

曲线上的点的切线斜率先是逐渐变大，后又逐渐变小，故y关于x的函数图象是先凹后凸．

故选：A．

水深h越大，水的体积v就越大，故容器内水的体积y与容器内水深x间的函数是增函数，根据球的特征进行判断分析即可．

本题主要考查了函数图象的变化特征，解题的关键是利用数形结合的数学思想方法．解得此类试题时注意，如果水的体积随深度的增加而逐渐变快，对应图象是曲线从缓逐渐变陡．

8.答案：D

解析：解：A、，错误；

B、，错误；

C、，错误；

D、，正确；

故选：D．

根据完全平方公式和平方差公式解答即可．

此题考查平方差公式，关键是根据完全平方公式和平方差公式解答．

9.答案：A

解析：解：一班10名队员投篮成绩：7，10，7，5，8，10，8，6，9，10；

从小到大排列为：5，6，7，7，8，8，9，10，10，10，中位数为：8；众数为：10；平均数为8；方差为；

二班10名队员投篮成绩：8，9，8，8，7，8，9，8，8，7；

从小到大排列为：7，7，8，8，8，8，8，8，9，9，则中位数为：8；，众数为：8；平均数为：8；方差为

正确，错误，

二班的方差小于一班的方差，

二班学生比一班学生的成绩稳定，

正确，

故选：A．

求出两个班的众数，中位数，方差即可判断．

本题考查折线统计图，中位数，众数，方差等知识，解题的关键是熟练掌握基本计算公式，属于中考常考题型．

10.答案：B

解析：解：连OB，OC，如图，

，

，

劣弧的长．

故选B．

连OB，OC，根据圆周角定理得到，然后根据弧长公式计算劣弧的长．

本题考查了弧长公式：也考查了圆周角定理．

11.答案：D

解析：本题主要考查随机事件概率的求法计算时找准两点：全部等可能情况的总数；符合条件的情况数目；二者的比值就是其发生的概率个球中，白球有4个，由此可以求出结果．

解：袋中装有6个只有颜色不同的球，其中4个白球， 

从布袋中随机摸出1个球，摸出的球是白球的概率  

故选D．

12.答案：D

解析：分析

此题考查了一元一次不等式组的应用，其中根据题意表示出最后一名小朋友分到的苹果数是解本题的关键．设小朋友为x人，根据每位小朋友分3个苹果，则还剩8个苹果，表示出苹果的个数，再由每位小朋友分5个苹果，根据人数为x人，表示出需要苹果的个数，减去苹果的总数，即为最后一名小朋友分到的苹果数，再利用“最后一位小朋友分到了苹果，但不足5个，但至少有1个”列出关于x的不等式，求出不等式的解集，在解集中找出正整数解得到x的值，即为小朋友的人数，即可得到苹果的个数．

解答

解：设有x名小朋友，则有个苹果根据题意，得

解得：

因为x为整数，所以或当时，当时，

故选D．

13.答案：B

解析：

本题考查了等腰直角三角形的性质，数字变化规律的考查，根据等腰直角三角形的斜边等于直角边的倍，表示出后一个三角形的直角边与前一个三角形的直角边的关系，然后得到相邻两个三角形的面积的关系是解题的关键．

根据等腰直角三角形的斜边等于直角边的倍表示出下一个三角形的直角边，然后分别求出各个三角形的面积，不难发现，后一个三角形的面积是前一个三角形面积的2倍，然后找出规律写出第n个三角形的面积的表达式．

解：根据等腰直角三角形的性质，，，，

所以，第1个等腰直角的面积，

第2个等腰直角的面积，

第3个等腰直角的面积，

第4个等腰直角的面积，

，

依此类推，第n个等腰直角三角形的面积．

故选B．

14.答案：C

解析：解：若a、b互为相反数，

则：；正确；

；正确；

表示一个数，b不一定是负数；错误；

设a为一个正数，则a、b在数轴上对应的点关于原点对称，正确；

故选：C．

根据相反数的定义：只有符号不同的两个数叫做互为相反数，结合数轴进行判断即可．

此题主要考查了相反数和数轴，关键是掌握相反数的定义．

15.答案：D

解析：

根据全等三角形的对应边相等、对应角相等判断即可．

本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键．

解：≌，

，A错误；

≌，

，B错误；

，即，C错误、D正确；

故选：D．  

16.答案：B

解析：解：设最初的女同学有x人，最初的男同学有y人，

依题意，得：，

解得：．

故选：B．

设最初的女同学有x人，最初的男同学有y人，根据“女同学因故走了8名，这时男女同学之比为5：2，后来男同学又走了12名，这时男女同学人数相同”，即可得出关于x，y的二元一次方程组，解之即可得出结论．

本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．

17.答案：C

解析：解：A、经过不共线的三点可以作一个圆，所以A选项的说法错误；

B、平分弦非直径的直径垂直于这条弦，所以B选项的说法错误；

C、等弧所对的圆心角相等，所以C选项的说法正确；

D、三角形的外心到三个顶点的距离相等，所以D选项的说法错误；

故选：C．

利用确定圆的条件对A进行判断；利用垂径定理对B进行判断；根据圆心角、弧、弦的关系对C进行判断；根据三角形外心的性质对D进行判断．

本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．也考查了确定圆的条件和垂径定理．

18.答案：C

解析：解：令，即，

由题意，，即，

又方程的根为，

解得，，

故函数，

如图，该函数图象顶点为，与y轴交点为，由对称性，该函数图象也经过点．

由于函数图象在对称轴左侧y随x的增大而增大，在对称轴右侧y随x的增大而减小，且当时，函数的最小值为，最大值为1，

，

故选：C．

根据和谐点的概念令，即，由题意，，即，方程的根为，从而求得，，所以函数，根据函数解析式求得顶点坐标与纵坐标的交点坐标，根据y的取值，即可确定x的取值范围．

本题是二次函数的综合题，考查了二次函数图象上点的坐标特征，二次函数的性质以及根的判别式等知识，利用分类讨论以及数形结合得出是解题关键．

19.答案：D

解析：解：A、是轴对称，不是中心对称图形，故本选项错误；

B、是轴对称，不是中心对称图形，故本选项错误；

C、不是轴对称，也不是中心对称图形，故本选项错误；

D、既是轴对称又是中心对称图形，故本选项正确．

故选：D．

根据中心对称图形和轴对称图形的概念对各选项分析判断即可得解．

本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

20.答案：B

解析：解：设A种商品买x件，B种商品买y件，

由题意得：

、y都是正整数

，

设A种商品买a件，C种商品买b件；

由题意得：

、b都是正整数

，．

设B种商品买m件，C种商品买n件，

由题意得：

、n都是正整数

，，，．

综合以上可得小明的购买方案有7种．

故选：B．

需要分类讨论：设A种商品买x件，B种商品买y件；设A种商品买a件，C种商品买b件；设B种商品买m件，C种商品买n件．列出方程并解答．

本题考查了二元一次方程的应用．解题的难点是挖掘题目中的关系，找出等量关系，列出二元一次方程．然后根据未知数的实际意义求其整数解．

21.答案：D

解析：解：探究多边形内角和公式时，从n边形的一个顶点出发引出条对角线，将n边形分割成个三角形，这个三角形的所有内角之和即为n边形的内角和，这一探究过程运用的数学思想是转化思想，

故选D．

根据题意即可得到结论．

本题考查了多边形的内角和公式，数学思想，熟练掌握数学思想是解题的关键．

22.答案：C

解析：

本题考查的是正数和负数、绝对值、有理数的乘方，掌握相关的概念和性质是解题的关键．

根据去括号法则、有理数的乘方法则、绝对值的性质进行计算，判断即可．

解：，是正数，，是负数；，是负数，，是正数；，是负数；

故选：C．

23.答案：B

解析：

本题考查了菱形的性质，熟练运用菱形的性质是本题的关键．

根据菱形面积、b是两条对角线的长度，可求菱形ABCD的面积．

解：菱形ABCD的面积

菱形ABCD的面积

故选：B．  

24.答案：C

解析：解：由题意可得：，

则，

解得：，

故．

故选：C．

根据题意得出关于a，b，c的方程组，进而解出a，b，c的值，进而得出答案．

此题主要考查了计算器的应用以及方程组的解法，正确得出关于a，b，c的等式是解题关键．

25.答案：D

解析：【试题解析】

解：是线段AB的垂直平分线，，

，

平分，

，

即，

．

平分，，

，

，，

，

，

，

故选：D．

先由线段垂直平分线的性质及求出，再由AE平分可得出，由三角形内角和定理即可求出的度数，然后根据角平分线上的点到角的两边距离相等可得，根据直角三角形角所对的直角边等于斜边的一半可得，进而得出CE即可．

本题考查了角平分线上的点到角的两边距离相等的性质，直角三角形角所对的直角边等于斜边的一半的性质，熟记各性质并准确识图是解题的关键．

26.答案：C

解析：

本题考查的是三角形内角和定理，熟知三角形内角和是是解答此题的关键．

先根据三角形内角和定理求出的度数，再由角平分线的性质求出的度数，进而可得出结论．

解：中，，

．

，CD分别是，的平分线，

，

．

故选C．

27.答案：解：根据题意可得：，

，

根据题意可得：

解得：

解析：根据运行程序，第一次运算结果大于10，列出不等式可求解；

根据运行程序，第一次运算结果小于或等于10，第二次运算结果大于10列出不等式组，然后求解即可．

本题考查了一元一次不等式及一元一次不等式组的应用，读懂题目信息，理解运行程序并列出不等式组是解题的关键．

28.答案：解：

；

仍然有理由如下：

，

，

平分，

，

，

，同理，

；

理由如下：

，

，

平分，

，

，

，

同理可得到，

．

解析：根据平行线和角平分线容易得到，，可得到结论；

仍然存在，可利用角平分线的定义和平行线的性质得到，，可得出；

同样的方法可证得，，可得到．

本题主要考查等腰三角形的判定及平行线的性质，根据条件证得、是解题的关键．