2023年山东省邹城市第六中学南校区中考数学模拟试卷（含答案）

这是一份2023年山东省邹城市第六中学南校区中考数学模拟试卷（含答案），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年山东省邹城市第六中学南校区中考数学模拟试卷 一、选择题（本大题共10小题，共30.0分）1. 我们对正数2022进行开平方，再对得到的算术平方根进行开平方，，如此进行下去，会发现所得的算术平方根越来越接近A. 0 B. 1 C.  D. 20222. 南平市是福建省九地市区域面积最大的地级市，它的面积约为26300平方千米，占全省的区域面积的以上．将26300用科学记数法表示为平方千米．A.  B.  C.  D. 3. 有四张质地相同的卡片，它们的背面相同，其中两张的正面印有“粽子”的图标，另外两张的正面印有“龙舟”的图案，现将它们背面朝上，洗均匀后排列在桌面，任意翻开两张，那么两张图案一样的概率是A.  B.  C.  D. 4. 下列运算一定正确的是A.  B.  C.  D. 5. 下列各式的最小值是A.  B.  C.  D. 6. 在下列四个图形中，是三棱锥的平面展开图形的为A.  B.  C.  D. 7. 如图，有一圆通过的三个顶点，且弦BC的中垂线与相交于D点．若，，则的度数为何？A. 23B. 28C. 30D. 378. 在，，，，，中，无理数的个数是A. 1个 B. 2个 C. 3个 D. 4个9. 要使是完全平方式，则m的值为   A.  B. 2 C.  D. 10. 下列关于抛物线的说法不正确的是A. 抛物线开口向上 B. 抛物线的顶点是C. 抛物线与y轴的交点是 D. 当时，y随x的增大而增大二、填空题（本大题共7小题，共28.0分）11. 已知二元一次方程组，则得                  12. 将抛物线绕顶点旋转后的图象的解析式为______．13. 若扇形的面积为，半径等于3，则它的圆心角等于______．14. 关于x的一元二次方程有两个相等的实数根，则代数式的值是______ ．15. 如果，那么代数式的值是______．16. 如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，，若的面积为1，则平行四边形ABCD的面积为___．  17. 如图，在中，，D、E、F分别为AC、BC、AB的中点，若，，则与的周长的和为______ ．
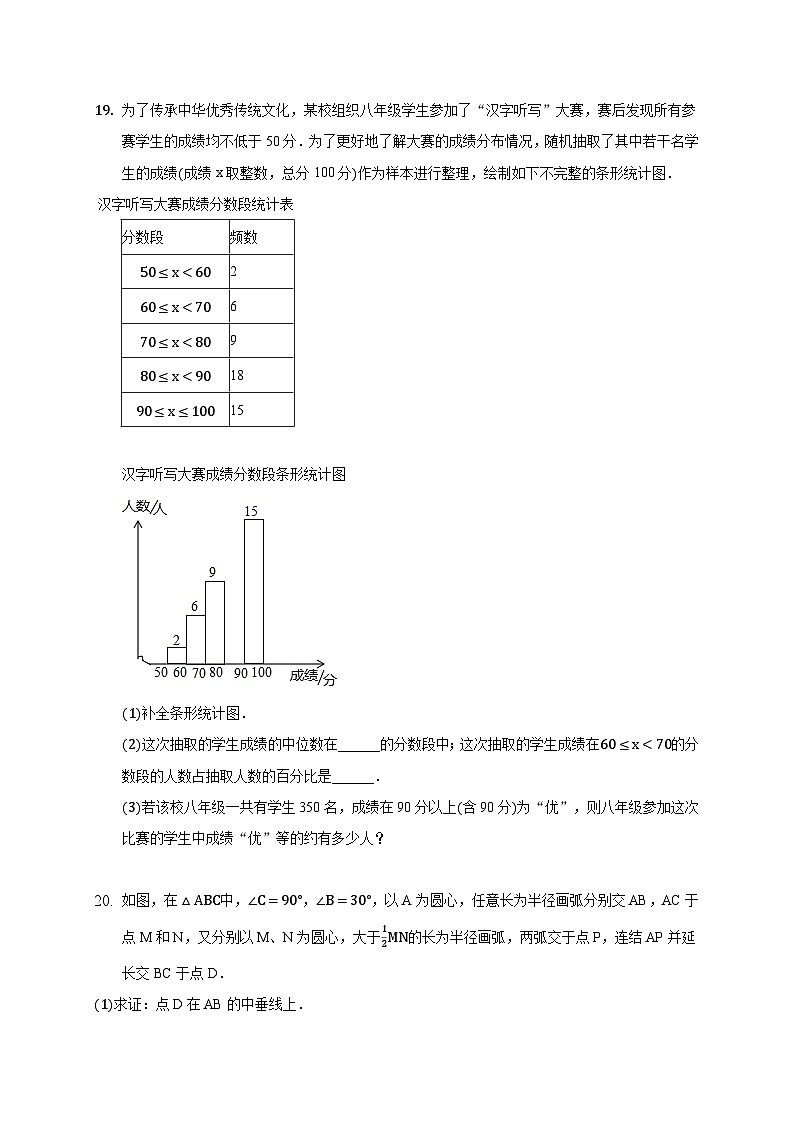
三、解答题（本大题共8小题，共62.0分）18. 求不等式组的非负整数解． 19. 为了传承中华优秀传统文化，某校组织八年级学生参加了“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解大赛的成绩分布情况，随机抽取了其中若干名学生的成绩成绩x取整数，总分100分作为样本进行整理，绘制如下不完整的条形统计图． 汉字听写大赛成绩分数段统计表   分数段频数2691815 汉字听写大赛成绩分数段条形统计图 补全条形统计图．这次抽取的学生成绩的中位数在______的分数段中；这次抽取的学生成绩在的分数段的人数占抽取人数的百分比是______．若该校八年级一共有学生350名，成绩在90分以上含90分为“优”，则八年级参加这次比赛的学生中成绩“优”等的约有多少人？ 20. 如图，在中，，，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，又分别以M、N为圆心，大于的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D．求证：点D在AB的中垂线上．当时，求的面积．
 21. 如图，在平面直角坐标系xOy中，直线与函数的图象交于A，B两点，且点A的坐标为．求k的值；已知点，过点P作平行于y轴的直线，交直线于点C，交函数的图象于点D．当时，求线段CD的长；若，结合函数的图象，直接写出m的取值范围．
 22. 某县坚持民生工程优先，积极治理内河水质，为了解决生活污水排放问题，需要铺设一段全长为420m的污水排放管道铺设120m后，为了尽量减少施工对城市交通所造成的影响，后来每天的工效比原计划增加，结果共用32天完成这一任务求原计划每天铺设管道的长度为多少米？ 23. 如图，正方形ABCD的边CD在正方形ECGF的边CE上，B、C、G三点在一条直线上，且边长分别为2和3，在BG上截取，连接AP、PF． 观察猜想AP与PF之间的大小关系，并说明理由；图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由；若把这个图形沿着PA、PF剪成三块，请你把它们拼成一个大正方形，在原图上画出示意图，并请求出这个大正方形的面积． 24. 如图，在中，，，，点P在AB上，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也运动到点B时停止．在点E、F运动过程中，以EF为直径作圆．设点E运动的时间为t秒．当以EF为直径的圆与的边相切时，求t的值；当时，写出以EF为直径的圆与的重叠部分的面积S与t的函数表达式．
 25. 如图，直线与x轴交于点C，与y轴交于点B，经过B、C两点的抛物线与x轴的另一个交点为A．求抛物线的解析式；点E是直线BC上方抛物线上的一个动点，过点E作y轴的平行线交直线BC于点M，当面积最大时，求出点M的坐标；在的结论下，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P，Q，A，M为顶点的四边形是平行四边形？如果存在，请求出点P的坐标：如果不存在，请说明理由．
 
【答案与解析】1.答案：B解析：解：对2016开平方，再对得到的算术平方根进行开平方，n次以后得到由于当n无限大时，接近0．由于所以对正数2016进行开平方，再对得到的算术平方根进行开平方，，如此进行下去，其结果越来越接近1．故选：B．任何正数的算术平方根无限次的开平方，最后的结果都接近1本题考查了算术平方根的定义和性质．2.答案：B解析：解：，故选：B．科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．3.答案：A解析：解：列树状图得： 共有12种情况，两张图案一样的有4种情况，所以概率是，故选A．列举出所有情况，看所求的情况占总情况的多少即可．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率注意本题是不放回实验．4.答案：A解析：解：A、，故本选项符合题意；B、，故本选项不符合题意；C、，故本选项不符合题意；D、，故本选项不符合题意；故选：A．分别根据幂的乘方运算法则，积的乘方运算法则，同底数幂的乘法法则以及同底数幂的除法法则逐一判断即可．本题考查了同底数幂的乘除法以及幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键．5.答案：A解析：解：，，，，是最小的，故选：A．分别计算每一个选项，进行比较大小即可．本题考查有理数的概念；熟练掌握有理数的绝对值、相反数的性质是解题的关键．6.答案：B解析：解：A、此图形可以围成三棱柱，故此选项错误；B、此图形可以围成三棱锥，故此选项正确；C、此图形可以围成四棱锥，故此选项错误；D、无法围成立体图形，故此选项错误．故选：B．根据三棱锥的四个面都是三角形，还要能围成一个立体图形，进而分析得出即可．本题主要考查了图形展开的知识点，注意几何体的形状特点进而分析才行．7.答案：B解析：解：有一圆通过的三个顶点，且的中垂线与相交于D点，，，．故选：B．由有一圆通过的三个顶点，且的中垂线与相交于D点．若，，可求得与的度数，继而求得答案．此题考查了圆周角定理以及弧与圆心角的关系．此题难度不大，注意掌握数形结合思想的应用．8.答案：C解析：试题分析：无理数包括三方面的数：含的，一些开方开不尽的根式，一些有规律的数，根据以上内容判断即可．无理数有，，，共3个，．故选C．9.答案：D解析：解：因为是完全平方式，所以可得：，所以，故应选D．10.答案：C解析：解：A，由抛物线可看出，故开口向上，故说法正确．B，因为顶点坐标是，故说法正确；C，当时，，故与与y轴交点为，故说法不正确D，由于开口方向向上，对称轴为，时y随x的增大而增大，故说法正确；故选：C．根据抛物线的解析式得出顶点坐标是，对称轴是直线，根据，得出开口向上，当时，y随x的增大而增大，把代入求得，根据结论即可判断选项．本题主要考查对二次函数的性质的理解和掌握，能熟练地运用二次函数的性质进行判断是解此题的关键．11.答案：解析：本题考查二元一次方程组解法中的加减消元法。解：得12.答案：解析：解：，，，抛物线的顶点坐标为，抛物线绕顶点旋转后的图象的解析式为，即．故答案为：．先将函数解析式整理成顶点式形式并求出顶点坐标，再根据绕顶点旋转后的图象与原图象开口相反，利用顶点式解析式写出即可．本题考查了二次函数图象与几何变换，平移的规律：左加右减，上加下减，此类题目，利用顶点的变化求解更简便．13.答案：解析：本题考查了扇形的面积计算，属于基础题，解答本题的关键是掌握扇形的面积计算公式，及公式里面字母所代表的含义．根据扇形的面积公式，然后代入面积及半径，即可得出n的值．解：由题意得，扇形的面积为3，半径，即可得：，解得：．故答案为．  14.答案：解析：解：根据题意得且，即，，所以原式，故答案为．先根据一元二次方程的定义以及根的判别式得到且，则，再将代数式变形后把代入计算即可．本题考查了一元二次方程的根的判别式：当，方程有两个不相等的实数根；当，方程有两个相等的实数根；当，方程没有实数根．也考查了一元二次方程的定义．15.答案：5解析：解：原式，当时，原式，故答案为：5原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把代入计算即可求出值．此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．16.答案：12解析：此题考查了相似三角形的判定与性质与平行四边形的性质．此题难度适中，注意数形结合思想的应用，注意相似三角形面积的比等于相似比的平方定理的应用由四边形ABCD是平行四边形，根据平行四边形对边平行且相等，即可得，，，然后由平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，即可判定∽，∽，又由相似三角形面积的比等于相似比的平方，即可求得答案．解：，，∽，∽，，，，的面积为，的面积为，平行四边形ABCD面积为．故答案为：  17.答案：30解析：解：，，，，、E、F分别为AC、BC、AB的中点，，，与的周长的和的周长．故答案为：30．利用勾股定理列式求出AC，再根据三角形的中位线平行于第三边并且等于第三边的一半可得，，然后求出与的周长的和等于的周长，代入数据计算即可得解．本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理，熟记定理并求出两三角形的周长之和等于的周长是解题的关键．18.答案：解：解不等式，得，解不等式，得，不等式组的解集为：，不等式组的非负整数解为：0，1．解析：先求出每个不等式的解集，再求出不等式组的解集，最后求出答案即可．本题考查了解一元一次不等式组和不等式组的整数解，能求出不等式组的解集是解此题的关键．19.答案：解补全条形图如下：被调查的总人数为人，而第25、26个数据均落在，这次抽取的学生成绩的中位数在的分数段中，这次抽取的学生成绩在的分数段的人数占抽取人数的百分比是，故答案为：，；．答：该年级参加这次比赛的学生中成绩“优”等的约有105人．解析：根据频数分布表补全条形图即可得；根据中位数的定义求解可得，将成绩在的分数段的人数除以总人数可得百分比；用总人数乘以样本中90分以上含90分的人数所占比例可得．本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．20.答案：解：证明：根据作图过程可知：AD是平分线，，，所以点D在AB中垂线上；当时，，，，所以．解析：根据作图过程可得，AD是平分线，再根据，，可得，进而可证明点D在AB的中垂线上；根据含30度角的直角三角形可得AC和BC的长，进而可得的面积．本题考查了作图基本作图、线段垂直平分线的性质、含30度角的直角三角形，解决本题的关键是掌握基本作图．21.答案：解：点在直线上，，点A的坐标为，代入函数中，得．当时，．直线，反比例函数的解析式为．，，．如图，解得或，，由图象可得：当，或时，．解析：将点A坐标代入直线解析式可求a的值，再将点A坐标代入反比例函数解析式可求k的值；求出点C，点D两点坐标，即可求CD的长；根据图象可解．本题考查了一次函数与反比例函数的交点问题，待定系数法求解析式，利用函数图象性质解决问题是本题的关键．22.答案：解：设原计划每天铺设管道的长度为x米，则提高工作效率后每天铺设管道的长度为米，依题意得：，解得：，经检验，是原方程的解，且符合题意．答：原计划每天铺设管道的长度为10米．解析：设原计划每天铺设管道的长度为x米，则提高工作效率后每天铺设管道的长度为米，根据工作时间工作总量工作效率，结合共用32天完成这一任务．即可得出关于x的分式方程，解之经检验后即可得出结论．本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．23.答案： 解：猜想；理由：正方形ABCD、正方形ECGF，，，，，，，≌，．存在，是和，变换过程：把先向右平移5个单位，使AB在GF边上，B与G重合，再绕G点逆时针旋转90度，就可与重合．答案不唯一 如图：．解析：证AP与PF所在的三角形全等即可；将中的先平移后旋转得到；大正方形的面积是由原来的正方形的面积分割而成的，所以等于．24.答案：解：当时，如图1所示：设与AC相切，切点为H，连接PH，则，，，即；当时，如图2所示：设EF的中点为Q，若与BC相切，切点为M，连接QM，则．，，．由题意知，的半径为2，即．，，，；当时，如图3所示：设EF的中点为R，若与AC相切，切点为N，连接RN，则，此时；，，∽，，，解得：，，；综上所述：t的值为1或或4；如图4所示：设与BC的交点为D，连接RD，若的半径为r，则，，，为等边三角形，的面积，又扇形RED的面积，．解析：分三种情况：当时，由含的直角三角形的性质容易得出t的值；当时，设EF的中点为Q，若与BC相切，切点为M，连接QM，则先求出QM，再求出QB、AQ、AE，即可得出t的值；当时，设EF的中点为R，若与AC相切，切点为N，连接RN，则，；先证明∽，得出比例式求出半径NR，得出AE，即可求出t的值；设与BC的交点为D，连接RD，若的半径为r，则，先证明为等边三角形，得出的面积，由扇形RED的面积，即可求出S与t的函数关系式．本题是圆的综合题，考查了切线的性质、直角三角形的性质、相似三角形的判定与性质、等边三角形的判定与性质以及面积的计算等知识；本题难度较大，综合性强，特别是中，需要通过作辅助线、分类讨论才能得出结果．25.答案：解：令，则，即点，点，则抛物线，将点C坐标代入上式并解得：，故抛物线的表达式为：；设点，则点，，，故有最大值，此时，故点；设点，点，当AM是平行四边形的一条边时，当点P在对称轴的右侧时，点M向左平移4个单位向下平移个单位得到A，同理向左平移4个单位向下平移个单位得到，即，解得：，故点；当点P在对称轴的左侧时，同理可得点；当AM是平行四边形的对角线时，AM的中点坐标为，此坐标即为PQ的中点坐标，即，解得：，故点；综上，点或或解析：令，则，即点，点，则抛物线，将点C坐标代入上式，即可求解；由，即可求解；分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到平行四边形的性质、图形的平移、面积的计算等，其中，要注意分类求解，避免遗漏．