2023年天津市滨海新区中考数学+仿真+模拟试卷（含答案）

这是一份2023年天津市滨海新区中考数学+仿真+模拟试卷（含答案），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年天津市滨海新区中考数学 仿真 模拟试卷一、选择题（本大题共12小题，共36.0分）1.  计算的结果是(    )A.  B.  C.  D. 2.  已知为锐角且，则(    )A.  B.  C.  D. 不能确定3.  下列图形中，既是轴对称图形，又是中心对称图形的是(    )A.  B.  C.  D. 4.  今年春节档电影中，流浪地球凭借优质的口碑一路逆袭，被很多人评为“国产科幻电影之光”，吸引众多影迷纷纷走入影院为这部国产科幻电影打卡据了解流浪地球上映首日的票房约为元，数字用科学记数法表示为(    )A.  B.  C.  D. 5.  如图是由个相同的小正方体组成的几何体，其主视图是(    )A.
B.
C.
D. 6.  已知，是两个连续整数，，则，分别是(    )A. ， B. ， C. ， D. ，7.  方程组的解为(    )A.  B.  C.  D. 8.  计算的结果为(    )A.  B.  C.  D. 9.  已知点，，在下列某个函数的图象上，则这个函数是(    )A.  B.
C.  D. 10.  我们知道四边形具有不稳定性如图，在平面直角坐标系中，边长为的正方形的边在轴上，的中点是坐标原点，固定点，，把正方形沿箭头方向推，使点落在轴正半轴上点处，则点的对应点的坐标为(    )A.  B.  C.  D. 11.  如图，在中，，将绕点按逆时针方向旋转得到，若点恰好落在边上，且，则旋转角的度数为(    )A.
B.
C.
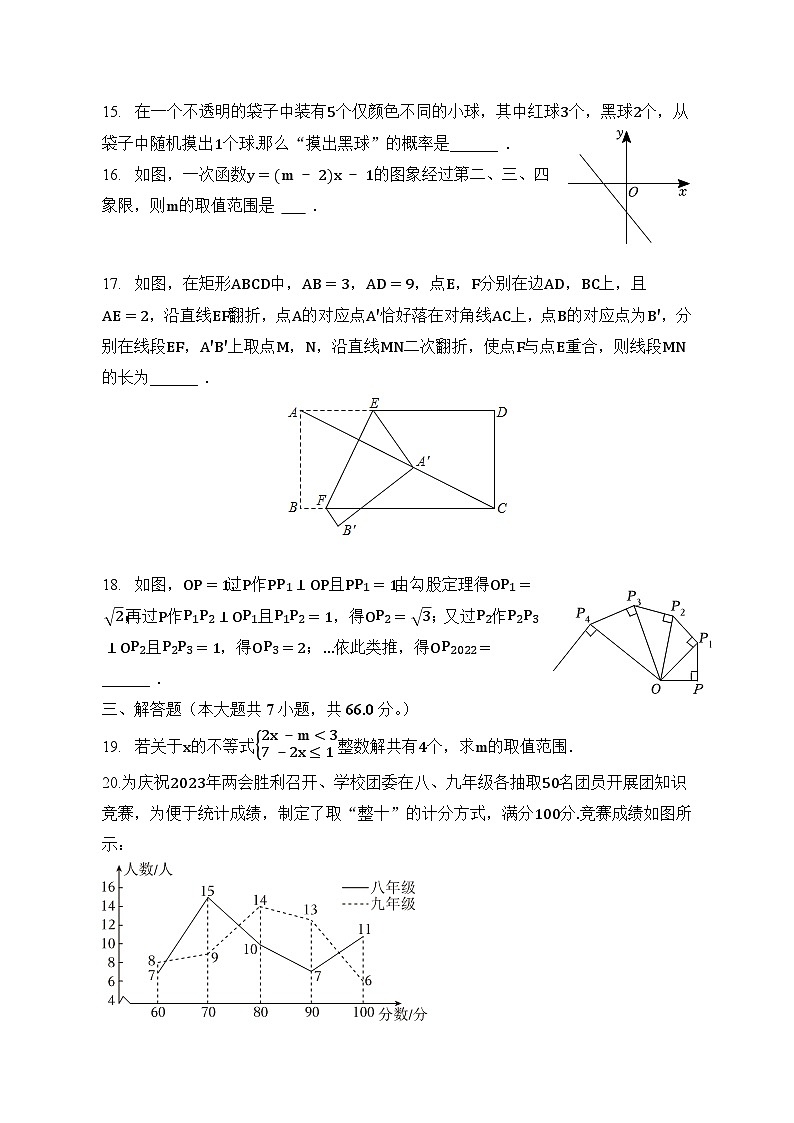
D. 12.  抛物线为常数开口向上，且过点，，下列结论：；若点，都在抛物线上，则；；若方程没有实数根，则，其中正确结论的序号为(    )A.  B.  C.  D. 二、填空题（本大题共6小题，共18.0分）13.  若，则 ______ ．14.  计算： ______ ．15.  在一个不透明的袋子中装有个仅颜色不同的小球，其中红球个，黑球个，从袋子中随机摸出个球那么“摸出黑球”的概率是______ ．16.  如图，一次函数的图象经过第二、三、四象限，则的取值范围是        ．
 17.  如图，在矩形中，，，点，分别在边，上，且，沿直线翻折，点的对应点恰好落在对角线上，点的对应点为，分别在线段，上取点，，沿直线二次翻折，使点与点重合，则线段的长为______ ．
18.  如图，，过作且，由勾股定理得；再过作且，得；又过作且，得；依此类推，得 ______ ．三、解答题（本大题共7小题，共66.0分。）19.  若关于的不等式整数解共有个，求的取值范围．20.为庆祝年两会胜利召开、学校团委在八、九年级各抽取名团员开展团知识竞赛，为便于统计成绩，制定了取“整十”的计分方式，满分分竞赛成绩如图所示：
 众数中位数方差八年级竞赛成绩九年级竞赛成绩你能用成绩的平均数判断哪个年级的成绩比较好吗？通过计算说明理由；
请根据图表中的信息，回答下列问题．
表中 ______ 、 ______ ．
现要给成绩突出的年级领奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级领奖？
若规定成绩分获特等奖，分获一等奖，分获二等奖，直接说出哪个年级的获奖率高？21.如图，是的直径，点是上一点，与过点的切线垂直，垂足为点，直线与的延长线相交于点，弦平分，交于点，连接．
求证：平分；
若，，求线段的长．
22.乒乓球台如图的支架可近似看成圆弧，其示意图如图，与所在的直线过弧所在圆的圆心，直线与弧所在的圆相切于点，连接，，且，．

求证：；
若弓形的高为，，且，求的长．23.如图，一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发，设慢车行驶的时间为，两车之间的距离为，图中的折线表示与之间的函数关系根据图象解决下列问题：
求慢车和快车的速度；
求线段所表示的与之间的函数关系式，并写出自变量的取值范围．
24.【基础巩固】：
如图，四边形中，平分，．
求证：；
【迁移运用】：
如图，在的条件下，取的中点，连结交于点，若，，求的长；

【解决问题】：
如图，四边形中，，，在上取点，使得，恰有若，，求四边形的面积． 25.如图，已知抛物线与轴交于，两点，与轴交于点，点的坐标为．

求抛物线的表达式；
点是抛物线对称轴上的一个动点，求的最小值；
设点是抛物线上一点，其横坐标为，在抛物线上是否存在一点，使得被直线平分？若存在，请求出点的坐标；若不存在，说明理由．
 1.    2.    3.    4.    5. 6.    7.    8.    9.    10. 11.   12. 13.     14.    15. 16.     17.     18. 19.解：解得，
解得，
故原不等式组的解集为．
已知不等式组的的整数解共有个，
则不等式组的整数解为、、、，
，
． 20.解：（1）由题意得：
八年级成绩的平均数是：（60×7+70×15+80×10+90×7+100×11）÷50=80（分），
九年级成绩的平均数是：（60×8+70×9+80×14+90×13+100×6）÷50=80（分），
故用平均数无法判定哪个年级的成绩比较好；
（2）①九年级竞赛成绩中8出现的次数最多，
故众数m=8；
九年级竞赛成绩的方差为：，
所以n=156，
②如果从众数角度看，八年级的众数为7，九年级的众数为8，
所以应该给九年级颁奖；
如果从方差角度看，八年级的方差为188，九年级的方差为156，
又因为两个年级的平均数相同，九年级的成绩的波动小，
所以应该给九年级颁奖，
综上所述，应该给九年级颁奖；
（3）九年级的获奖率高，
八年级的获奖率为：（10+7+11）÷50=56%，
九年级的获奖率为：（14+13+6）÷50=66%，
∵66%＞56%，
∴九年级的获奖率高．21.证明：如图，

为的切线，
，
，
，
，
，
，
，
平分；
解：连接，如图，

是的直径，
，，
平分，
，
，
为等腰直角三角形，
，
，，
∽，
，
，
，
． 22.证明：如图，延长，交于点，则点是弧所在圆的圆心，连接，
直线与圆相切于点，
，，
，，，
≌，
，，
，，
，
，，
；
解：如图，连接，设与交于点，
，，，
，
，
，，，
，，弓形高，
，
在中，由勾股定理得：，
．
 23.解：由题意，得
快车与慢车的速度和为：，
慢车的速度为：，
快车的速度为： ．
答：快车的速度为，慢车的速度为；
由题意得，快车走完全程的时间为：，
时时两车之间的距离为：．
则．
设线段的解析式为，由题意，得
，
解得：，
则，自变量的取值范围是． 24.证明：平分，
．
又，，
≌，
；
解：≌，
，．
，
，
，
∽，
．
是的中点，
．
，
；
解：如图，连结，，

，，，
≌，
，
，
，
，
．
，
．
设，由勾股定理得，
即，
解得负值舍去，
，
四边形的面积． 25.解：把点代入中，得，
解得，
故抛物线的表达式为；
由，令，，
点的坐标为．
令，则，
解得，，
点的坐标为，

，．
连接交抛物线对称轴于点，则此时的值最小，
、关于抛物线的对称轴对称，
，
．
在中，，
的最小值为；
点是抛物线上一点，其横坐标为，
，
．
设直线的表达式为，将点、代入可得

．
设点，
线段的中点的坐标为．
直线平分线段，
直线过点，
将点的坐标代入，得，
解得，，
当时，；
当时，，
点或