2023年浙江省绍兴市新昌县澄潭中心学校中考数学一模试卷（含答案）

新昌县澄潭中学2023年第一次模拟考试

数学科试卷

一       、选择题（本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）

1.一个正方体沿四条棱的中点切割掉一部分后，如图所示，则该几何体的左视图是（    ）

A．  B．  C． D．

2.植树节当天，七年级1班植树300棵，正好占这批树苗总数的，七年级2班植树棵数是这批树苗总数的，则七年级2班植树的棵数是（　　）

A．36           B．60             C．100               D．180

3.如图，直线a∥b，∠1＝55°，则∠2的度数是（　　）

A．35°          B．45°          C．55°               D．125°

4.四张背面完全相同的卡片，正面分别印有等腰三角形、圆、平行四边形、正六边形，现在把它们的正面向下，随机的摆放在桌面上，从中任意抽出一张，则抽到的卡片正面是中心对称图形的概率是（    ）

A．                   D．1

5.勾股定理是“人类最伟大的十个科学发现之一”．我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的，他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽．下列图案中是“赵爽弦图”的是（　　）

A．            B．         C．      D．

6.下列各数轴上表示的x的取值范围可以是不等式组的解集的是（　　）

A．       B．   

C．       D．

7.如图，在△ABC中，AB＝AC＝8．点E，F，G分别在边AB，BC，AC上，EF∥AC，GF∥AB，则四边形AEFG的周长是（　　）

A．32              B．24             C．16                D．8

8. “双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（　　）

A．4种            B．5种             C．6种             D．7种

9.定义一种对正整数n的“F”运算：①当n为奇数时，F（n）=3n+1；②当n为偶数时，F（n）=（其中k是使F（n）为奇数的正整数）……，两种运算交替重复进行，例如，取n=24，则：

若n=13，则第2018次“F”运算的结果是（　　）

A．1             B．4              C．2018               D．42018

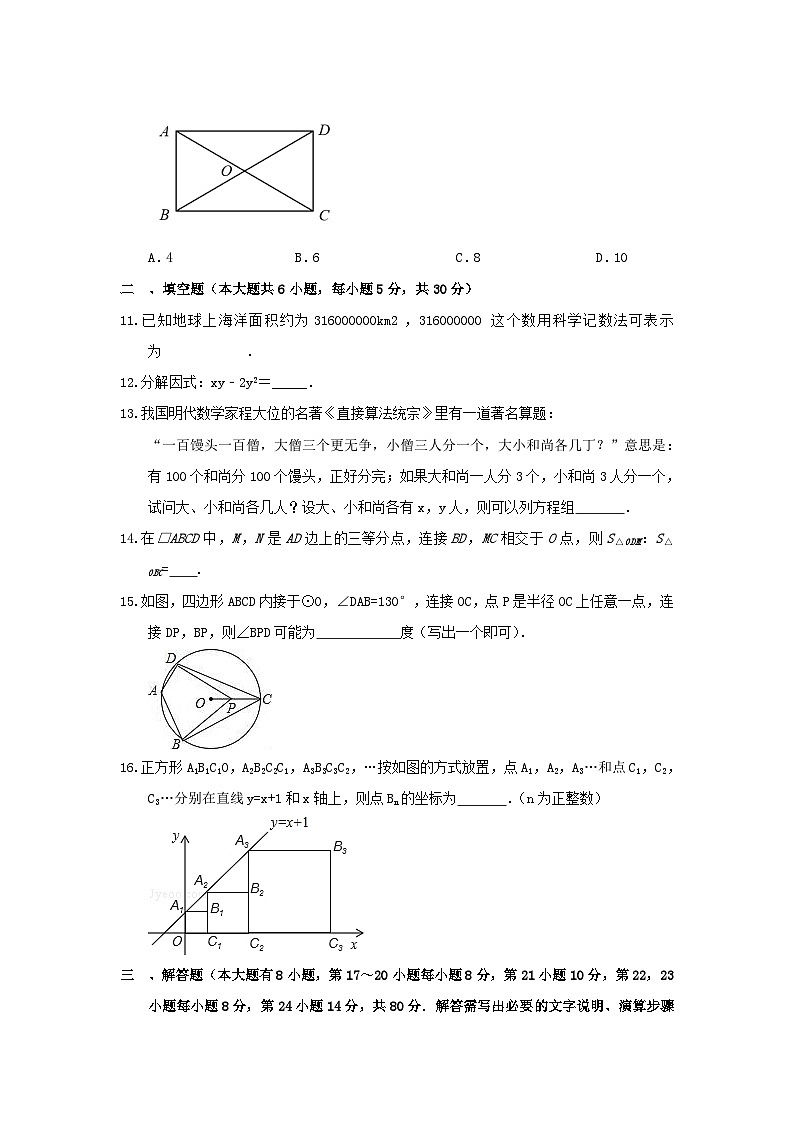
10.在矩形中，、相交于点，若的面积为2，则矩形的面积为（    ）

A．4                  B．6                 C．8                 D．10

二       、填空题（本大题共6小题，每小题5分，共30分）

11.已知地球上海洋面积约为316000000km2，316000000这个数用科学记数法可表示为　　　　　　．

12.分解因式：xy﹣2y2＝_____．

13.我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题：

“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，正好分完；如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各几人？设大、小和尚各有x，y人，则可以列方程组　   　．

14.在□ABCD中，M，N是AD边上的三等分点，连接BD，MC相交于O点，则S△ODM：S△OBC=    .

15.如图，四边形ABCD内接于⊙O，∠DAB=130°，连接OC，点P是半径OC上任意一点，连接DP，BP，则∠BPD可能为　　　　　　度（写出一个即可）．

16.正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置，点A1，A2，A3…和点C1，C2，C3…分别在直线y=x+1和x轴上，则点Bn的坐标为　   　．（n为正整数）

三       、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题8分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17.（1）先化简再求值：（m+2﹣）×，其中m＝4．

（2）解不等式组并将解集表示在所给的数轴上．

18.如图，在▱ABCD中，对角线AC，BD相交于点O，AB＝AD．

（1）求证：AC⊥BD，

（2）若点E，F分别为AD，AO的中点，连接EF，EF＝，AO＝2，求BD的长及四边形ABCD的周长．

19.某企业为推进全民健身活动，提升员工身体素质，号召员工开展健身锻炼活动，经过两个月的宣传发动，员工健身锻炼的意识有了显著提高．为了调查本企业员工上月参加健身锻炼的情况，现从1500名员工中随机抽取200人调查每人上月健身锻炼的次数，并将调查所得的数据整理如下：

某企业员工参加健身锻炼次数的频数分布表

某企业员工参加健身锻炼次数的扇形统计图

（1）表格中________；

（2）请把扇形统计图补充完整；（只需标注相应的数据）

（3）请估计该企业上月参加健身锻炼超过10次的员工有多少人？

20.政府将要在某学校大楼前修一座大桥．如图，宋老师测得大楼的高是20米，大楼的底部D处与将要修的大桥BC位于同一水平线上，宋老师又上到楼顶A处测得B和C的俯角，分别为和，宋老师说现在我能算出将要修的大桥BC的长了．同学们：你知道宋老师是怎么算的吗？请写出计算过程（结果精确到0.1米）．其中，，，，，

21.杠杆原理在生活中被广泛应用（杠杆原理：阻力×阻力臂＝动力×动力臂），小明利用这一原理制作了一个称量物体质量的简易“秤”（如图1）．制作方法如下：

第一步：在一根匀质细木杆上标上均匀的刻度（单位长度1cm），确定支点O，并用细麻绳固定，在支点O左侧2cm的A处固定一个金属吊钩，作为秤钩，

第二步：取一个质量为0.5kg的金属物体作为秤砣．

（1）图1中，把重物挂在秤钩上，秤砣挂在支点O右侧的B处，秤杆平衡，就能称得重物的质量．当重物的质量变化时，OB的长度随之变化．设重物的质量为xkg，OB的长为ycm．写出y关于x的函数解析式，若0＜y＜48，求x的取值范围．

（2）调换秤砣与重物的位置，把秤砣挂在秤钩上，重物挂在支点O右侧的B处，使秤杆平衡，如图2．设重物的质量为xkg，OB的长为ycm，写出y关于x的函数解析式，完成下表，画出该函数的图象．

22.请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．

（1）如图①，四边形ABCD中，AB＝AD，∠B＝∠D，画出四边形ABCD的对称轴m，

（2）如图②，四边形ABCD中，AD∥BC，∠A＝∠D，画出BC边的垂直平分线n．

23.已知抛物线y＝ax2+bx+c经过A（2，0），B（3n﹣4，y1），C（5n+6，y2）三点，对称轴是直线x＝1．关于x的方程ax2+bx+c＝x有两个相等的实数根．

（1）求抛物线的解析式；

（2）若n＜﹣5，试比较y1与y2的大小；

（3）若B，C两点在直线x＝1的两侧，且y1＞y2，求n的取值范围．

24.如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P．

（1）求证：PD是⊙O的切线；

（2）求证：△PBD∽△DCA；

（3）当AB=6，AC=8时，求线段PB的长．

答案解析

一       、选择题

1.【考点】简单几何体的三视图

【分析】根据简单几何体的三视图的画法，看得见的轮廓线用实线表示，看不见的轮廓线用虚线表示可得答案．

解：从左面看该几何体，选项C中的图形符合题意，

故选：C．

【点评】本题考查简单几何体的三视图，理解视图的意义是正确判断的前提，掌握看得见的轮廓线用实线表示，看不见的轮廓线用虚线表示是得出正确答案的关键．

2.【考点】有理数的混合运算．

【分析】根据题目当中信息列式计算即可．

解：七年级2班植树棵数：＝＝＝100（棵），

故选：C．

【点评】本题考查有理数的混合运算，准确的约分是关键．

3.【考点】平行线的性质．

【分析】根据两直线平行，同位角相等可得∠3＝∠1，再根据对顶角相等可得∠2＝∠3．

解：如图，∵a∥b，

∴∠3＝∠1＝55°，

∴∠2＝∠3＝55°．

故选：C．

【点评】本题考查了平行线的性质，对顶角相等的性质，熟记性质是解题的关键．

4.【考点】概率公式

【分析】由四张质地、大小、背面完全相同的卡片上，正面分别画有等腰三角形、圆、平行四边形、正六边形四个图案．中心对称图形的是圆、平行四边形，正六边形，直接利用概率公式求解即可求得答案．

解：∵四张质地、大小、背面完全相同的卡片上，正面分别画有等腰三角形、圆、平行四边形、正六边形四个图案．中心对称图形的是圆、平行四边形，正六边形，

∴从中任意抽出一张，则抽出的卡片正面图案是中心对称图形的概率为：．

故选：C．

【点评】此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．

5.【考点】勾股定理的证明

【分析】“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形．

解：“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形，如图所示：

故选：B．

【点评】本题主要考查了勾股定理的证明，证明勾股定理时，用几个全等的直角三角形拼成一个规则的图形，然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理．

6.【考点】在数轴上表示不等式的解集，解一元一次不等式组

【分析】由数轴上解集左端点得出a的值，代入第二个不等式，解之求出x的另外一个范围，结合数轴即可判断．

解：由x+2＞a得x＞a﹣2，

A．由数轴知x＞﹣3，则a＝﹣1，∴﹣3x﹣6＜0，解得x＞﹣2，与数轴不符，

B．由数轴知x＞0，则a＝2，∴3x﹣6＜0，解得x＜2，与数轴相符合，

C．由数轴知x＞2，则a＝4，∴7x﹣6＜0，解得x＜，与数轴不符，

D．由数轴知x＞﹣2，则a＝0，∴﹣x﹣6＜0，解得x＞﹣6，与数轴不符，

故选：B．

【点评】本题主要考查解一元一次不等式组，解题的关键是掌握不等式组的解集在数轴上的表示及解一元一次不等式的能力．

7.【考点】平行四边形的判定与性质；等腰三角形的性质．

【分析】根据EF∥AC，GF∥AB，可以得到四边形AEFG是平行四边形，∠B＝∠GFC，∠C＝∠EFB，再根据AB＝AC＝8和等量代换，即可求得四边形AEFG的周长．

解：∵EF∥AC，GF∥AB，

∴四边形AEFG是平行四边形，∠B＝∠GFC，∠C＝∠EFB，

∵AB＝AC，

∴∠B＝∠C，

∴∠B＝∠EFB，∠GFC＝∠C，

∴EB＝EF，FG＝GC，

∵四边形AEFG的周长是AE+EF+FG+AG，

∴四边形AEFG的周长是AE+EB+GC+AG＝AB+AC，

∵AB＝AC＝8，

∴四边形AEFG的周长是AG+AC＝8+8＝16，

故选：C．

【点评】本题考查平行四边形的判定与性质、等腰三角形的性质，解答本题的关键是明确题意，将平行四边形的周长转化为AB和AC的关系．

8.【考点】 二元一次方程的应用．

【分析】设购买80元的商品数量为x，购买120元的商品数量为y，根据总费用是1000元列出方程，求得正整数x、y的值即可．

解：设购买80元的商品数量为x，购买120元的商品数量为y，

依题意得：80x+120y=1000，

整理，得

y=．

因为x是正整数，

所以当x=2时，y=7．

当x=5时，y=5．

当x=8时，y=3．

当x=11时，y=1．

即有4种购买方案．

故选：A．

【点评】本题考查了二元一次方程的应用．对于此类问题，挖掘题目中的关系，找出等量关系，列出二元一次方程．然后根据未知数的实际意义求其整数解．　

9.【考点】数字的变化类

【分析】计算出n=13时第一、二、三、四、五、六次运算的结果，找出规律再进行解答即可．

解：若n=13，

第1次结果为：3n+1=40，

第2次结果是： =5，

第3次结果为：3n+1=16，

第4次结果为： =1，

第5次结果为：4，

第6次结果为：1，

…

可以看出，从第四次开始，结果就只是1，4两个数轮流出现，

且当次数为偶数时，结果是1；次数是奇数时，结果是4，

而2018次是偶数，因此最后结果是1．

故选：A．

【点评】本题主要考查了数字的变化类，能根据所给条件得出n=13时六次的运算结果，找出规律是解答此题的关键．

10.【考点】矩形的性质

【分析】根据矩形的性质得到OA=OB=OC=OD，推出，即可求出矩形ABCD的面积.

解：∵四边形ABCD是矩形，对角线、相交于点，

∴AC=BD，且OA=OB=OC=OD，

∴,

∴矩形的面积为,

故选：C.

【点评】此题考查矩形的性质：矩形的对角线相等，且互相平分，由此可以将矩形的；面积四等分，由此可以解决问题，熟记矩形的性质定理是解题的关键.

二       、填空题

11.【考点】 科学记数法—表示较大的数．

【分析】根据科学记数法定义得到316000000这个数用科学记数法可表示3.16×108．

解：316000000=3.16×108．

故答案为3.16×108．

【点评】 本题考查了科学记数法﹣表示较大的数：用a×10n（1≤a＜10，n为整数）表示较大数的方法叫科学记数法．

12.【考点】因式分解-提公因式法

【分析】用提公因式法进行因式分解即可．

解：xy﹣2y2＝y（x﹣2y），

故答案为：y（x﹣2y）．

【点评】本题考查提公因式法因式分解，找出公因式是正确分解的前提．

13.【考点】由实际问题抽象出二元一次方程组．

【分析】分别利用大、小和尚一共100人以及馒头大和尚一人分3个，小和尚3人分一个，馒头一共100个分别得出等式得出答案．

解：设大、小和尚各有x，y人，则可以列方程组：

．

故答案为：．

【点评】此题主要考查了由实际问题抽象出二元一次方程组，正确得出等量关系是解题关键．　

14.【考点】相似三角形的判定与性质；平行四边形的性质．

【分析】首先根据M，N是AD边上的三等分点，判断出＝或＝；然后根据四边

形ABCD是平行四边形，判断出AD∥BC，△MOD∽△C0B，据此求出S△MOD：S△COB的值是多少即

可．

解：∵M，N是AD边上的三等分点，

（1）当＝时，如图1，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴△MOD∽△C0B，

∴S△MOD：S△COB=（）2=4：9．

（2）当＝时，如图2，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴△MOD∽△C0B，

∴S△MOD：S△COB=（＝）2=1：9．

故答案为：4：9或1：9．

【点评】（1）此题主要考查了相似三角形的性质和应用，要熟练掌握，解答此题的关键是要

明确：寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形

进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有时可单独使用，有

时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．

（2）此题还考查了平行四边形的性质和应用，要熟练掌握，解答此题的关键是要明确平行

四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：

平行四边形的对角线互相平分．

（3）此题还考查了三角形的面积的求法，要熟练掌握，解答此题的关键是要明确：三角形

的高一定时，三角形的面积和底成正比．

15.【考点】圆内接四边形的性质；圆周角定理．

【分析】连接OB、OD，根据圆内接四边形的性质求出∠DCB的度数，根据圆周角定理求出∠DOB的度数，得到∠DCB＜∠BPD＜∠DOB．

解：连接OB、OD，

∵四边形ABCD内接于⊙O，∠DAB=130°，

∴∠DCB=180°﹣130°=50°，

由圆周角定理得，∠DOB=2∠DCB=100°，

∴∠DCB＜∠BPD＜∠DOB，即50°＜∠BPD＜100°，

∴∠BPD可能为80°，

故答案为：80．

【点评】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．　

16.【考点】规律型：点的坐标；一次函数图象上点的坐标特征

【分析】根据一次函数图象上点的坐标特征可得出点A1的坐标，结合正方形的性质可得出点B1的坐标，同理可得出点B2、B3、B4、…的坐标，再根据点的坐标的变化即可找出点Bn的坐标．

解：当x=0时，y=x+1=1，

∴点A1的坐标为（0，1）．

∵四边形A1B1C1O为正方形，

∴点B1的坐标为（1，1）．

当x=1时，y=x+1=2，

∴点A2的坐标为（1，2）．

∵四边形A2B2C2C1为正方形，

∴点B2的坐标为（3，2）．

同理可得：点A3的坐标为（3，4），点B3的坐标为（7，4），点A4的坐标为（7，8），点B4的坐标为（15，8），…，

∴点Bn的坐标为（2n﹣1，2n﹣1）．

故答案为：（2n﹣1，2n﹣1）．

【点评】本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型中点的坐标，根据一次函数图象上点的坐标特征结合正方形的性质找出点Bn的坐标是解题的关键．

三       、解答题

17.【考点】分式的化简求值，在数轴上表示不等式的解集，解一元一次不等式组．

【分析】（1）直接将括号里面通分运算，再利用分式的混合运算法则化简得出答案，

（2）直接解不等式，进而得出不等式组的解集，进而得出答案．

解：（1）原式＝×

＝×

＝（m﹣3）（m﹣1）

＝m2﹣4m+3，

当m＝4时，

原式＝42﹣4×4+3

＝3，

（2），

解①得：x＞2，

解②得：x≤4，

故不等式组的解集是：2＜x≤4，

解集在数轴上表示：

．

【点评】此题主要考查了分式的化简求值以及解一元一次不等式组，正确掌握相关运算法则是解题关键．

18.【考点】平行四边形的性质，三角形中位线定理．

【分析】（1）由菱形的判定得▱ABCD是菱形，再由菱形的性质即可得出结论，

（2）由三角形中位线定理得OD＝2EF＝3，再由菱形的性质得AB＝BC＝CD＝AD，AC⊥

BD，BD＝2OD＝6，然后由勾股定理得AD＝，即可求出菱形ABCD的周长．

（1）证明：∵四边形ABCD是平行四边形，AB＝AD，

∴▱ABCD是菱形，

∴AC⊥BD，

（2）解：∵点E，F分别为AD，AO的中点，

∴EF是△AOD的中位线，

∴OD＝2EF＝3，

由（1）可知，四边形ABCD是菱形，

∴AB＝BC＝CD＝AD，AC⊥BD，BD＝2OD＝6，

在Rt△AOD中，由勾股定理得：AD＝＝＝，

∴菱形ABCD的周长＝4AD＝4．

【点评】本题考查了平行四边形的性质、菱形的判定与性质、三角形中位线定理以及

勾股定理等知识，熟练掌握菱形的判定与性质是解题的关键．

19.【考点】扇形统计图，频数分布表

【分析】（1）由扇形统计图直接得出b的值，再用200×b，即可求解；

（2）先算出c，d的值，再补充统计图，即可；

（3）用总人数×健身锻炼超过10次的员工的频率之和，即可求解．

（1）解：由扇形统计图可知：b=0.21，a=200×0.21=42，

故答案是：42；

（2）c=200-10-42-68-24-6=50，d=50÷200×100％=25％，

补全扇形统计图如下：

（3）1500×(0.34+0.25+0.12+0.03)=1110（人），

答：估计该企业上月参加健身锻炼超过10次的员工有1110人．

【点评】本题主要考查扇形统计图以及频数分布表，准确找出相关数据，是解题的关键．

20.【考点】解直角三角形的应用-仰角俯角问题

【分析】根据AE∥DB,确定∠ABD=67°，∠ACD=22°，利用正切函数求得DB，DC的长度即可求解.

解：如图，∵AE∥DB,

∴∠ABD=67°，∠ACD=22°，

∵tan∠ABD=，tan∠ACD=，

∴DB==，DC==50，

∴BC=DC-DB=50-≈41.7（米）.

【点评】本题考查了俯角的意义，解直角三角形，准确理解俯角的意义，熟练运用三角函数是解题的关键．

21.【考点】反比例函数的应用．

【分析】（1）根据阻力×阻力臂＝动力×动力臂解答即可，

（2）根据阻力×阻力臂＝动力×动力臂求出解析式，然后根据列表、描点、连线的步骤解答．

解：（1）∵阻力×阻力臂＝动力×动力臂，

∴重物×OA＝秤砣×OB，

∵OA＝2cm，重物的质量为xkg，OB的长为ycm，秤砣为0.5kg，

∴2x＝0.5y，

∴y＝4x，

∵4＞0，

∴y随x的增大而增大，

∵当y＝0时，x＝0，

当y＝48时，x＝12，

∴0＜x＜12，

（2）∵阻力×阻力臂＝动力×动力臂，

∴秤砣×OA＝重物×OB，

∵OA＝2cm，重物的质量为xkg，OB的长为ycm，秤砣为0.5kg，

∴2×0.5＝xy，

∴y＝，

当x＝0.25时，y＝＝4，

当x＝0.5时，y＝＝2，

当x＝1时，y＝1，

当x＝2时，y＝，

当x＝4时，y＝，

故答案为：4，2，1，，，

作函数图象如图：

【点评】本题考查了一次函数和反比例函数的应用，以及列表、描点、连线画函数图象的方法，求出函数解析式是解答本题的关键．

22.【考点】平行线的判定，线段垂直平分线的性质，作图﹣轴对称变换

【分析】（1）连接AC，AC所在直线即为对称轴m．

（2）延长BA，CD交于一点，连接AC，BC交于一点，连接两点获得垂直平分线n．

解：（1）如图①，直线m即为所求

（2）如图②，直线n即为所求

【点评】本题考查了轴对称作图，根据全等关系可以确定点与点的对称关系，从而确定对称轴所在，即可画出直线．

23.【考点】抛物线与x轴的交点，二次函数的性质，根的判别式，待定系数法求二次函数的解析式，一元一次不等式组的应用

【分析】（1）由题意可得0=4a+2b+c①，②，△=（b-1）2-4ac=0③，联立方程组可求a，b，c，可求解析式；

（2）由n＜-5，可得点B，点C在对称轴直线x=1的左侧，由二次函数的性质可求解；

（3）分两种情况讨论，列出不等式组可求解．

解：（1）∵抛物线y＝ax2+bx+c经过A（2，0），

∴0＝4a+2b+c①，

∵对称轴是直线x＝1，

∴②，

∵关于x的方程ax2+bx+c＝x有两个相等的实数根，

∴△＝（b﹣1）2﹣4ac＝0③，

由①②③可得：，

∴抛物线的解析式为y＝﹣x2+x；

（2）∵n＜﹣5，

∴3n﹣4＜﹣19，5n+6＜﹣19

∴点B，点C在对称轴直线x＝1的左侧，

∵抛物线y＝﹣x2+x，

∴﹣＜0，即在对称轴的左侧y随x的增大而增大，

∵（3n﹣4）﹣（5n+6）＝﹣2n﹣10＝﹣2（n+5）＞0，

∴3n﹣4＞5n+6，

∴y1＞y2；

（3）若点B在对称轴直线x＝1的左侧，点C在对称轴直线x＝1的右侧时，

由题意可得，

∴0＜n＜，

若点C在对称轴直线x＝1的左侧，点B在对称轴直线x＝1的右侧时，

由题意可得：，

∴不等式组无解，

综上所述：0＜n＜．

【点评】本题考查了抛物线与x轴的交点，二次函数的性质，根的判别式，待定系数法求解析式，一元一次不等式组的应用，利用分类讨论思想解决问题是本题的关键．

24.【考点】 相似三角形的判定与性质； 切线的判定与性质．

【分析】（1）由直径所对的圆周角为直角得到∠BAC为直角，再由AD为角平分线，得到一对角相等，根据同弧所对的圆心角等于圆周角的2倍及等量代换确定出∠DOC为直角，与平行线中的一条垂直，与另一条也垂直得到OD与PD垂直，即可得证；

（2）由PD与BC平行，得到一对同位角相等，再由同弧所对的圆周角相等及等量代换得到∠P=∠ACD，根据同角的补角相等得到一对角相等，利用两对角相等的三角形相似即可得证；

（3）由三角形ABC为直角三角形，利用勾股定理求出BC的长，再由OD垂直平分BC，得到DB=DC，根据（2）的相似，得比例，求出所求即可．

（1）证明：∵圆心O在BC上，

∴BC是圆O的直径，

∴∠BAC=90°，

连接OD，

∵AD平分∠BAC，

∴∠BAC=2∠DAC，

∵∠DOC=2∠DAC，

∴∠DOC=∠BAC=90°，即OD⊥BC，

∵PD∥BC，

∴OD⊥PD，

∵OD为圆O的半径，

∴PD是圆O的切线；

（2）证明：∵PD∥BC，

∴∠P=∠ABC，

∵∠ABC=∠ADC，

∴∠P=∠ADC，

∵∠PBD+∠ABD=180°，∠ACD+∠ABD=180°，

∴∠PBD=∠ACD，

∴△PBD∽△DCA；

（3）解：∵△ABC为直角三角形，

∴BC2=AB2+AC2=62+82=100，

∴BC=10，

∵OD垂直平分BC，

∴DB=DC，

∵BC为圆O的直径，

∴∠BDC=90°，

在Rt△DBC中，DB2+DC2=BC2，即2DC2=BC2=100，

∴DC=DB=5，

∵△PBD∽△DCA，

∴=，

则PB===．