2022-2023学年福建省泉州五中八年级（下）期中数学试卷(含解析)

这是一份2022-2023学年福建省泉州五中八年级（下）期中数学试卷(含解析)，共24页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

2022-2023学年福建省泉州五中八年级（下）期中数学试卷
一、选择题
1．使分式有意义的x的取值范围是（　　）
A．x≠0 B．x＞2 C．x＜2 D．x≠2
2．如图，在平行四边形ABCD中，∠A﹣∠B＝50°，则∠A的度数是（　　）

A．130° B．115° C．65° D．50°
3．下列各分式中，是最简分式的是（　　）
A． B． C． D．
4．在四边形ABCD中，下列不能判断它是平行四边形的是（　　）
A．AB∥CD，AD∥BC B．AB＝CD，AD＝BC
C．AB∥CD，AB＝CD D．AB∥CD，AD＝BC
5．已知一元二次方程x2﹣3x+1＝0有两个实数根x1，x2，则x1+x2﹣x1x2的值为（　　）
A．6 B．2 C．4 D．3
6．如图，E是矩形ABCD的边DC上一点，AB＝AE，∠AED＝30°，则∠BEC等于（　　）

A．60° B．70° C．75° D．80°
7．如图，在平行四边形ABCD中，M、N是BD上两点，BM＝DN，连接AM、MC、CN、NA，添加一个条件，使四边形AMCN是矩形，这个条件是（　　）

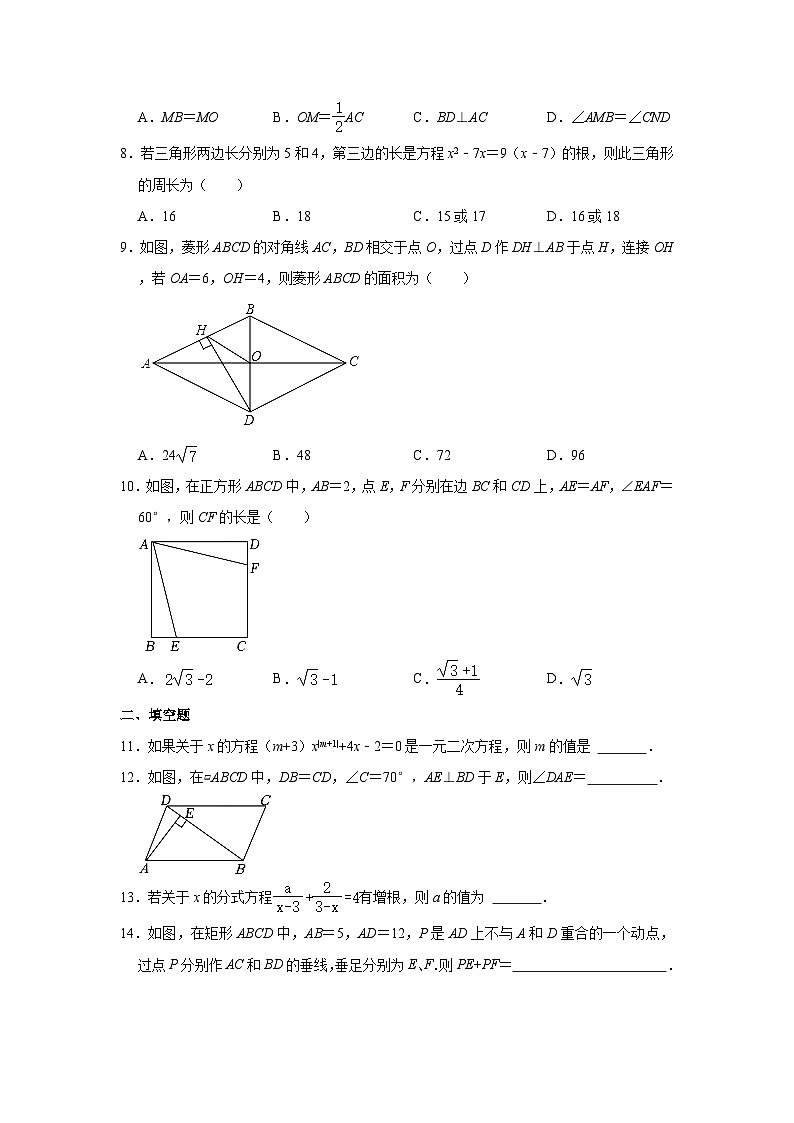
A．MB＝MO B．OM＝AC C．BD⊥AC D．∠AMB＝∠CND
8．若三角形两边长分别为5和4，第三边的长是方程x2﹣7x＝9（x﹣7）的根，则此三角形的周长为（　　）
A．16 B．18 C．15或17 D．16或18
9．如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，OH＝4，则菱形ABCD的面积为（　　）

A．24 B．48 C．72 D．96
10．如图，在正方形ABCD中，AB＝2，点E，F分别在边BC和CD上，AE＝AF，∠EAF＝60°，则CF的长是（　　）

A． B． C． D．
二、填空题
11．如果关于x的方程（m+3）x|m+1|+4x﹣2＝0是一元二次方程，则m的值是 　 　．
12．如图，在▱ABCD中，DB＝CD，∠C＝70°，AE⊥BD于E，则∠DAE＝　 　．

13．若关于x的分式方程有增根，则a的值为 　 　．
14．如图，在矩形ABCD中，AB＝5，AD＝12，P是AD上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足分别为E、F．则PE+PF＝　 　．

15．如图，菱形ABCD中，∠ABC＝60°，AB＝2，E、F分别是边BC和对角线BD上的动点，且BE＝DF，则AE+AF的最小值为 　 　．

三.解答题（共9小题，满分86分）
16．计算：（﹣1）2023+（π﹣3.14）0×（﹣2）2+（）﹣2．
17．解方程：x2﹣2x﹣3＝0．
18．先化简再求值：，其中x＝1．
19．如图，在▱ABCD中，AH⊥BD于H，CG⊥BD于G，连接CH和AG，求证：∠1＝∠2．

20．如图，在平行四边形ABCD中，连接BD，E为线段AD的中点，延长BE与CD的延长线交于点F，连接AF，∠BDF＝90°．
（1）求证：四边形ABDF是矩形；
（2）若AD＝10，BD＝8，求△BCF的面积．

21．已知关于x的一元二次方程kx2﹣（k+8）x+8＝0．
（1）求证：无论k取任何非零实数，方程总有实数根；
（2）若等腰三角形的一边长为4，另两边长恰好是这个方程的两个根，求此时的k值．
22．某乡准备修一条长15千米的乡村公路．该工程将由甲工程队或乙工程队单独完成．甲工程队每天比乙工程队多修路0.5千米．
（1）设乙工程队每天修路x千米．请用含x的代数式填表：
工程队
甲
乙
单独完成所需天数/天
　 　
　 　
（2）已知甲、乙两工程队每天的修路费用分别为1万元、0.8万元，若甲和乙单独完成这项工程所需费用相同，求单独完成这项工程甲工程队比乙工程队少用的天数．
23．请阅读下列材料：x2+x﹣1＝0，求一个一元二次方程，使它的根分别是已知方程根的2倍．解：设所求方程的根为y，则y＝2x，所以，把代入已知方程，得，化简，得y2+2y﹣4＝0，故所求方程为y2+2y﹣4＝0，这种利用方程的代换求新方程的方法，我们称为“换根法”．请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）．
（1）已知方程x2+x﹣2＝0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为：　 　；
（2）已知方程2x2﹣7x+3＝0，求一个一元二次方程，使它的根分别是已知方程根的倒数；
（3）已知关于x的一元二次方程ax2+bx+c＝0（a≠0）的两个实数根分别为3，﹣2，求一元二次方程ay2﹣（2a﹣b）y+a﹣b+c＝0的两根．（直接写出结果）
24．将正方形ABCD的边CD绕点C顺时针旋转α°（0＜α＜90）至CP，连接PB，PD．
（1）如图1，当α＝40°时，直接写出∠BPD的大小；
（2）如图2，过点B作BE⊥PD交PD延长线于点E，连接AE．
①求∠BPD的大小；
②探究AE，PD之间的数量关系，并证明你的结论；
③当点D为PE中点时，PB＝6，直接写出四边形ABPE的面积．



参考答案
一、选择题
1．使分式有意义的x的取值范围是（　　）
A．x≠0 B．x＞2 C．x＜2 D．x≠2
【分析】分式有意义的条件是分母不等于零，据此求出x的取值范围即可．
解：∵分式有意义，
∴x﹣2≠0，
解得x≠2．
故选：D．
【点评】此题主要考查了分式有意义的条件，解答此题的关键是要明确：分式有意义的条件是分母不等于零．
2．如图，在平行四边形ABCD中，∠A﹣∠B＝50°，则∠A的度数是（　　）

A．130° B．115° C．65° D．50°
【分析】利用平行四边形的邻角互补和已知∠A﹣∠B＝50°，就可建立方程求出未知角．
解：在平行四边形ABCD中，∠A+∠B＝180°，
又有∠A﹣∠B＝50°，
把这两个式子相加即可求出∠A＝115°，
故选：B．
【点评】本题考查了平行四边形的性质：邻角互补，建立方程组求解．
3．下列各分式中，是最简分式的是（　　）
A． B． C． D．
【分析】直接利用最简分式的定义，一个分式的分子与分母没有公因式时叫最简分式，进而分析得出答案．
解：A．＝，故此选项不合题意；
B．＝，故此选项不合题意；
C．＝x﹣y，故此选项不合题意；
D．，是最简分式，故此选项符合题意．
故选：D．
【点评】此题主要考查了最简分式，正确掌握最简分式的定义是解题关键．
4．在四边形ABCD中，下列不能判断它是平行四边形的是（　　）
A．AB∥CD，AD∥BC B．AB＝CD，AD＝BC
C．AB∥CD，AB＝CD D．AB∥CD，AD＝BC
【分析】根据平行四边形的判定方法，进行判断即可．
解：A、根据两组对边分别平行的四边形是平行四边形，即可得到四边形ABCD是平行四边形，不符合题意；
B、根据两组对边分别相等的四边形是平行四边形，即可得到四边形ABCD是平行四边形，不符合题意；
C、根据一组对边平行且相等的四边形是平行四边形，即可得到四边形ABCD是平行四边形，不符合题意；
D、不能证明四边形ABCD是平行四边形，符合题意；
故选：D．
【点评】本题考查平行四边形的判定．熟练掌握平行四边形的判定方法，是解题的关键．
5．已知一元二次方程x2﹣3x+1＝0有两个实数根x1，x2，则x1+x2﹣x1x2的值为（　　）
A．6 B．2 C．4 D．3
【分析】先根据根与系数的关系得x1+x2＝3，x1x2＝﹣1，然后利用整体代入的方法计算．
解：根据根与系数的关系得x1+x2＝3，x1x2＝1，
所以x1+x2﹣x1x2＝3﹣1＝2．
故选：B．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根，则x1+x2＝﹣，x1x2＝．
6．如图，E是矩形ABCD的边DC上一点，AB＝AE，∠AED＝30°，则∠BEC等于（　　）

A．60° B．70° C．75° D．80°
【分析】直接利用矩形的性质结合锐角三角函数关系得出∠AEB的度数即可得出答案．
解：∵四边形ABCD是矩形，
∴AB∥DC，
∴∠DEA＝∠EAB＝30°，
∵AB＝AE，∠AED＝30°，
∴∠ABE＝∠AEB＝75°，
∴∠BEC＝180°﹣∠AEB﹣∠AED＝75°，
故选：C．
【点评】此题主要考查了矩形的性质，掌握矩形的性质以及等腰三角形的性质是解题的关键．
7．如图，在平行四边形ABCD中，M、N是BD上两点，BM＝DN，连接AM、MC、CN、NA，添加一个条件，使四边形AMCN是矩形，这个条件是（　　）

A．MB＝MO B．OM＝AC C．BD⊥AC D．∠AMB＝∠CND
【分析】由平行四边形的性质可知，OA＝OC，OB＝OD，再证OM＝ON，则四边形AMCN是平行四边形，然后证MN＝AC，即可得出结论．
解：添加一个条件，使四边形AMCN是矩形，这个条件是OM＝AC，理由如下：
∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
∵对角线BD上的两点M、N满足BM＝DN，
∴OB﹣BM＝OD﹣DN，
即OM＝ON，
∴四边形AMCN是平行四边形，
∵OM＝AC，
∴MN＝AC，
∴四边形AMCN是矩形．
故选：B．
【点评】本题考查了矩形的判定，平行四边形的判定与性质，熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．
8．若三角形两边长分别为5和4，第三边的长是方程x2﹣7x＝9（x﹣7）的根，则此三角形的周长为（　　）
A．16 B．18 C．15或17 D．16或18
【分析】首先求出方程的根，再根据三角形三边关系定理，确定第三边的长，进而求其周长．
解：将x2﹣7x＝9（x﹣7）变形为（x﹣7）（x﹣9）＝0，
解得：x1＝7，x2＝9，
∵三角形两边长分别为5和4，
∴5﹣4＜第三边的边长＜5+4，
即第三边的边长在1和9之间，
∴第三边的边长为7．
∴这个三角形的周长是4+5+7＝16．
故选：A．
【点评】本题考查因式分解法解一元二次方程、三角形的三边关系，解题的关键在于根据三角形三边关系对一元二次方程的根进行取舍．
9．如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，OH＝4，则菱形ABCD的面积为（　　）

A．24 B．48 C．72 D．96
【分析】由菱形的性质得OA＝OC＝6，OB＝OD，AC⊥BD，则AC＝12，再由直角三角形斜边上的中线性质求出BD的长度，然后由菱形的面积公式求解即可．
解：∵四边形ABCD是菱形，
∴OA＝OC＝6，OB＝OD，AC⊥BD，
∴AC＝12，
∵DH⊥AB，
∴∠BHD＝90°，
∴BD＝2OH＝2×4＝8，
∴菱形ABCD的面积＝AC•BD＝×12×8＝48，
故选：B．
【点评】本题主要考查了菱形的性质，直角三角形的斜边上的中线性质，菱形的面积公式等知识；熟练掌握菱形的性质，求出BD的长是解题的关键．
10．如图，在正方形ABCD中，AB＝2，点E，F分别在边BC和CD上，AE＝AF，∠EAF＝60°，则CF的长是（　　）

A． B． C． D．
【分析】由正方形的性质得出∠B＝∠D＝∠BAD＝90°，AB＝BC＝CD＝AD＝2，证明Rt△ABE≌Rt△ADF得出∠BAE＝∠DAF，求出∠DAF＝15°，在AD上取一点G，使∠GFA＝∠DAF＝15°，则AG＝FG，∠DGF＝30°，由直角三角形的性质得出DF＝FG＝AG，DG＝DF，设DF＝x，则DG＝x，AG＝FG＝2x，则2x+x＝2，解得：x＝4﹣2，得出DF＝4﹣2，即可得出结果．
解：∵四边形ABCD是正方形，
∴∠B＝∠D＝∠BAD＝90°，AB＝BC＝CD＝AD＝2，
在Rt△ABE和Rt△ADF中，
，
∴Rt△ABE≌Rt△ADF（HL），
∴∠BAE＝∠DAF，
∵∠EAF＝60°，
∴∠BAE+∠DAF＝30°，
∴∠DAF＝15°，
在AD上取一点G，使∠GFA＝∠DAF＝15°，如图所示：
∴AG＝FG，∠DGF＝30°，
∴DF＝FG＝AG，DG＝DF，
设DF＝x，则DG＝x，AG＝FG＝2x，
∵AG+DG＝AD，
∴2x+x＝2，
解得：x＝4﹣2，
∴DF＝4﹣2，
∴CF＝CD﹣DF＝2﹣（4﹣2）＝2﹣2；
故选：A．

【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定、直角三角形的性质等知识；熟练掌握正方形的性质，证明三角形全等是解题的关键．
二、填空题
11．如果关于x的方程（m+3）x|m+1|+4x﹣2＝0是一元二次方程，则m的值是 　1　．
【分析】根据题意，由于原方程是一元二次方程，那么有x的次数是2，即|m+1|＝2，系数不等于0，即m+3≠0，联合起来解即可．
解：由题意知，|m+1|＝2，且m+3≠0．
解得m＝1或﹣3且m≠﹣3，
∴m＝1．
故答案是：1．
【点评】本题利用了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c＝0（且a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．
12．如图，在▱ABCD中，DB＝CD，∠C＝70°，AE⊥BD于E，则∠DAE＝　20°　．

【分析】由DB＝CD，得∠DBC＝∠C＝70°，则∠ADE＝∠DBC＝70°，而∠AED＝90°，所以∠DAE＝90°﹣∠ADE＝20°．
解：∵DB＝CD，
∴∠DBC＝∠C＝70°，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADE＝∠DBC＝70°，
∵AE⊥BD于E，
∴∠AED＝90°，
∴∠DAE＝90°﹣∠ADE＝90°﹣70°＝20°，
故答案为：20°．
【点评】此题重点考查等腰三角形的性质、平行四边形的性质、直角三角形的两个锐角互余等知识，由平行四边形的性质求得∠DBC＝∠C＝70°是解题的关键．
13．若关于x的分式方程有增根，则a的值为 　2　．
【分析】分式方程去分母转化为整式方程，由分式方程有增根，确定出x的值，代入整式方程计算即可求出a的值
解：分式方程去分母得：a﹣2＝4x﹣12，
整理得：4x﹣10＝a，
由分式方程有增根，得到x﹣3＝0，即x＝3，
把x＝3代入整式方程得：a＝2，
故答案为：2．
【点评】此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．
14．如图，在矩形ABCD中，AB＝5，AD＝12，P是AD上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足分别为E、F．则PE+PF＝　　．

【分析】首先连接OP．由矩形ABCD的两边AB＝5，AD＝12，可得S矩形ABCD＝AB•AD＝5×12＝60，根据勾股定理可得AC＝BD＝＝13，然后根据S△AOD＝S△AOP+S△DOP，进而可以求得答案．
解：连接OP，如图所示，

∵矩形ABCD的两边AB＝5，AD＝12，
∴S矩形ABCD＝AB•AD＝5×12＝60，OA＝OC，OB＝OD，AC＝BD＝＝13，
∴S△AOD＝S矩形ABCD＝15，OA＝OD＝，
∴S△AOD＝S△AOP+S△DOP＝OA•PE+OD•PF＝OA（PE+PF）＝（PE+PF）＝15，
∴PE+PF＝，
故答案为：．
【点评】本题考查了矩形的性质，解决本题的关键是掌握矩形的性质．
15．如图，菱形ABCD中，∠ABC＝60°，AB＝2，E、F分别是边BC和对角线BD上的动点，且BE＝DF，则AE+AF的最小值为 　2　．

【分析】如图，BC的下方作∠CBT＝30°，在BT上截取BT，使得BT＝AD，连接ET，AT．证明△ADF≌△TBE（SAS），推出AF＝ET，AE+AF＝AE+ET，根据AE+ET≥AT求解即可．
解：如图，BC的下方作∠CBT＝30°，在BT上截取BT，使得BT＝AD，连接ET，AT．

∵四边形ABCD是菱形，∠ABC＝60°，
∴∠ADC＝∠ABC＝60°，∠ADF＝∠ADC＝30°，
∵AD＝BT，∠ADF＝∠TBE＝30°，DF＝BE，
∴△ADF≌△TBE（SAS），
∴AF＝ET，
∵∠ABT＝∠ABC+∠CBT＝60°+30°＝90°，AB＝AD＝BT＝2，
∴AT＝＝＝2，
∴AE+AF＝AE+ET，
∵AE+ET≥AT，
∴AE+AF≥2，
∴AE+AF的最小值为2，
故答案为2．
【点评】本题考查菱形的性质，全等三角形的判定和性质，两点之间线段最短等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考填空题中的压轴题．
三.解答题（共9小题，满分86分）
16．计算：（﹣1）2023+（π﹣3.14）0×（﹣2）2+（）﹣2．
【分析】直接利用零指数幂的性质、负整数指数幂的性质、有理数的乘方运算法则分别化简，进而得出答案．
解：原式＝﹣1+1×4+9
＝﹣1+4+9
＝12．
【点评】此题主要考查了实数的运算，正确化简各数是解题关键．
17．解方程：x2﹣2x﹣3＝0．
【分析】通过观察方程形式，本题可用因式分解法进行解答．
解：原方程可以变形为（x﹣3）（x+1）＝0
x﹣3＝0或x+1＝0
∴x1＝3，x2＝﹣1．
【点评】熟练运用因式分解法解一元二次方程．注意：常数项应分解成两个数的积，且这两个的和应等于一次项系数．
18．先化简再求值：，其中x＝1．
【分析】根据分式的混合运算法则把原式化简，把x的值代入计算即可．
解：原式＝[+]•（x+3）（x﹣3）
＝•（x+3）（x﹣3）
＝x2+9，
当x＝1时，原式＝12+9＝10．
【点评】本题考查的是分式的化简求值，掌握分式的混合运算法则是解题的关键．
19．如图，在▱ABCD中，AH⊥BD于H，CG⊥BD于G，连接CH和AG，求证：∠1＝∠2．

【分析】首先证明AH∥CG，再利用平行四边形的性质证明△ABD≌△CDB（SSS），可得S△ABD＝S△BCD，进而可得AH＝CG，再根据一组对边平行且相等的四边形是平行四边形可得结论．
【解答】证明：∵AH⊥BD，CG⊥BD，
∴AH∥CG，
∵四边形ABCD是平行四边形，
∴CD＝AB，AD＝BC，
在△ADB和△CBD中，
∴△ABD≌△CDB（SSS），
∴S△ABD＝S△BCD，
∴AH＝CG，
∴四边形AGCH为平行四边形，
∴CH∥AG，
∴∠1＝∠2．

【点评】此题主要考查了平行四边形的判定和性质，关键是掌握平行四边形对边相等．
20．如图，在平行四边形ABCD中，连接BD，E为线段AD的中点，延长BE与CD的延长线交于点F，连接AF，∠BDF＝90°．
（1）求证：四边形ABDF是矩形；
（2）若AD＝10，BD＝8，求△BCF的面积．

【分析】（1）证明△AEB≌△DEF（AAS），得AB＝DF，则四边形ABDF是平行四边形，再由∠BDF＝90°，即可得出结论；
（2）由矩形的性质得BF＝AD＝10，再由勾股定理得DF＝6，然后由平行四边形的性质得CD＝AB＝6，则CF＝CD+DF＝12，即可解决问题．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABE＝∠DFE，
∵AE＝DE，∠AEB＝∠DEF，
∴△AEB≌△DEF（AAS），
∴AB＝DF，
∵AB∥DF，
∴四边形ABDF是平行四边形，
∵∠BDF＝90°，
∴平行四边形ABDF是矩形．
（2）解：由（1）得：四边形ABDF是矩形，AB＝DF，
∴BF＝AD＝10，
∴，
则AB＝DF＝6，
∵四边形ABCD是平行四边形，
∴CD＝AB＝6，
∴CF＝CD+DF＝6+6＝12，
∵∠BDF＝90°，
∴BD⊥CF，
∴S△BCF＝CF•BD＝×12×8＝48．
【点评】此题重点考查平行四边形的判定与性质、矩形的判定与性质、勾股定理等知识，熟练掌握矩形的判定与性质是解题的关键．
21．已知关于x的一元二次方程kx2﹣（k+8）x+8＝0．
（1）求证：无论k取任何非零实数，方程总有实数根；
（2）若等腰三角形的一边长为4，另两边长恰好是这个方程的两个根，求此时的k值．
【分析】（1）根据判别式即可求出答案．
（2）根据等腰三角形的性质进行分类讨论，然后方程的解的定义以及三角形的三边关系即可求出k的值．
解：（1）由题意可知：k≠0，
∴Δ＝（k+8）2﹣32k
＝k2+16k+64﹣32k
＝k2﹣16k+64
＝（k﹣8）2≥0，
∴无论k取任何非零实数，方程总有实数根．
（2）当三角形的腰长为4时，设底边为a，
∴x＝4是kx2﹣（k+8）x+8＝0的一根，
∴16k﹣4（k+8）+8＝0，
∴16k﹣4k﹣32+8＝0，
∴k＝2，
∴由根与系数的关系可知：4a＝，
∴a＝1，
此时1+4＞4，能够组成三角形，满足题意，
∴当底边为4时，设腰长为a，
∴kx2﹣（k+8）x+8＝0有两个相同的根，
∴Δ＝（k+8）2﹣32k＝0，
∴k＝8，
∴该方程的解为：x＝1．
∴1+1＜4，不能组成三角形，
综上所述，k＝2．
【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法以及判别式的使用，本题属于中等题型．
22．某乡准备修一条长15千米的乡村公路．该工程将由甲工程队或乙工程队单独完成．甲工程队每天比乙工程队多修路0.5千米．
（1）设乙工程队每天修路x千米．请用含x的代数式填表：
工程队
甲
乙
单独完成所需天数/天
　　
　　
（2）已知甲、乙两工程队每天的修路费用分别为1万元、0.8万元，若甲和乙单独完成这项工程所需费用相同，求单独完成这项工程甲工程队比乙工程队少用的天数．
【分析】（1）由两队工作效率间的关系，可得出甲工程队每天修路（x+0.5）千米，利用工作时间＝工作总量÷工作效率，即可用含x的代数式表示出甲、乙两队单独完成该项工程所需天数；
（2）根据甲和乙单独完成这项工程所需费用相同，可得出关于x的分式方程，解之经检验后可得出x的值，再将其代入﹣中，即可求出结论．
解：（1）∵甲工程队每天比乙工程队多修路0.5千米，乙工程队每天修路x千米，
∴甲工程队每天修路（x+0.5）千米，
∴甲工程队单独完成该工程需要天，乙工程队单独完成该工程需要天．
故答案为：；；
（2）根据题意得：1×＝0.8×，
解得：x＝2，
经检验，x＝2是所列方程的解，且符合题意，
∴﹣＝﹣＝1.5．
答：单独完成这项工程时，甲工程队比乙工程队少用1.5天．
【点评】本题考查了分式方程的应用以及列代数式，解题的关键是：（1）根据各数量之间的关系，用含x的代数式表示出甲、乙两队单独完成该项工程所需天数；（2）找准等量关系，正确列出分式方程．
23．请阅读下列材料：x2+x﹣1＝0，求一个一元二次方程，使它的根分别是已知方程根的2倍．解：设所求方程的根为y，则y＝2x，所以，把代入已知方程，得，化简，得y2+2y﹣4＝0，故所求方程为y2+2y﹣4＝0，这种利用方程的代换求新方程的方法，我们称为“换根法”．请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）．
（1）已知方程x2+x﹣2＝0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为：　y2﹣y﹣2＝0　；
（2）已知方程2x2﹣7x+3＝0，求一个一元二次方程，使它的根分别是已知方程根的倒数；
（3）已知关于x的一元二次方程ax2+bx+c＝0（a≠0）的两个实数根分别为3，﹣2，求一元二次方程ay2﹣（2a﹣b）y+a﹣b+c＝0的两根．（直接写出结果）
【分析】（1）根据题意，设所求方程的根是y，则y＝﹣x，所以x＝﹣y，然后把x＝﹣y代入原方程，化简可求；
（2）根据题意，设所求方程的根是y，则y＝，所以x＝，然后把x＝代入原方程，化简可求；
（3）由（2）可知，对方程cx2+bx+a＝0两边同时除以x2，得a（）2+b•+c＝0，则方程cx2+bx+a＝0的两根是ax2+bx+c＝0（a≠0）两根的倒数，进而求解．
解：（1）设所求方程的根是y，则y＝﹣x，所以x＝﹣y，
把x＝﹣y代入x2+x﹣2＝0，
得y2﹣y﹣2＝0，
故答案为：y2﹣y﹣2＝0；
（2）设所求方程的根是y，则y＝，
所以x＝，
把x＝代入方程2x2﹣7x+3＝0，得
2（）2﹣7•+3＝0，
化简，得3y2﹣7y+2＝0；
（3）一元二次方程整理后可得：a（y﹣1）2+b（y﹣1）+c＝0，
∵令y﹣1＝x，
∴y＝x+1，
则方程 a（y﹣1）2+b（y﹣1）+c＝0 的两根比 ax2+bx+c＝0（a≠0）两根大1，
所以方程 a（y﹣1）2+b（y﹣1）+c＝0 的两根分别是4、﹣1．
【点评】本题考查了一元二次方程的解，根与系数的关系，解题的关键是掌握换根法的使用．
24．将正方形ABCD的边CD绕点C顺时针旋转α°（0＜α＜90）至CP，连接PB，PD．
（1）如图1，当α＝40°时，直接写出∠BPD的大小；
（2）如图2，过点B作BE⊥PD交PD延长线于点E，连接AE．
①求∠BPD的大小；
②探究AE，PD之间的数量关系，并证明你的结论；
③当点D为PE中点时，PB＝6，直接写出四边形ABPE的面积．

【分析】（1）利用等腰三角形的性质以及三角形内角和定理求出∠CPD＝70°，∠CPB＝25°，可得结论；
（2）①作∠DCP＝α，用α表示出∠CPD，∠CPB，可得结论；
②结论：PD＝AE．过A作AF⊥AE交BE于点F．证明△ABF≌△ADE（ASA），推出BF＝DE，AF＝AE，再证明△EBP，△AEF都是等腰直角三角形，可得结论；
③分别求出△EBP，△ABE的面积，可得结论．
解：（1）如图1中，

∵四边形ABCD是正方形，
∴∠BCD＝90°，CB＝CD，
由旋转的性质可知，CD＝CP，
∵∠DCP＝40°，
∴∠CPD＝∠CDP＝（180°﹣40°）＝70°，
∵CB＝CD，CD＝CP，
∴CB＝CP，
∵∠BCP＝∠BCD+∠DCP＝130°，
∴∠CPB＝∠CBP＝（180°﹣130°）＝25°，
∴∠BPD＝∠CPD﹣∠CPB＝70°﹣25°＝45°；

（2）解：①∵CD绕顶点C顺时针旋转α°至CP，
∴CD＝CP，∠DCP＝α，
∴∠DPC＝，
∵ABCD为正方形∴BC＝CD＝CP，∠BCD＝90°，
∴∠BCP＝90+α，
∴∠BPC＝，
∴∠BPD＝∠DPC﹣∠BPC＝＝45°；

②结论：PD＝AE．
理由：过A作AF⊥AE交BE于点F．

∵ABCD为正方形，
∴AB＝AD，∠BAD＝90°，
∵AE⊥AF，
∴∠EAF＝90°，
∴∠BAD﹣∠FAD＝∠EAF﹣∠FAD，即∠BAF＝∠DAE，
又∵BE⊥PE，
∴∠BED＝90°＝∠BAD，
∴∠ABF＝∠ADE，
∴△ABF≌△ADE（ASA），
∴BF＝DE，AF＝AE，
由知∠BPD＝45°，∠BED＝90°，
∴△BEP为等腰直角三角形，
∴BE＝PE，
∴BE﹣BF＝PE﹣DE 即EF＝PD，
又∵AE＝AF，∠EAF＝90°，
∴EF＝PD＝AE；

③如图3中，

∵△PEB是等腰直角三角形，PB＝6，
∴EB＝PE＝3，
∴S△PBE＝•EB•EP＝9，
∵DE＝DP＝AE，
∴AE＝，
∵△AEF是的以及三角形，
∴∠AEB＝∠EBP＝45°，
∴AE∥PB，
∴＝＝＝，
∴S△AEB＝S△EBP＝，
∴S四边形ABPE＝S△EBP+S△AEB＝9+＝．
【点评】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．