2022-2023学年浙江省温州市龙湾区部分校七年级（下）期中数学试卷(含解析)

这是一份2022-2023学年浙江省温州市龙湾区部分校七年级（下）期中数学试卷(含解析)，共17页。试卷主要包含了如图，在所标识的角中，同位角是，运用乘法公式计算，下列式子正确的是，已知x，楠溪江某景点门票价格等内容，欢迎下载使用。
2022-2023学年浙江省温州市龙湾区部分校七年级（下）期中数学试卷
一.选择题（每题3分，本题有10小题，共30分）
1．下列各方程中，是二元一次方程的是（　　）
A． B．3x+2y＝2z C． D．3x﹣5y＝4
2．小时候我们用肥皂水吹泡泡，泡沫的厚度约为0.000326毫米，将数据0.000326用科学记数法表示为（　　）
A．0.326×10﹣3 B．32.6×10﹣5 C．3.26×10﹣4 D．3.26×10﹣3
3．如图，在所标识的角中，同位角是（　　）

A．∠1和∠2 B．∠1和∠4 C．∠2和∠4 D．∠3和∠4
4．运用乘法公式计算（2x﹣3）2结果是（　　）
A．4x2﹣9 B．2x2﹣6x+9 C．4x2﹣12x+9 D．4x2﹣6x+9
5．下列式子正确的是（　　）
A．a3+a2＝a5 B．a2•a3＝a5 C．（﹣a2）3＝a6 D．（2a2）2＝2a2
6．将方程组中的x消去后得到的方程是（　　）
A．2y＝7 B．﹣2y＝7 C．8y＝9 D．2y＝9
7．如图，AB∥CD，AD，BC相交于点O，如果∠A＝35°，∠C＝36°，那么∠COD的度数是（　　）

A．35° B．36° C．71° D．109°
8．已知x（x﹣3）＝2，那么多项式﹣2x2+6x+9的值是（　　）
A．4 B．5 C．6 D．7
9．楠溪江某景点门票价格：成人票每张70元，儿童票每张35元．小明买20张门票共花了1225元，设其中有x张成人票，y张儿童票，根据题意，下列方程组正确的是（　　）
A． B．
C． D．
10．为了求1+2+22+23+…+22022的值，可令S＝1+2+22+23+…+22022，则2S＝2+22+23+…+22023，因此2S﹣S＝22023﹣1，所以1+2+22+23+…+22022＝22023﹣1．仿照以上推理计算出1+5+52+53+…+52022的值是（　　）
A．52022﹣1 B．52023﹣1 C． D．
二、填空题（每题3分，本题有8小题，共24分）
11．已知方程5x+y＝1，改写成用含x的式子表示y的形式y＝　 　．
12．如图，如果AB∥CD，∠1＝55°，那么∠AEC＝　 　°．

13．如图，要使a∥b，需添加的一个条件是　 　（写出一个即可）

14．如图，将△ABC沿AC所在的直线平移到△DEF的位置，若图中AC＝10，DC＝3，则CF＝　 　．

15．已知方程组，则x+y的值是 　 　．
16．若x2﹣y2＝44，x﹣y＝11，则x+y＝　 　．
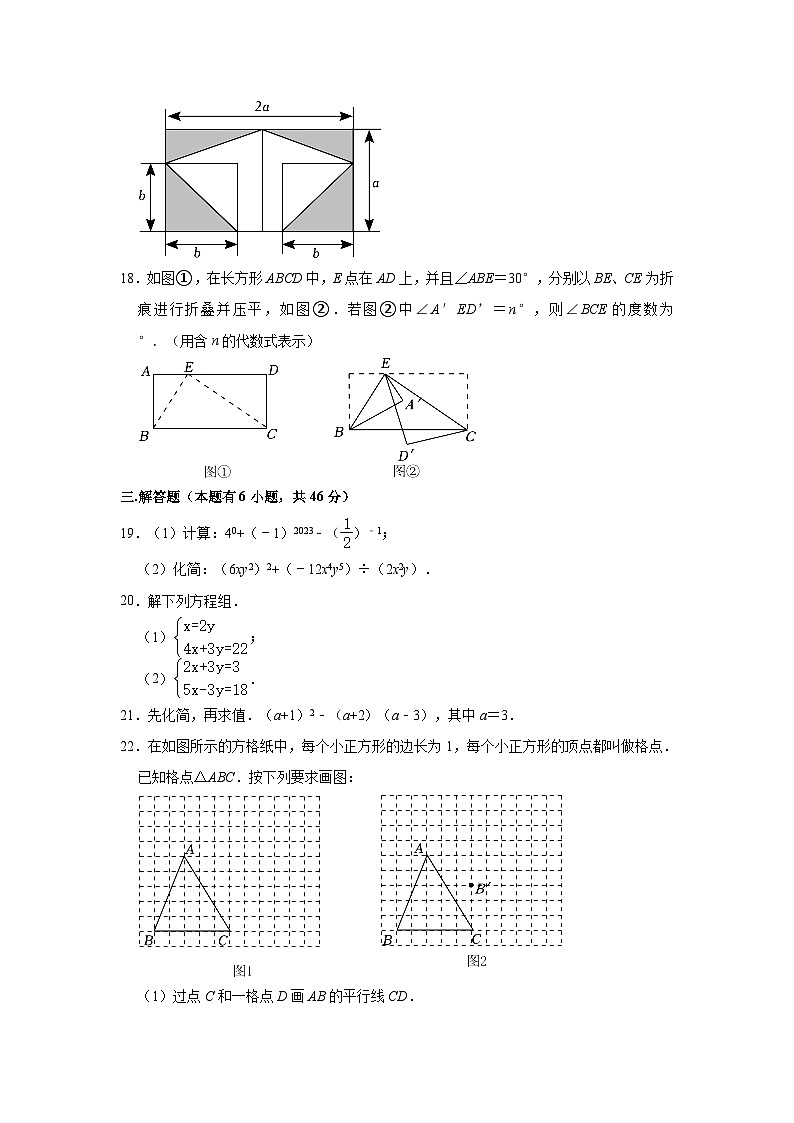
17．如图两个正方形的边长分别为a和b，若a﹣b＝3，ab＝26，那么阴影部分的面积是 　 　．

18．如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝30°，分别以BE、CE为折痕进行折叠并压平，如图②．若图②中∠A′ED’＝n°，则∠BCE的度数为 　 　°．（用含n的代数式表示）

三.解答题（本题有6小题，共46分）
19．（1）计算：40+（﹣1）2023﹣（）﹣1；
（2）化简：（6xy2）2+（﹣12x4y5）÷（2x2y）．
20．解下列方程组．
（1）；
（2）．
21．先化简，再求值．（a+1）2﹣（a+2）（a﹣3），其中a＝3．
22．在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．已知格点△ABC．按下列要求画图：

（1）过点C和一格点D画AB的平行线CD．
（2）在给定方格纸中，平移△ABC，使点B与点B′对应，请画出平移后的△A′B′C′．
23．如图，点F在线段AB上，点E，G在线段CD上，FG∥AE，∠1＝∠2．
（1）求证：AB∥CD；
（2）若FG⊥BC于点H，BC平分∠ABD，∠D＝100°，则∠1＝　 　°，∠C＝　 　°．

24．根据信息，完成活动任务：
ㅤㅤ我国是重要的农业大国，农业生产能力的提高关系到农业经济发展．在农业生产过程中，需要积极发挥新型农机具的价值，通过新型农机具的推广来扩大使用范围和应用程度，使农机具可以成为农业生产的有力助手．某农具厂需要用钢管做新型农机具骨架，按设计要求，需要使用粗细相同的长为8dm和25dm的钢管，并要求这些用料不能是焊接而成的．现钢材市场的这种规格的钢管每根为60dm．
【任务一】试问一根60dm长的钢管有哪些裁剪方法呢？请填写下空（余料作废）．
方法①：当只裁剪8dm长的用料时，最多可裁剪 　 　根；
方法②：当先裁剪下1根25dm长的用料时，余下部分最多能裁剪8dm长的用料 　 　根；
方法③：当先裁剪下2根25dm长的用料时，余下部分最多能裁剪8dm长的用料 　 　根；
【任务二】现需要长为25dm，8dm且粗细相同的钢管分别为7根，14根，分别用“任务一”中的方法②和方法③各裁剪多少根60dm长的钢管，才能刚好得到所需要的相应数量的用料？
【任务三】现设计要求更新，要用5根60dm规格的钢管裁剪出粗细相同的长为5dm的钢管18根，8dm，25dm钢管若干根，用料不能焊接，且正好裁完没有余料，则可裁剪出8dm的钢管 　 　根和25dm的钢管 　 　根．


参考答案
一.选择题（每题3分，本题有10小题，共30分）
1．下列各方程中，是二元一次方程的是（　　）
A． B．3x+2y＝2z C． D．3x﹣5y＝4
【分析】二元一次方程满足的条件：含有2个未知数，未知数的项的次数是1的整式方程．
解：A、该方程是分式方程，故此选项不合题意；
B、该方程含有三个未知数，不是二元一次方程，故此选项不合题意；
C、该方程的未知数的最高次数是2次，不是二元一次方程，故此选项不符合题意；
D、该方程是二元一次方程，故此选项合题意；
故选：D．
【点评】此题主要考查了二元一次方程的概念，要求熟悉二元一次方程的形式及其特点：含有2个未知数，未知数的项的次数是1的整式方程．
2．小时候我们用肥皂水吹泡泡，泡沫的厚度约为0.000326毫米，将数据0.000326用科学记数法表示为（　　）
A．0.326×10﹣3 B．32.6×10﹣5 C．3.26×10﹣4 D．3.26×10﹣3
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
解：0.000326＝3.26×10﹣4．
故选：C．
【点评】本题考查了科学记数法的表示方法，掌握表示形式为a×10﹣n的形式，其中1≤|a|＜10，n为整数是关键．
3．如图，在所标识的角中，同位角是（　　）

A．∠1和∠2 B．∠1和∠4 C．∠2和∠4 D．∠3和∠4
【分析】根据同位角的边呈“F”形进行分析即可．
解：A、∠1和∠2是对顶角，
故此选项不合题意；
B、∠1和∠4是同位角，
故此选项符合题意；
C、∠2和∠4是内错角，
故此选项不合题意；
D、∠3和∠4是同旁内角，
故此选项不合题意；
故选：B．
【点评】此题主要考查了同位角、内错角、同旁内角、对顶角的定义，掌握同位角、同旁内角、对顶角、内错角的定义是解题的关键．
4．运用乘法公式计算（2x﹣3）2结果是（　　）
A．4x2﹣9 B．2x2﹣6x+9 C．4x2﹣12x+9 D．4x2﹣6x+9
【分析】利用完全平方公式解答即可．
解：（2x﹣3）2＝4x2﹣12x+9，
故选：C．
【点评】本题主要考查了完全平方公式，熟练掌握完全平方公式是解题的关键．
5．下列式子正确的是（　　）
A．a3+a2＝a5 B．a2•a3＝a5 C．（﹣a2）3＝a6 D．（2a2）2＝2a2
【分析】利用合并同类项的法则，同底数幂的乘法的法则，积的乘方的法则对各项进行运算即可．
解：A、a3与a2不属于同类项，不能合并，故A不符合题意；
B、a2•a3＝a5，故B符合题意；
C、（﹣a2）3＝﹣a6，故C不符合题意；
D、（2a2）2＝4a4，故D不符合题意；
故选：B．
【点评】本题主要考查合并同类项，积的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握．
6．将方程组中的x消去后得到的方程是（　　）
A．2y＝7 B．﹣2y＝7 C．8y＝9 D．2y＝9
【分析】应用加减消元法，将方程组的两个方程的两边分别相减，判断出消去x后得到的方程即可．
解：∵（4x+5y）﹣（4x+3y）＝8﹣1＝7，
∴将方程组中的x消去后得到的方程是：2y＝7．
故选：A．
【点评】此题主要考查了解二元一次方程组的方法，注意代入消元法和加减消元法的应用．
7．如图，AB∥CD，AD，BC相交于点O，如果∠A＝35°，∠C＝36°，那么∠COD的度数是（　　）

A．35° B．36° C．71° D．109°
【分析】由AB∥CD，得到∠D＝∠A＝35°，由三角形内角和定理，即可求出∠COD的度数．
解：∵AB∥CD，
∴∠D＝∠A＝35°，
∵∠C+∠D+∠COD＝180°，∠C＝36°，
∴∠COD＝180°﹣36°﹣35°＝109°．
故选：D．
【点评】本题考查平行线的性质，三角形内角和定理，掌握平行线的性质和三角形内角和定理是解题的关键．
8．已知x（x﹣3）＝2，那么多项式﹣2x2+6x+9的值是（　　）
A．4 B．5 C．6 D．7
【分析】把所求的多项式进行整理，再代入相应的值运算即可．
解：∵x（x﹣3）＝2，
∴﹣2x2+6x+9
＝﹣2x（x﹣3）+9
＝﹣2×2+9
＝﹣4+9
＝5．
故选：B．
【点评】本题主要考查单项式乘多项式，解答的关键是对相应的运算法则的掌握．
9．楠溪江某景点门票价格：成人票每张70元，儿童票每张35元．小明买20张门票共花了1225元，设其中有x张成人票，y张儿童票，根据题意，下列方程组正确的是（　　）
A． B．
C． D．
【分析】根据“小明买20张门票”可得方程：x+y＝20；根据“成人票每张70元，儿童票每张35元，共花了1225元”可得方程：70x+35y＝1225，把两个方程组合即可．
解：设其中有x张成人票，y张儿童票，根据题意得，
，
故选：B．
【点评】此题主要考查了由实际问题抽象出二元一次方程组，关键是弄清题意，把已知量和未知量联系起来，找出题目中的相等关系．
10．为了求1+2+22+23+…+22022的值，可令S＝1+2+22+23+…+22022，则2S＝2+22+23+…+22023，因此2S﹣S＝22023﹣1，所以1+2+22+23+…+22022＝22023﹣1．仿照以上推理计算出1+5+52+53+…+52022的值是（　　）
A．52022﹣1 B．52023﹣1 C． D．
【分析】本题通过题干给出的方法，可以设M＝1+5+52+53+…+52022，然后用5M﹣M，得到M的解．
解：设M＝1+5+52+53+…+52022，
5M＝5+52+53+54+…+52023，
5M﹣M＝5+52+53+54+…+52023﹣（1+5+52+53+…+52022），
4M＝52023﹣1，
M＝，
故选：D．
【点评】本题考查有理数的混合运算，和基于题干给出的方法来进行类似的运算．
二、填空题（每题3分，本题有8小题，共24分）
11．已知方程5x+y＝1，改写成用含x的式子表示y的形式y＝　1﹣5x　．
【分析】根据等式的性质移项即可．
解：5x+y＝1，
y＝1﹣5x．
故答案为：1﹣5x．
【点评】本题考查解二元一次方程，解题关键是熟知移项的计算过程．
12．如图，如果AB∥CD，∠1＝55°，那么∠AEC＝　55　°．

【分析】由AB∥CD，即可得到∠AEC＝∠1＝55°．
解：∵AB∥CD，
∴∠AEC＝∠1＝55°．
故答案为：55．
【点评】本题考查平行线的性质，关键是掌握平行线的性质：两直线平行，内错角相等．
13．如图，要使a∥b，需添加的一个条件是　∠1＝∠4　（写出一个即可）

【分析】根据同位角相等两直线平行，图中∠1和∠4为同位角，所以加上∠1＝∠4即可．
解：∵图中∠1和∠4 为同位角，
根据同位角相等两直线平行，则加上∠1＝∠4，可得a∥b．
【点评】本题比较简单，记住平行线的判定定理即可．
14．如图，将△ABC沿AC所在的直线平移到△DEF的位置，若图中AC＝10，DC＝3，则CF＝　7　．

【分析】根据平移的性质即可得到结论．
解：∵将△ABC沿AC所在的直线平移到△DEF，
∴DF＝AC＝10，
∵DC＝3，
∴CF＝DF﹣CD＝10﹣3＝7，
故答案为：7．
【点评】本题考查了平移的性质，熟练掌握平移的性质是解题的关键．
15．已知方程组，则x+y的值是 　3　．
【分析】两方程相加即可得到3x+3y＝9，即可求得x+y＝3．
解：，
①+②得：3x+3y＝9，
∴x+y＝3．
故答案为：3．
【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
16．若x2﹣y2＝44，x﹣y＝11，则x+y＝　4　．
【分析】把x2﹣y2＝（x+y）（x﹣y）利用平方差公式展开，然后把x2﹣y2＝44，x﹣y＝11代入计算整理即可求解．
解：因为x2﹣y2＝（x+y）（x﹣y），
所以x+y＝（x2﹣y2）÷（x﹣y）＝44÷11＝4；
故答案为：4．
【点评】本题考查了平方差公式的应用，把已知条件x2﹣y2＝（x+y）（x﹣y）变形是解题的关键．
17．如图两个正方形的边长分别为a和b，若a﹣b＝3，ab＝26，那么阴影部分的面积是 　35　．

【分析】按照三角形的面积公式表示出阴影面积后，将结果配成完全平方式的形式，再代入已知值即可．
解：有图得，整个图形面积为：2a•a＝2a2，
上面两个阴影图形面积相等，面积之和为：2•a（a﹣b）＝a2﹣ab，
下面两个阴影图形面积相等，面积之和为：2•b2＝b2，
∴阴影面积：a2﹣ab+b2
＝（a﹣b）2+ab，
∵a﹣b＝3，ab＝26，
∴原式＝32+26
＝9+26
＝35．
故答案为：35．
【点评】本题考查了完全平方式的应用，准确求出面积并配成完全平方式是解题关键．
18．如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝30°，分别以BE、CE为折痕进行折叠并压平，如图②．若图②中∠A′ED’＝n°，则∠BCE的度数为 　（30+n）　°．（用含n的代数式表示）

【分析】根据折叠求出∠AEA′＝120°，再表示出∠AED′＝120﹣n°，表示出∠DED′＝60°+n°，根据折叠求出∠DEC＝∠DED′，再根据平行求出答案即可．
解：∵∠ABE＝30°，
∴∠AEB＝60°，
∴∠AEA′＝120°，
∴∠A′ED’＝n°，
∴∠AED′＝120﹣n°，
∴∠DED′＝180°﹣（120﹣n°）＝60°+n°，
由折叠得∠DEC＝（60°+n°）＝30°+n°，
∵AD∥BC，
∴∠BCE＝∠DEC＝30°+n°．
故答案为：（30+n）．
【点评】本题考查了角度的求解，熟练运用矩形形状和折叠性质是解题关键．
三.解答题（本题有6小题，共46分）
19．（1）计算：40+（﹣1）2023﹣（）﹣1；
（2）化简：（6xy2）2+（﹣12x4y5）÷（2x2y）．
【分析】（1）直接利用负整数指数幂的性质以及零指数幂的性质、有理数的乘方运算法则分别化简，进而得出答案；
（2）直接利用积的乘方运算法则化简，再利用整式的除法运算法则计算得出答案．
解：（1）原式＝1﹣1﹣2
＝﹣2；

（2）原式＝36x2y4﹣6x2y4
＝30x2y4．
【点评】此题主要考查了实数的运算以及整式的除法运算，正确掌握相关运算法则是解题关键．
20．解下列方程组．
（1）；
（2）．
【分析】（1）利用代入消元法解方程即可；
（2）利用加减消元法解方程即可．
解：（1），
把①代入②得：8y+3y＝22，
解得：y＝2，
把y＝2代入①中得：x＝4，
∴原方程组的解为；
（2），
由①+②得：7x＝21，
解得：x＝3，
把x＝3代入①得：6+3y＝3，
解得：y＝﹣1，
∴原方程组的解为．
【点评】本题主要考查二元一次方程组的解法，掌握代入消元法和加减消元法解方程是解题的关键．
21．先化简，再求值．（a+1）2﹣（a+2）（a﹣3），其中a＝3．
【分析】根据完全平方公式、多项式乘多项式将题目中的式子展开，然后合并同类项，再将a的值代入化简后的式子计算即可．
解：（a+1）2﹣（a+2）（a﹣3）
＝a2+2a+1﹣（a2﹣a﹣6）
＝a2+2a+1﹣a2+a+6
＝3a+7，
当a＝3时，原式＝3×3+7＝16．
【点评】本题考查整式的混合运算—化简求值，熟练掌握运算法则是解答本题的关键，注意完全平方公式的应用．
22．在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．已知格点△ABC．按下列要求画图：

（1）过点C和一格点D画AB的平行线CD．
（2）在给定方格纸中，平移△ABC，使点B与点B′对应，请画出平移后的△A′B′C′．
【分析】（1）根据网格特点及平行线的判定作图即可；
（2）将点A、C分别向右平移5个单位，向上平移3个单位得到其对应点，再首尾顺次连接即可．
解：（1）如图所示，直线CD即为所求．

（2）如图所示，△A′B′C′即为所求．
【点评】本题主要考查作图—平移变换，解题的关键是掌握平移变换的定义与性质，并据此得出变换后的对应点．
23．如图，点F在线段AB上，点E，G在线段CD上，FG∥AE，∠1＝∠2．
（1）求证：AB∥CD；
（2）若FG⊥BC于点H，BC平分∠ABD，∠D＝100°，则∠1＝　50　°，∠C＝　40　°．

【分析】（1）欲证明AB∥CD，只要证明∠1＝∠HGC即可；
（2）根据平行线的性质得∠ABD+∠D＝180°，∠C＝∠FBC，根据角平分线的定义得∠FBC＝∠ABD＝40°，所以∠C＝∠FBC，根据∠1+∠FBC＝90°，即可求出∠1．
【解答】（1）证明：∵FG∥AE，
∴∠2＝∠HGC，
∵∠1＝∠2，
∴∠1＝∠HGC，
∴AB∥CD；
（2）解：∵AB∥CD，
∴∠ABD+∠D＝180°，∠C＝∠FBC，
∵∠D＝100°，
∴∠ABD＝180°﹣∠D＝80°，
∵BC平分∠ABD，
∴∠FBC＝∠ABD＝40°，
∴∠C＝∠FBC＝40°，
∵FG⊥BC，
∴∠1+∠FBC＝90°，
∴∠1＝90°﹣40°＝50°，
故答案为：50，40．
【点评】本题考查了平行线的性质，角平分线的定义等知识，熟练掌握基本知识是解题的关键．
24．根据信息，完成活动任务：
ㅤㅤ我国是重要的农业大国，农业生产能力的提高关系到农业经济发展．在农业生产过程中，需要积极发挥新型农机具的价值，通过新型农机具的推广来扩大使用范围和应用程度，使农机具可以成为农业生产的有力助手．某农具厂需要用钢管做新型农机具骨架，按设计要求，需要使用粗细相同的长为8dm和25dm的钢管，并要求这些用料不能是焊接而成的．现钢材市场的这种规格的钢管每根为60dm．
【任务一】试问一根60dm长的钢管有哪些裁剪方法呢？请填写下空（余料作废）．
方法①：当只裁剪8dm长的用料时，最多可裁剪 　7　根；
方法②：当先裁剪下1根25dm长的用料时，余下部分最多能裁剪8dm长的用料 　4　根；
方法③：当先裁剪下2根25dm长的用料时，余下部分最多能裁剪8dm长的用料 　1　根；
【任务二】现需要长为25dm，8dm且粗细相同的钢管分别为7根，14根，分别用“任务一”中的方法②和方法③各裁剪多少根60dm长的钢管，才能刚好得到所需要的相应数量的用料？
【任务三】现设计要求更新，要用5根60dm规格的钢管裁剪出粗细相同的长为5dm的钢管18根，8dm，25dm钢管若干根，用料不能焊接，且正好裁完没有余料，则可裁剪出8dm的钢管 　20　根和25dm的钢管 　2　根．
【分析】【任务一】利用算术方法直接解答即可；
【任务二】设未知数，再利用“需要长为25dm，8dm且粗细相同的钢管分别为7根，14根”列出二元一次方程组，解出即可；
【任务三】设未知数，利用“5dm的钢管18根，8dm，25dm钢管若干根”列二元一次方程，再求其整数解即可．
解：【任务一】
方法①：60÷8＝7……4，
∴当只裁剪8dm长的用料时，最多可裁剪7根，
方法②：（60﹣25）÷8＝4……3，
∴当先裁剪下1根25dm长的用料时，余下部分最多能裁剪8dm长的用料4根，
方法③：（60﹣25×2）÷8＝1……2，
∴当先裁剪下2根25dm长的用料时，余下部分最多能裁剪8dm长的用料1根，
故答案为：7，4，1；
【任务二】设分别用“任务一”中的方法②和方法③各裁剪x根和y根60dm长的钢管，
根据题意，得
解得
答：分别用“任务一”中的方法②和方法③各裁剪3根和2根60dm长的钢管；
【任务三】设可裁剪出8dm的钢管a根，25dm的钢管b根，
根据题意，得8a+25b+5×18＝60×5，
整理，得b＝，
即b＝8+，
∵a，b均为整数，
∴
∴可裁剪出8dm的钢管20根，25dm的钢管2根，
故答案为：20，2．
【点评】本题考查二元一次方程组的应用，二元一次方程整数解的应用，解题的关键是弄清题意，发现其中的等量关系列出方程（组）．