2023年四川省攀枝花市中考二模数学试题（含答案）

这是一份2023年四川省攀枝花市中考二模数学试题（含答案），共19页。试卷主要包含了填空题．，解答题等内容，欢迎下载使用。

2023年春季学期4月九年级联考
数学试题
一、选择题（每小题5分，共60分）下列各小题均有四个答案，其中只有一个是正确的．
1．在，，，这四个数中，最大的数是（ ）
A． B． C． D．
2．在如图所示的几何体中，主视图和俯视图相同的是（ ）
A．正方体 B．三棱柱 C．圆柱 D．圆锥
3．下列计算正确的是（ ）
A． B． C． D．
4．碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.5纳米的碳纳米管，1纳米＝0.000000001米，则0.5纳米用科学记数法表示为（ ）
A．米 B．米 C．米 D．米
5．下列说法正确的是（ ）
A．为了解春节期间河南省的空气质量，采用全面调查
B．射击运动员射击一次，命中靶心为必然事件
C．数据2，2，2，2，2的方差为0
D．数据6，8，6，13，8，12的众数为8
6．两个直角三角板如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AB与DF交于点M．若，则∠BMD的大小为（ ）

A．60° B．75° C．67.5° D．82.5°
7．若关于x的方程的解是正数，则m的取值范围为（ ）
A．m＞－7 B．m＞－7且 C．m＜－7 D．m＞－7且
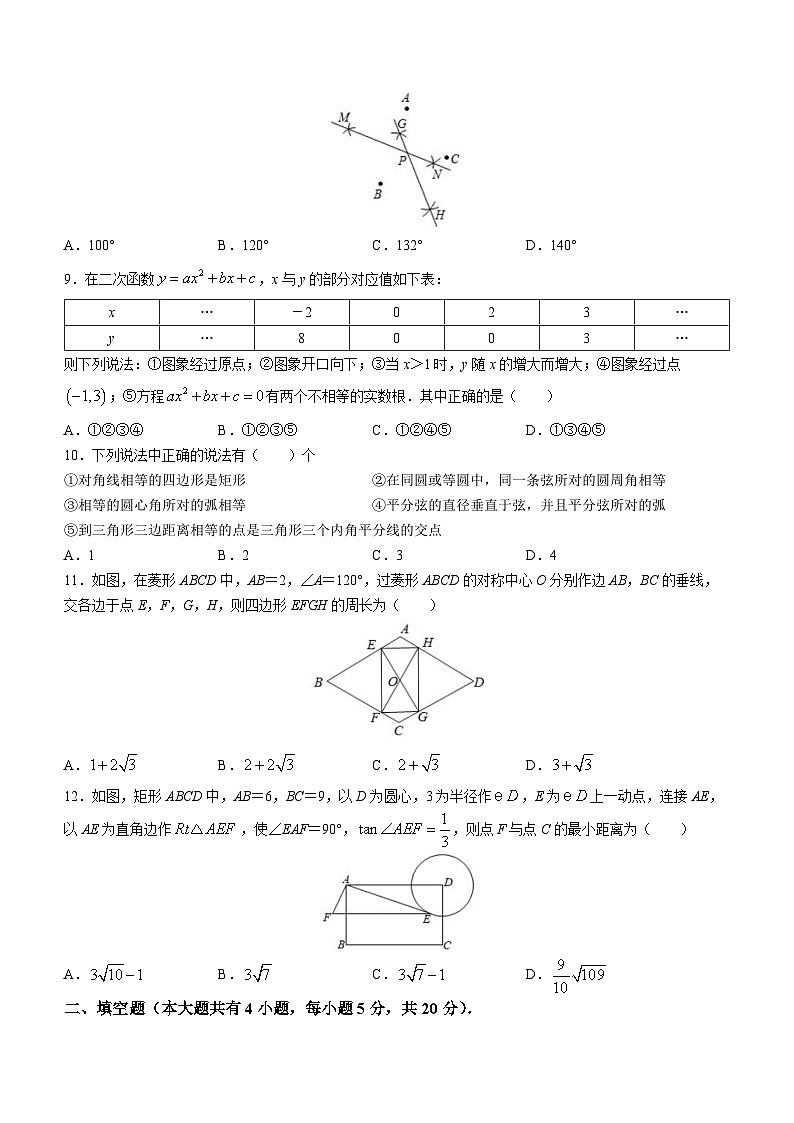
8．如图所示的是A、B、C三点，按如下步骤作图：①先分别以A、B两点为圆心，以大于的长为半径作弧，两弧相交于M、N两点，作直线MN；②再分别以B、C两点为圆心，以大于的长为半径作弧，两弧相交于G、H两点，作直线GH，GH与MN交于点P，若∠BAC＝66°，则∠BPC等于（ ）

A．100° B．120° C．132° D．140°
9．在二次函数，x与y的部分对应值如下表：
x
…
－2
0
2
3
…
y
…
8
0
0
3
…
则下列说法：①图象经过原点；②图象开口向下；③当x＞1时，y随x的增大而增大；④图象经过点；⑤方程有两个不相等的实数根．其中正确的是（ ）
A．①②③④ B．①②③⑤ C．①②④⑤ D．①③④⑤
10．下列说法中正确的说法有（ ）个
①对角线相等的四边形是矩形 ②在同圆或等圆中，同一条弦所对的圆周角相等
③相等的圆心角所对的弧相等 ④平分弦的直径垂直于弦，并且平分弦所对的弧
⑤到三角形三边距离相等的点是三角形三个内角平分线的交点
A．1 B．2 C．3 D．4
11．如图，在菱形ABCD中，AB＝2，∠A＝120°，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H，则四边形EFGH的周长为（ ）

A． B． C． D．
12．如图，矩形ABCD中，AB＝6，BC＝9，以D为圆心，3为半径作，E为上一动点，连接AE，以AE为直角边作，使∠EAF＝90°，，则点F与点C的最小距离为（ ）

A． B． C． D．
二、填空题（本大题共有4小题，每小题5分，共20分）．
13．因式分解：______．
14．如图，在正方形ABCD中，E为AD的中点，连接BE交AC于点F．若AB＝6，则的面积为______．

15．已知关于x的一元二次方程有两个不相等的实数根，则m的取值范围是______．
16．如图，四边形ABCD是正方形，点E在CB的延长线上，连接AE，交CD于点F，连接EF，点H是EF的中点，连接BH，则下列结论中：①BE＝DF；②∠BEH＝∠BAH；③；④若AB＝4，DF＝1，则的面积为．正确的是______（填写所有正确结论的序号）．

三、解答题（共70分）
17．计算（8分）

18．（8分）将两个全等的直角三角形按如图所示摆放，使点A、E、D在同一条直线上．利用此图的面积表示式证明勾股定理．

19．（8分）为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：

（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．
20．（8分）图（1）为某大型商场的自动扶梯、图（2）中的AB为从一楼到二楼的扶梯的侧面示意图．小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（）向正前方走了2m，发现日光灯C刚好在他的正上方．已知自动扶梯AB的坡度为，AB的长度是13m．（参考数据：，，）

（1）求图中B到一楼地面的高度．
（2）求日光灯C到一楼地面的高度．（结果精确到十分位）
21．（8分）如图，在平面直角坐标系xOy中，一次函数y＝x＋b的图象经过点，与反比例函数的图象交于点和点C．

（1）求一次函数和反比例函数的表达式；
（2）若点P在y轴上，且的面积等于6，求点P的坐标．
22．（8分）如图，已知AB，CD为的直径，过点A作弦AE垂直于直径CD于点F，点B恰好为的中点，连接BC，BE．

（1）求证：AE＝BC；
（2）若，求的半径．
23．（10分）抛物线与x轴交于，两点，与y轴交于点C，直线y＝kx－6经过点B．点P在抛物线上，设点P的横坐标为m．

（1）求抛物线的表达式和t，k的值；
（2）如图1，连接AC，AP，PC，若是以CP为斜边的直角三角形，求点P的坐标；
（3）如图2，若点P在直线BC上方的抛物线上，过点P作，垂足为Q，求的最大值．
24．（12分）如图，在中，∠A＝90°，AB＝6cm，AC＝8cm，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向以1cm/s的速度运动，过点P作于Q，过点Q作交AC于R，交DE于G，当点Q与点C重合时，点P停止运动．设点P运动时间为．

（1）点D到BC的距离DH的长是______；
（2）令QR＝y，求y关于t的函数关系式（不要求写出自变量的取值范围）；
（3）是否存在点P，使为等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由．

2023年春季学期4月九年级联考
数学试题
一、选择题（每小题5分，共600分）下列各小题均有四个答案，其中只有一个是正确的．
1．【答案】C
【分析】比较四个数的大小关系，即可得出结论．
【详解】解：，，，，
∴，
故选C．
【点睛】本题考查比较实数的大小．熟练掌握比较实大小的方法，是解题的关键．
2．【答案】A
【分析】根据主视图和俯视图分别是从物体正面和上面看到的图形，进而判断即可．
【详解】正方体的主视图和俯视图都是正方形，其主视图和俯视图相同，故A选项符合题意；
三棱柱的主视图是长方形，俯视图是三角形，其主视图和俯视图不同，故B选项不符合题意；
圆柱的主视图是长方形，俯视图是圆，其主视图和俯视图不同，故C选项不符合题意；
圆锥的主视图是三角形，俯视图是圆（圆心标出），其主视图和俯视图不同，故D选项不符合题意；
故选：A．
【点睛】本题考查了简单几何体的三视图，掌握主视图，左视图和俯视图分别是从物体的正面，左面和上面看是解题的关键．
3．【答案】C
【解析】
【分析】根据算术平方根，单项式的除法，积的乘方，完全平方公式逐项分析判断即可．
【详解】解：A．，故该选项不正确，不符合题意；
B．，故该选项不正确，不符合题意；
C．，故该选项正确，符合题意；
D．，故该选项不正确，不符合题意．
故选：C
【点睛】本题考查了算术平方根，单项式的除法，积的乘方，完全平方公式，正确的计算是解题的关键．
4．【答案】B
【分析】纳米米．小于1的正数也可以利用科学记数法表示，一般形式为，，n为第一位有效数字前面0的个数，在本题中a为5，n为．
【详解】解：纳米米米，故选：B．
【点睛】此题主要考查了用科学记数法表示较小的数；一般形式为，，确定a与n的值是解题的关键．
5．【答案】C
【分析】A、根据全面调查与抽样调查的概念解答即可；B、根据必然事件的意义解答即可；C、根据方差的概念解答即可；D、根据众数的定义解答即可．
【详解】解：A、为了解春节期间河南省的空气质量，采用抽样调查，故不合题意；
B、射击运动员射击一次，命中靶心为随机事件，故不合题意；
C、数据2，2，2，2，2的方差为，故符合题意；
D、数据6，8，6，13，8，12的众数为6和8，故不合题意；
故选：C．
【点睛】此题考查的是随机事件，全面调查与抽样调查，众数与方差的概念，掌握其定义是解决此题的关键．
6．【答案】B
【解析】
【分析】根据，可得再根据三角形内角和即可得出答案．
【详解】由图可得
∵，
∴
∴
故选：B．
【点睛】本题考查了平行线的性质和三角形的内角和，掌握平行线的性质和三角形的内角和是解题的关键．
7．【考点】分式方程的解；解一元一次不等式．
【专题】分式方程及应用；运算能力．
【分析】先解分式方程，得．再根据分式方程的解的定义解决此题．
【解答】解：，
去分母，得2x＋m－x＋1＝3（x－2）．
去括号，得2x＋m－x＋1＝3x－6．
移项，得2x－x－3x＝－6－1－m．
合并同类项，得－2x＝－7－m．
x的系数化为1，得．
∵关于x的方程的解是正数，
∴且．
∴m＞－7且m≠－3．
故选：B．
【点评】本题主要考查分式方程的解，熟练掌握分式方程的解的定义、解一元一次不等式是解决本题的关键．
8．【答案】C
【解析】
【分析】根据基本作图可判断MN垂直平分AB，GH垂直平分BC，根据垂直平分线的性质可得，再利用等腰三角形的性质得到，，最后根据三角形的外角性质可得∠BPC＝2∠BAC，据此求解即可．
【详解】解:如图，连接、、、、、，

由作法可知垂直平分，垂直平分，
∴，
∴，，
∴，
∴，
∴．
故选：C．
【点睛】本题考查了线段垂直平分线的基本作图及线段垂直平分线的性质，利用等腰三角形的性质，三角形的外角性质．
9．【答案】D
【分析】结合图表可以得出当或2时，；时，，根据待定系数法可求出二次函数解析式，从而根据二次函数的性质判断．
【详解】解：∵由图表可以得出当或2时，；时，，
∴，解得：，∴，
∵，∴图象经过原点，故①正确；
∵，∴抛物线开口向上，故②错误；
∵抛物线的对称轴是，
∴时，y随x的增大而增大，故③正确；
把代入得，，∴图象经过点，故④正确；
∵抛物线与x轴有两个交点、，
∴有两个不相等的实数根，故⑤正确；
综上，正确的有①③④⑤．
故选：D．
【点睛】此题主要考查了待定系数法求二次函数解析式，熟知二次函数的性质是解题的关键．
10．答案A
11．【答案】D
【解析】
【分析】依次求出OE＝OF＝OG＝OH，利用勾股定理得出EF和OE的长，即可求出该四边形的周长．
【详解】∵HF⊥BC，EG⊥AB，
∴∠BEO＝∠BFO＝90°，
∵∠A＝120°，
∴∠B＝60°，
∴∠EOF＝120°，∠EOH＝60°，
由菱形的对边平行，得HF⊥AD，EG⊥CD，
因为O点是菱形ABCD的对称中心，
∴O点到各边的距离相等，即OE＝OF＝OG＝OH，
∴∠OEF＝∠OFE＝30°，∠OEH＝∠OHE＝60°，
∴∠HEF＝∠EFG＝∠FGH＝∠EHG＝90°，
所以四边形EFGH是矩形；
设OE＝OF＝OG＝OH＝x，
∴EG＝HF＝2x，，
如图，连接AC，则AC经过点O，
可得三角形ABC是等边三角形，
∴∠BAC＝60°，AC＝AB＝2，∴OA＝1，∠AOE＝30°，
∴AE＝，∴x＝OE＝
∴四边形EFGH的周长为EF＋FG＋GH＋HE＝，故选D．

【点睛】本题考查了菱形的性质、矩形的判定与性质、等边三角形的判定与性质、勾股定理．
12．【答案】A
【详解】如图，取的中点，连接．．．

，，，
，，，
，，，
四边形是矩形，，
，，，
，，点的运动轨迹是以为圆心1为半径的圆，
，，
，的最小值为．
二、填空题（本大题共有 4小题，每小题5分，共20分）．
13．【答案】
【分析】根据提公因式因式分解即可求解．
【详解】解：，
故答案为：．
14．【答案】3
【分析】由正方形的性质可知，则可判断，利用相似三角形的性质得到，然后根据三角形面积公式得到．
【详解】解：∵四边形是正方形，
∴，
∵E为的中点，∴，
∵，∴，∴，
15．【答案】且m≠0
【解析】
【分析】由二次项系数非零结合根的判别式，即可得出关于m的一元一次不等式组，解之即可得出结论．
【详解】解：∵关于x的一元二次方程mx2-4x＋2＝0有两个不相等的实数根，
∴，解得：且m≠0故答案为：且m≠0．
【点睛】本题主要考查根的判别式，一元二次方程ax2＋bx＋c＝0（a≠0）的根与有如下关系：
①当时，方程有两个不相等的两个实数根；
②当时，方程有两个相等的两个实数根；
③当时，方程无实数根．
16．【答案】①②③
【分析】证明△ABE≌△ADF（ASA），可判断①；利用等腰三角形三线合一性质证明AH⊥EF，可得∠ABE＝∠AHE＝90°，最后得出结论即可判断②；在BC上截取CG＝CF，连接FG，利用等腰直角三角形性质及中位线定理进行判断③；过点H作HM⊥BC，可得HM＝FC，最后求得的面积进行判断④．
【详解】解：∵四边形ABCD是正方形，
∴AB＝AD，∠ABC＝∠ABE＝∠ADF＝∠BAD＝90°，
∵AE⊥AF，∴∠EAF＝∠BAD＝90°，∴∠BAE＝∠DAF，
∴△AEE≌△ADF（ASA），∴BE＝DF，故①正确；
∵△AEE≌△ADF，∴AE＝AF，
设AB与EH相交于点O，则∠BOE＝∠AOH，

∵点H是的中点，∴AH⊥EF，∴∠ABE＝∠AHE＝90°，
∴，故②正确；
如图，在BC上截取CG＝CF，连接FG，

∵∠C＝90°，∴△CGF是等腰直角三角形，∴，
∵BC＝DC，CG＝CF，∴DF＝BG，
∵DF＝BE，∴BG＝BE，∵EH＝HF，∴BH＝GF，
∴，故③正确；
如图，过点H作HM⊥BC，

∵，∴CF＝3，BE＝1，
∵EH＝HF，HM⊥BC，FC⊥BC，∴HM＝FC＝，
∴，故④错误；
∴正确的有①②③共3个，
故答案为 ①②③．
【点睛】本题考查正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考选择题中的压轴题．
17．答案
18．【分析】先推出△BEC是直角三角形，然后根据S梯形ABCD＝S△ABE＋S△BEC＋S△DEC，代入字母整理化简，即可证明结论成立．
【解答】证明：由已知可得，Rt△BAE≌Rt△EDC，
∴∠ABE＝∠DEC，∵∠ABE＋∠AEB＝90°，∴∠DEC＋∠AEB＝90°，
∴∠BEC＝90°，∴△BEC是直角三角形，∴S梯形ABCD＝S△ABE＋S△BEC＋S△DEC，
∴，∴，∴a2＋b2＝c2．
【点评】本题考查勾股定理的证明，解答本题的关键是推出△BEC是直角三角形．
19．【分析】（1）用A的人数除以所占的百分比，即可求出调查的学生数；
（2）用抽查的总人数减去A、C、D的人数，求出喜欢“立定跳远”的学生人数，再除以被调查的学生数，求出所占的百分比，再画图即可；
（3）用A表示男生，B表示女生，画出树形图，再根据概率公式进行计算即可．
【解答】解：（1）根据题意得：15÷10%＝150（名）．
答；在这项调查中，共调查了150名学生；
（2）本项调查中喜欢“立定跳远”的学生人数是；150－15－60－30＝45（人），
所占百分比是：×100%＝30%，画图如下：

（3）用A表示男生，B表示女生，画图如下：

共有20种情况，同性别学生的情况是8种，则刚好抽到同性别学生的概率是．
【点评】本题考查的是条形统计图和扇形统计图的综合运用以及概率的求法，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
20．【考点】解直角三角形的应用－仰角俯角问题；解直角三角形的应用－坡度坡角问题．
【专题】解直角三角形及其应用；运算能力；推理能力；应用意识．
【答案】（1）5m； （2）约为12.3m．
【分析】（1）过点B作BE⊥MN于E，由坡度的定义和勾股定理求解即可；
（2）过点C作CF⊥MN于F交BL于G，过点D作DJ⊥CF于J交BE于H，则四边形BEFG、四边形ADJF是矩形，求出AF＝DJ＝14m，再由三角函数定义求出CJ＝10.5m，即可得出结果．
【解答】解：（1）过点B作BE⊥MN于E，如图（2）所示：
设AE＝xm，∵AB的坡度为1：2.4，
∴，∴，
在Rt△ABE中，由勾股定理得：，
解得：x＝12，∴AE＝12m，BE＝5m，
答：B到一楼地面的高度为5m；
（2）过点C作CF⊥MN于F交BL于G，过点D作DJ⊥CF于J交BE于H，
则BG＝2m，四边形BEFG、四边形ADJF是矩形，∠CDJ＝37°，
∴EF＝BG＝2m，AD＝FJ＝1.8m，AF＝DJ，
由（1）可知，AF＝AE＋EF＝12＋2＝14（m），
∴DJ＝14m，
在Rt△CDJ中，，
∴CJ≈0.75DJ＝0.75×14＝10.5（m），
∴CF＝CJ＋FJ＝10.5＋1.8＝12.3（m），
答：日光灯C到一楼地面的高度约为12.3m．

【点评】本题考查了解直角三角形的应用－仰角俯角问题、解直角三角形的应用－坡度坡角问题，正确作出辅助线构造直角三角形是解题的关键．
21．【分析】（1）利用待定系数法可求解析式；
（2）联立方程组可求点C坐标，利用三角形的面积公式可求解；
【解答】解：（1）∵一次函数y＝x＋b的图象经过点A（－2，0），
∴b＝2，∴直线解析式为y＝x＋2，
∵点B（a，4）在直线y＝x＋2上，
∴4＝a＋2，∴a＝2，∴点B（2，4），
∵反比例函数的图象过点B（2，4），∴k＝2×4＝8，
∴反比例函数解析式为；
（2）如图1，设直线AB与y轴交于点D，点P坐标为（0，p），

∵直线AB与y轴交于点D，∴点D（0，2），
联立方程得：，解得：，或，
∴，∴，
∴p＝0或4，∴P（0，0）或（0，4）．
22．【答案】（1）证明见详解； （2）2；
【解析】【分析】（1）连接 ，，为的直径，得到两个直角及两条线段相等，再根据弧的中点得到弧相等，从而等到角相等，证明两个三角形全等即可得到答案；
（2）连接，根据弧的中点得到弧相等，从而等到圆周角圆心角的关系，结合平角，求出的度数，在中根据勾股定理即可得到答案；
证明：连接 ，

∵，为的直径，∴，，
∵点B是 的中点，∴，∴，
在与中，∵，，，
∴≌，∴；
【小问2详解】
解：连接，

∵点B是的中点，∴，
∴，，
∵垂直于直径于F，，
∴，，，
∵，∴，
∵，∴，
∴，∴，
在中，，解得：；
【点睛】本题考查了垂径定理、圆周角定理、扇形的面积以及解直角三角形等，作出辅助线构建直角三角形和等边三角形是解题的关键．
23．【分析】（1）用待定系数法求函数的解析式即可求解；
（2）作PM⊥x轴交于M，可求，，通过证明△COA∽△AMP，利用，求m的值即可求P点坐标；
（3）作PN⊥x轴交BC于N，过点N作NE⊥y轴交于E，通过证明△PQN∽△BOC，求出，，再由△CNE∽△CBO，求出，则，即可求解．
【解答】解：（1）将B（8，0）代入，
∴64a＋22－6＝0，∴，∴，
当y＝0时，，解得t＝3或t＝8（舍），∴t＝3，
∵B（8，0）在直线y＝kx－6上，∴8k－6＝0，解得；
（2）作PM⊥x轴交于M，∵P点横坐标为m，
∴，∴，AM＝m－3，
在Rt△COA和Rt△AMP中，∵∠OAC＋∠PAM＝90°，∠APM＋∠PAM＝90°，
∴∠OAC＝∠APM，∴△COA∽△AMP，∴，即OA•MA＝CO•PM，
，解得m＝3（舍）或m＝10，∴；
（3）作PN⊥x轴交BC于N，过点N作NE⊥y轴交于E，
∴，
∵PN⊥x轴，∴，∴∠PNQ＝∠OCB，
∴Rt△PQN∽Rt△BOC，∴，
∵OB＝8，OC＝6，BC＝10，∴，，
由，∴，
∴，
∴，
当时，的最大值是．

【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，三角形相似的判定及性质是解题的关键．
24.【解答】解：（1）在Rt△ABC中，∵∠A＝90°，AB＝6，AC＝8，
∴．∵∠DHB＝∠A＝90°，∠B＝∠B．
∴△BHD∽△BAC，∴，
∴；故答案为：；
（2）∵QR∥AB，∴∠QRC＝∠A＝90°．
∵∠C＝∠C，∴△RQC∽△ABC，∴，
∵，∴，
∴，即y关于x的函数关系式为：；
（3）存在，分三种情况：
①如图2当PQ＝PR时，过点P作PM⊥QR于M，则QM＝RM．
∵∠1＋∠2＝90°，∠C＋∠2＝90°，∴∠1＝∠C．
∴，∴，
∴，∴．
②如图3，当PQ＝RQ时，，∴．
③如图4，作EM⊥BC，RN⊥EM，∴EM∥PQ，
当PR＝QR时，则R为PQ中垂线上的点，∴EN＝MN，∴ER＝RC，
∴点R为EC的中点，∴．
∵，∴，∴t＝5.7．
综上所述，当t为或或5.7时，△PQR为等腰三角形．

【点评】本题考查了相似三角形的判定和性质，锐角三角函数，等腰三角形的性质，解答此题的关键是根据题意画出图形，用数形结合的方法解答．