初中数学3.5 探索与表达规律教案设计

这是一份初中数学3.5 探索与表达规律教案设计，共9页。教案主要包含了教学目标，教学重难点，教学用具，教学过程设计等内容，欢迎下载使用。
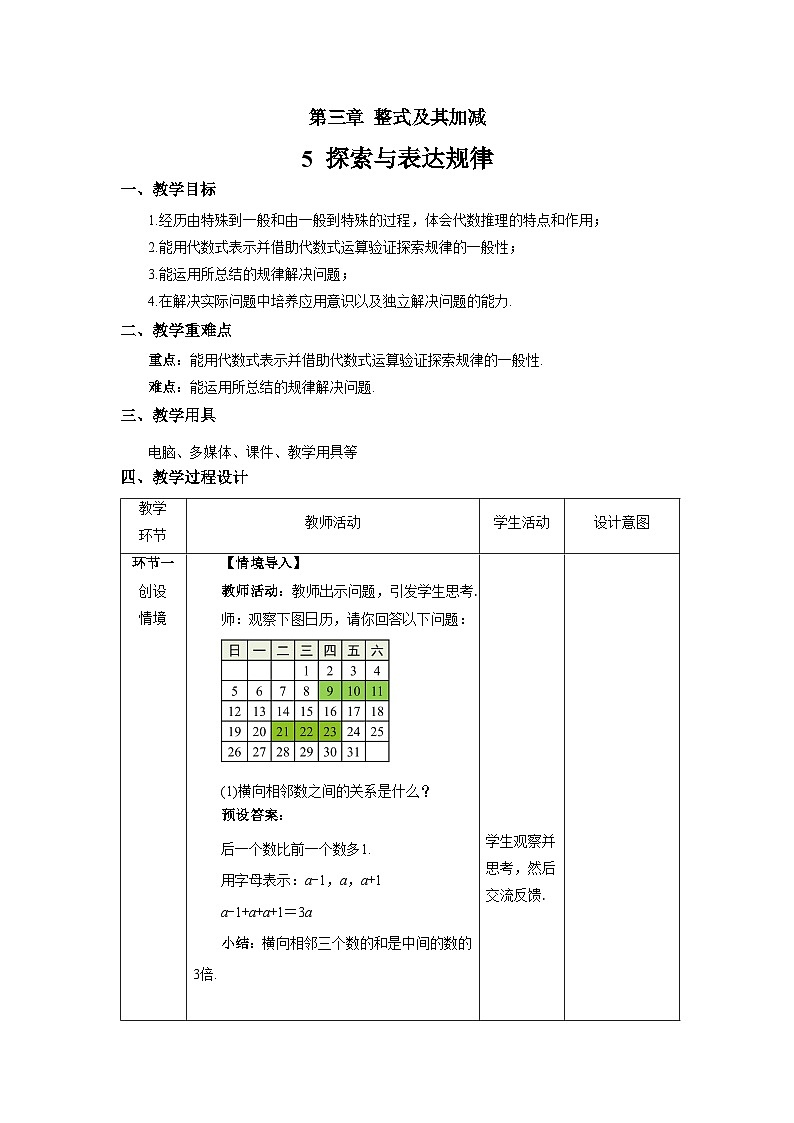
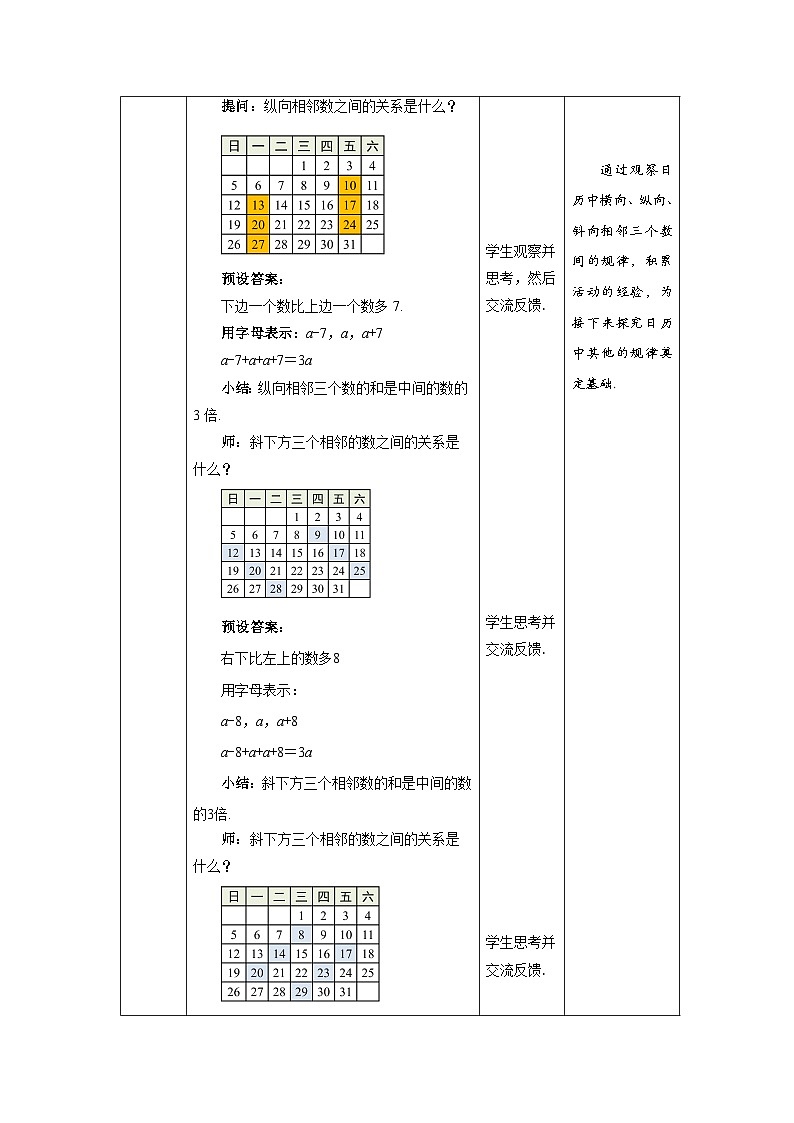
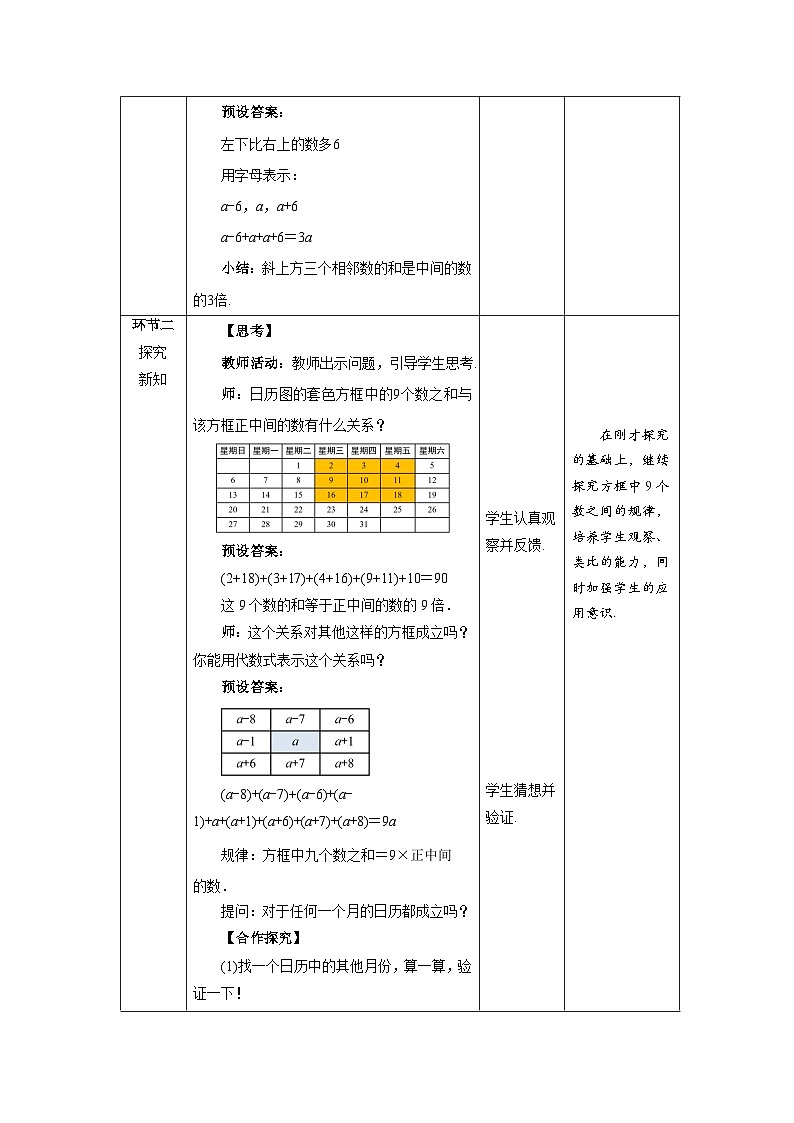
第三章 整式及其加减5 探索与表达规律一、教学目标1.经历由特殊到一般和由一般到特殊的过程，体会代数推理的特点和作用；2.能用代数式表示并借助代数式运算验证探索规律的一般性；3.能运用所总结的规律解决问题；4.在解决实际问题中培养应用意识以及独立解决问题的能力. 二、教学重难点重点：能用代数式表示并借助代数式运算验证探索规律的一般性.难点：能运用所总结的规律解决问题.三、教学用具电脑、多媒体、课件、教学用具等四、教学过程设计教学环节教师活动学生活动设计意图环节一创设情境【情境导入】教师活动：教师出示问题，引发学生思考.师：观察下图日历，请你回答以下问题：(1)横向相邻数之间的关系是什么？预设答案：后一个数比前一个数多1.用字母表示：a-1，a，a+1a-1+a+a+1＝3a小结：横向相邻三个数的和是中间的数的3倍. 提问：纵向相邻数之间的关系是什么？预设答案：下边一个数比上边一个数多7.用字母表示：a-7，a，a+7a-7+a+a+7＝3a小结：纵向相邻三个数的和是中间的数的3倍.师：斜下方三个相邻的数之间的关系是什么？预设答案：右下比左上的数多8用字母表示：a-8，a，a+8a-8+a+a+8＝3a小结：斜下方三个相邻数的和是中间的数的3倍.师：斜下方三个相邻的数之间的关系是什么？预设答案：左下比右上的数多6用字母表示：a-6，a，a+6a-6+a+a+6＝3a小结：斜上方三个相邻数的和是中间的数的3倍.           学生观察并思考，然后交流反馈.          学生观察并思考，然后交流反馈.            学生思考并交流反馈.           学生思考并交流反馈.                  通过观察日历中横向、纵向、斜向相邻三个数间的规律，积累活动的经验，为接下来探究日历中其他的规律奠定基础.      环节二探究新知【思考】教师活动：教师出示问题，引导学生思考.师：日历图的套色方框中的9个数之和与该方框正中间的数有什么关系？预设答案：(2+18)+(3+17)+(4+16)+(9+11)+10＝90 这9个数的和等于正中间的数的9倍．师：这个关系对其他这样的方框成立吗？你能用代数式表示这个关系吗？预设答案：(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)＝9a规律：方框中九个数之和＝9×正中间的数．提问：对于任何一个月的日历都成立吗？【合作探究】(1)找一个日历中的其他月份，算一算，验证一下！ (2)你还能发现方框中这9个数之间的其他关系吗？用代数式表示一下！【归纳】在日历中，方框中的9个数之和是最中间数的9倍.如果用a表示正中间的数，这9个数的和等于9a．任意一行或列的三个数值和等于最中间数的3倍如果设最中间的数为a，则任意一行或列的三个数的和为3a【想一想】如果将方框改为十字形框，你能发现哪些规律？预设答案：7+13+14+15+21＝70＝14×5十字形中5个数的和等于正中间的数的5倍．提问：如果将方框改为H形框，你能发现哪些规律？预设答案：10+12+17+18+19+24+26＝126＝18×7H形框中7个数的和等于正中间的数的7倍．师：你还能设计其它形状的包含数字规律的数框吗？预设答案：8+10+16+22+24＝80＝10×5X形框中5个数的和等于正中间的数的5倍．【思考】小明：你在心里想好一个两位数，将十位数字乘以2，然后加上3，再把所得新数乘以5，最后把得到的新数加上个位数字，把你的结果告诉我，我就知道你心里想的两位数.你知道小明是怎么算出来的吗？预设答案：如果用a，b分别表示一个两位数的十位数字和个位数字，那么这个两位数可以表示为10a+b.5(2a+3)+b=10a+b+15      结论：得到的结果为原两位数与15的和.【做一做】设计类似的数字游戏，并解释其中的道理小组合作探究：小组成员相互协作，设计一个数字游戏，然后相互交流一下.预设答案：你在心里想好一个数，按照下列步骤进行运算：这个数乘4→加8 →所得新数乘5 →再加7 →得到的数乘5.把你的结果告诉我，我就知道你心里想的数了.5×[5(4a+8)+7]＝100a+235      结论：只要把计算结果减235，再除以100，就是心里所想的数.        学生认真观察并反馈.         学生猜想并验证.       学生小组活动并交流反馈.      学生归纳总结.     学生观察并思考，然后交流反馈.             学生思考并回答.            学生用发现的规律算一算，并交流反馈.                 学生尝试验证并交流反馈.       学生小组合作设计游戏，然后交流反馈.           在刚才探究的基础上，继续探究方框中9个数之间的规律，培养学生观察、类比的能力，同时加强学生的应用意识.                通过小组活动的形式进行探究，培养学生团结写作的学习能力，激发学生不断的思考，提升学习兴趣.      在同一情境下探究不同的规律，让学生体会规律的多样性，并让学生用字母表示，并借助运算验证规律，并将具体规律推广到一般.             让学生自己找寻规律并探究，巩固所学知识的同时，激发学生的探索欲，提升学习兴趣.       给定规律或现象，让学生通过运算解释规律或现象，并且采用游戏的形式进行，激发学生探究的兴趣.            通过小组合作的形式设计游戏，不仅增强了学生间的合作意识，同时也让学生体会到合作带来的乐趣，提升学习兴趣.     环节三应用新知【典型例题】教师活动：教师给出例题，学生先独立思考，解答. 然后再小组交流探讨，如遇到有困难的学生适当点拨，最终教师展示答题过程. 例1 下面是用棋子摆成的“小房子”.第10个这样的“小房子”需要多少枚棋子？摆第n个这样的“小房子”呢？分析：后边的“小房子”总比前边一个多用6枚棋子.解：5+6(n-1)＝6n-1当n＝10，6×10-1＝59答：第10个这样的“小房子”需要59枚棋子.    摆第n个这样的“小房子”，需要6n-1枚棋子.例2 有三堆棋子，数目相等，每堆至少有4枚. 从左堆中取出3枚放入中堆，从右堆中取出4枚放入中堆，再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆，这时中堆的棋子数是多少？请做一做，并解释其中的道理.解：设三堆棋子数均为a，中堆的棋子数为a+3+4-(a-3)＝10(枚)答：中堆的棋子数是10枚.        学生认真思考并作答.                学生思考并反馈.          通过例题的探究，让学生进一步体会规律的多样性，学会用找到的规律解决实际问题，加强学生的应用意识.      环节四巩固新知【随堂练习】教师活动：教师给出练习，随时观察学生完成情况并相应指导，最后给出答案，根据学生完成情况适当分析讲解.1.用正方形套住日历中的任意 9 个数，若中间的数是 14，则这 9 个数的和是______．分析：在日历中，方框中的9个数之和是最中间数的9倍．如果用a表示正中间的数，这9个数的和等于9a．答案：126.2. (1)按图①方式摆放餐桌和椅子，照这样的方式继续排列餐桌，摆4张桌子可坐多少人？摆5张桌子呢？摆n张桌子呢？ (2)按图②方式摆放餐桌和椅子，照这样的方式继续排列餐桌，摆4张桌子可坐多少人？摆5张桌子呢？摆n张桌子呢？  答案：(1)摆4张桌子可坐12人，摆5张桌子可坐14人.摆n张桌子可坐(2n+4)人.(2)摆4张桌子可坐18人，摆5张桌子可坐22人.摆n张桌子可坐(4n+2)人.3.将连续的奇数1，3，5，7，9，….排成如图所示的数表. (1)十字形框中的五个数之和与中间数15有什么关系？(2)设中间数为a，如何用代数式表示十字形框中五个数之和？(3)若将十字形框上下左右移动，可框住另外五个数，这五个数还有上述的规律吗？(4)十字形框中的五数之和能等于2012吗？能等于2015吗？答案：(1)十字形框中的五个数之和是中间数15的5倍.(2)十字形框中的五个数分别为a，a-10，a-2，a+2，a+10，它们的和是5a.(3)有.(4)十字形框中的五数之和不能等于2012，能等于2015.             先自主完成练习，再集体交流评价       通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养学生独立完成练习的习惯. 环节五课堂小结思维导图的形式呈现本节课的主要内容：   回顾本节课所讲的内容通过小结总结回顾本节课学习内容，帮助学生归纳、巩固所学知识.环节六布置作业 教科书第100页习题3.9第2、3题  课后独立完成练习通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.