2023年江苏省无锡市梁溪区中考二模数学试题（含答案）

这是一份2023年江苏省无锡市梁溪区中考二模数学试题（含答案），共10页。试卷主要包含了05，000021千克，数据0等内容，欢迎下载使用。
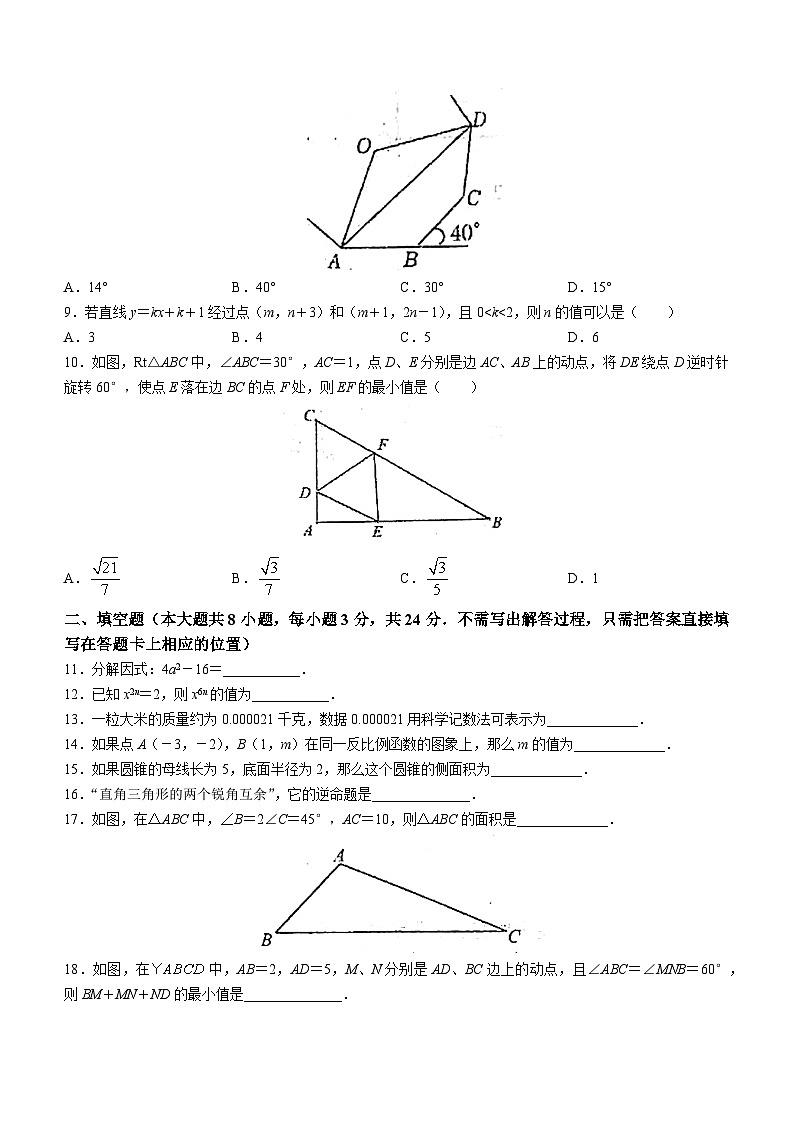
2023年九年级第二次适应性练习数学试题2023.05本试卷分试题卷和答题卷两部分，所有答案一律写在答题卷上。考试时间为120分钟，试卷满分为150分。一、选择题（本大题共10小题，每小题3分，共30分．在每小题所给出的四个选项中，只有一项是正确的，请用2B铅笔把答题卡上相应的选项标号涂黑）1．下列各数中，绝对值最小的数是（    ）A．0 B．－1 C． D．2．下列运算正确的是（    ）A． B． C． D．3．函数中自变量x的取值范围是（    ）A．x≤2 B．x≥2 C．x<2 D．x>24．为了调查我市某校学生的视力情况，在全校的2000名学生中随机抽取了300名学生，下列说法正确的是（    ）A．此次调查属于全面调查  B．样本容量是300C．2000名学生是总体  D．被抽取的每一名学生称为个体5．下列图形是中心对称图形但不是轴对称图形的是（    ）A．平行四边形 B．等边三角形 C．圆 D．线段6．如图，一个圆柱体在正方体上表面沿虚线从左向右平移，则该组合体在该平移过程中不变的视图是（    ）A．主视图和俯视图 B．主视图 C．俯视图 D．左视图7．下列命题中：①菱形的对角线相等；②矩形的对角线互相垂直；③平行四边形的对角线互相平分；④正方形的对角线相等且互相垂直平分．真命题的个数为（    ）A．0 B．1 C．2 D．38．如图，A、B、C、D是一个外角为40°的正多边形的顶点．若O为正多边形的中心，则∠OAD的度数为（    ）A．14° B．40° C．30° D．15°9．若直线y＝kx＋k＋1经过点（m，n＋3）和（m＋1，2n－1），且0<k<2，则n的值可以是（    ）A．3 B．4 C．5 D．610．如图，Rt△ABC中，∠ABC＝30°，AC＝1，点D、E分别是边AC、AB上的动点，将DE绕点D逆时针旋转60°，使点E落在边BC的点F处，则EF的最小值是（    ）A． B． C． D．1二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）11．分解因式：4a2－16＝___________．12．已知x2n＝2，则x6n的值为___________．13．一粒大米的质量约为0.000021千克，数据0.000021用科学记数法可表示为_____________．14．如果点A（－3，－2），B（1，m）在同一反比例函数的图象上，那么m的值为_____________．15．如果圆锥的母线长为5，底面半径为2，那么这个圆锥的侧面积为_____________．16．“直角三角形的两个锐角互余”，它的逆命题是______________．17．如图，在△ABC中，∠B＝2∠C＝45°，AC＝10，则△ABC的面积是_____________．18．如图，在中，AB＝2，AD＝5，M、N分别是AD、BC边上的动点，且∠ABC＝∠MNB＝60°，则BM＋MN＋ND的最小值是______________．三、解答题（本大题共10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）19．（本题满分8分）计算：（1）；    （2）（x＋y）（x－y）－x（x－2y）．20．（本题满分8分）（1）解方程：；       （2）解不等式组：21．（本题满分10分）如图，点E在△ABC边AC上，AE＝BC，，∠CED＝∠BAD．（1）求证：△ABC≌△DEA；（2）若∠ACB＝30°，求∠BCD的度数．22．（本题满分10分）为了让同学们进一步了解中国科技的快速发展，某中学九（1）班团支部组织了一次手抄报比赛，该班每位同学从A．“中国天眼”，B．“5G时代”，C．“夸父一号”，D．“巅峰使命”四主题中任选一个自己喜欢的主题．统计同学们所选主题的频数，绘制了不完整的统计图如下，请根据统计图中的信息解答下列问题：（1）九（1）班共有_________名学生；（2）请以九（1）班的统计数据估计全校2000名学生大约有多少人选择D主题？（3）甲和乙从A、B、C、D四个主题中任选一个主题，请用列表法或画树状图法求出他们选择相同主题的概率．23．（本题满分10分）如图，AB是⊙O的直径，点C在⊙O上，∠CAB的平分线与BC相交于点D，与⊙O过点B的切线相交于点E．（1）判断△BDE的形状，并证明你的结论；（2）若AB＝4，BD＝2，求AD的长．24．（本题满分10分）我市为了打造湿地公园，今年计划改造一片绿化地种植A、B两种景观树．种植3棵A种、4棵B种景观树需要1800元，种植4棵A种、3棵B种景观树需要1700元．（1）种植每棵A种景观树和每棵B种景观树各需要多少元？（2）今年计划种植A、B两种景观树共400棵，且A种景观树的数量不超过B种景观树数量的3倍，那么种植这两种景观树的总费用最低为多少元？（3）相关资料表明：A、B两种景观树的成活率分别为70%和90%．今年计划投入10万元种植A、B两种景观树共400棵，要求这两种树的总成活率不低于85%，投入的钱是否够用？请说明理由．25．（本题满分10分）如图，函数的图象分别交x轴、y轴于M、N两点，过线段MN上两点A、B分别作x轴的垂线，垂足为A1、B1，记△OAA1的面积为S1，△OBB1的面积为S2．（1）若点A的横坐标为2，求S1的值；（2）若OA1＋OB1>4，求证：S1>S2．26．（本题满分10分）定义：如图1，点C把线段AB分成两部分，如果，那么点C为线段AB的“白银分割点”．应用：（1）如图2，矩形ABCD中，AB＝1，，E为CD上一点，将矩形ABCD沿BE折叠，使得点C落在AD边上的点F处，延长BF交CD的延长线于点G，说明点E为线段GC的“白银分割点”．（2）已知线段AB（如图3），作线段AB的一个“白银分割点”，（要求：尺规作图，保留作图痕迹，不写作法）27．（本题满分10分）如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋4与x轴交于A（－6，0）、B（2，0）两点，与y轴交于点C，点P为直线AC上方抛物线上一动点，连接OP交AC于点Q．（1）求抛物线的函数表达式；（2）当的值最大时，求点P的坐标和的最大值；（3）若点M是抛物线对称轴上一动点，点N是平面内任意一点，当以A、C、M、N为顶点的四边形为菱形时，直接写出点N的坐标．28．（本题满分10分）已知：在矩形ABCD中，AB＝3，AD＝4，点P是DC边上的一个动点，将矩形ABCD折叠，使点B与点P重合，点A落在点G处，折痕为EF．（1）如图1，当点P与点D、C均不重合时，取EF的中点O，连接PO并延长与GF的延长线交于点M，连接PF、ME、MB．①求证：四边形MEPF是平行四边形；②当时，求四边形MEPF的面积．（2）如图2，设PC＝t，用含t的式子表示四边形ECDF的面积S，并求出S的最大值及此时t的值．2023年九年级第二次适应性练习数学答案2023.05一、选择题（本大题共10小题，每小题3分，共30分．）1．A  2．B  3．A  4．B  5．A  6．D  7．C  8．C  9．C  10．A二、填空题（本大题共8小题，每小题3分，共24分．）11．4（a＋2）（a－2）    12．8    13．2.1×10－5    14．6    15．16．两角互余的三角形是直角三角形    17．25   18．三、解答题（本大题共10小题，共96分．）19．（1）解：原式       （2）解：原式                                        20．（1）解：2x＝－1＋x－3            （2）解：由①得：x＞－1             x＝－4                         由②得：x≤4经检验：x＝－4是原方程的解                 ∴－1<x≤4．21．⑴证明：∵，∴∠DAC＝∠ACB，∵∠CED＝∠BAD，∠CED＝∠ADE＋∠DAC，∠BAD＝∠DAC＋∠BAC，∴∠ADE＝∠BAC，在△ABC和△DEA，∴△ABC≌△DEA（AAS）．⑵∵△ABC≌△DEA，∴AC＝AD∵∠DAC＝∠ACB，∠ACB＝30°∴∠DAC＝30°∴∠ACD＝75°∴∠BCD＝∠BCA＋∠ACD＝105°．22．解：（1）50；    （2）（人）．∴估计全校2000名学生大约有600人选择D主题．（3）画树状图如下：由上图可知共有16种等可能的结果，其中他们选择相同主题的结果有4种是：（A，A）、（B，B），（C，C），（D，D）∴P（甲乙选择相同主题）．23．证明：∵AE平分∠BAC，∴∠BAE＝∠CAE，∵AB为直径，∴∠C＝90°，∴∠CAD＋∠ADC＝90°，∵BE切⊙O于B，∴AB⊥BE，∴∠BAE＋∠E＝90°，∴∠ADC＝∠E，而∠ADC＝∠BDE，∴∠BDE＝∠E，∴BE＝BD，∴△BDE是等腰三角形．（2）解：∵∠BAE＝∠CAD，∴Rt△ACD∽Rt△ABE，∴CD∶AC＝BE∶AB＝2∶4，设CD＝x，AC＝2x，则，在Rt△ABC中，BC＝BD＋CD＝x＋2，∵（2x）2＋（2＋x）2＝42，解得，（舍去），∴．24．解：（1）设种植每棵A种景观树需要a元，每棵B种景观树需要b元，根据题意得：，解得：．答：种植每棵A种景观树需要200元，每棵B种景观树需要300元；（2）设种植A种景观树x棵，则种植B种景观树（400－x）棵，根据题意得：y＝200x＋300（400－x）＝－100x＋120000，∵A种景观树的数量不超过B种景观树数量的3倍，∴x≤3（400－x），∴x≤300，∵－100<0，∴y随x的增大而减小，∴当x＝300时，y最小＝－30000＋120000＝90000（元），∴这两种景观树的总费用最低为90000元；（3）投入的钱不够用．理由：∵70%x＋（400－x）×90%≥400×85%，∴x≤100，∵y＝100x＋120000≤100000，∴x≥200，∴投入的钱不够用．25．（1）当x＝2时，，∴（2，1）∴（2）设A、B两点的横坐标分别为x1、x2，且0<x1<x2<4于是、、，，∴∴26．（1）∵四边形ABCD是矩形，∴∠A＝90°＝∠C，∵矩形ABCD沿BE折叠，使得点C落在AD边上的点F处，∴，∠BFE＝∠C＝90°＝∠GFE，EF＝CE，∵AB＝1，∴∴AB＝AF，∴△ABF是等腰直角三角形，∠AFB＝45°＝∠GFD，∵∠ADC＝90°＝∠ADG，∴∠G＝45°，∴△GFE的等腰直角三角形，∴，∴，∴E是线段GC的“白银分割点”（2）作法：过B作BH⊥AB，在BH上取BE＝AB，连接AE，作∠AEB的角平分线交AB于K，点K即为线段AB的“白银分割点”．27．（1）不妨设抛物线为y＝a（x＋6）（x－2），由－12a＝4，得故抛物线的函数表达式是（2）过点P作y轴的平行线，交线段BC于点K，可设，，∵∴当t＝－3，即P（－3，5）时，（3），，N（4，10）、N（4，－2）28．（1）①∵纸片折叠，仍有，∴∠FMO＝∠EPO，∠MFO＝∠PEO，又∵OF＝OE，∴△MOF≌△POE，∴OM＝OP，∴四边形MEPF是平行四边形．②连结PB，交EF于点N，∵沿EF折叠使点B与点P重合，∴EF⊥BP，BN＝PN，设BE＝PE＝a又∵OM＝OP，∴ON是△PBM的中位线，∴∠MBP＝∠FNP＝90°＝∠ABC，∴∠PBC＝∠ABM在矩形ABCD中，∠C＝90°，，BC＝AD＝4，∴PC＝2∴在Rt△PBC中，a2＝22＋（4－a）2，解得，∴（2）连结BP、BF、PF，设四边形ECDF中，CE＝a，DF＝b在Rt△PEC中，，∴由BF＝PF，得，∴∴故当时，．