

2023年广东省东莞市宏远外国语学校中考数学一模试卷(含解析)
展开
这是一份2023年广东省东莞市宏远外国语学校中考数学一模试卷(含解析),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年广东省东莞市宏远外国语学校中考数学一模试卷
一、选择题(每小题3分,共30分)
1.(3分)下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(3分)下列计算正确的是( )
A.x2+x2=x4 B.(x﹣y)2=x2﹣y2
C.(x2y)3=x6y D.(﹣x)2•x3=x5
3.(3分)2022年5月17日,工业和信息化部负责人在“2022世界电信和信息社会日”大会上宣布,我国目前已建成5G基站近160万个,成为全球首个基于独立组网模式规模建设5G网络的国家.将数据160万用科学记数法表示为( )
A.1.6×102 B.1.6×105 C.1.6×106 D.1.6×107
4.(3分)某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如右表:
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
A.3,3 B.3,7 C.2,7 D.7,3
5.(3分)关于x的一元二次方程x2+2mx+m2﹣m=0的两实数根x1,x2,满足x1x2=2,则的值是( )
A.8 B.16 C.32 D.16或40
6.(3分)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
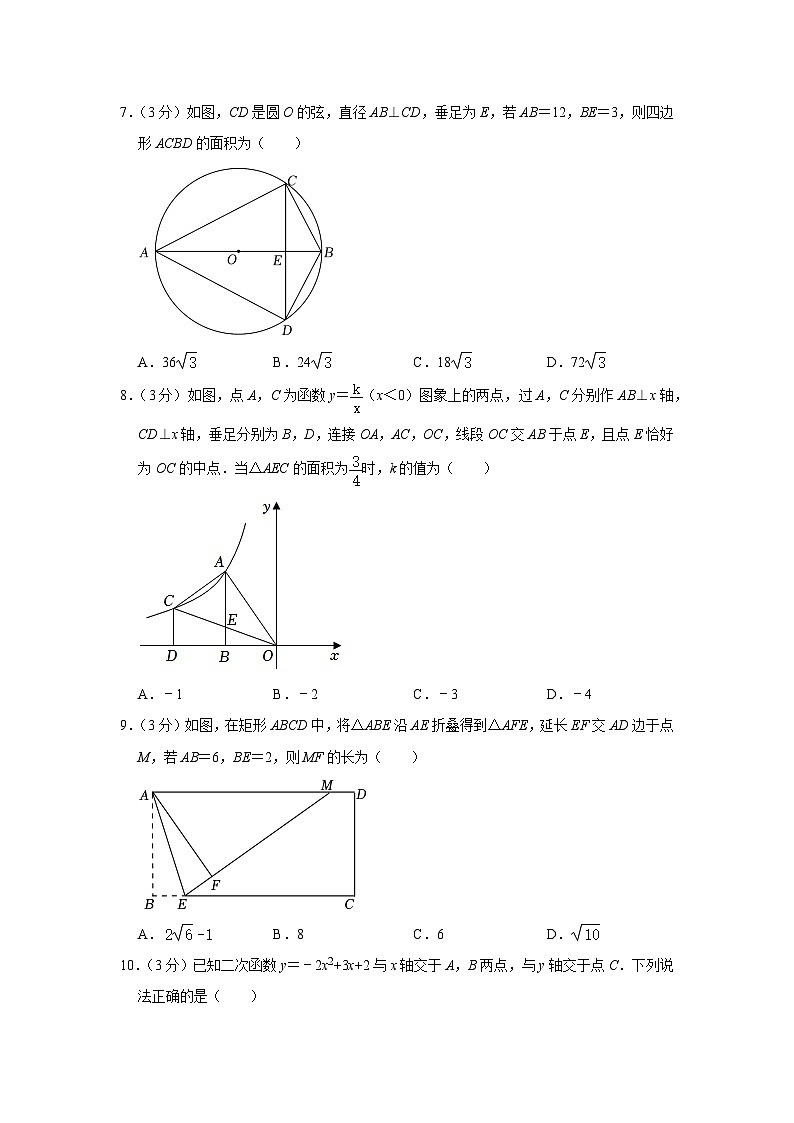
7.(3分)如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
8.(3分)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
9.(3分)如图,在矩形ABCD中,将△ABE沿AE折叠得到△AFE,延长EF交AD边于点M,若AB=6,BE=2,则MF的长为( )
A. B.8 C.6 D.
10.(3分)已知二次函数y=﹣2x2+3x+2与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )
①线段AC的长度为;②抛物线的对称轴为直线x=;③P是此抛物线的对称轴上的一个动点,当P点坐标为(,)时,|PA﹣PC|的值最大;④若M是x轴上的一个动点,N是此抛物线上的一个动点,如果以A,C,M,N为顶点的四边形是平行四边形,满足条件的M点有4个.
A.①② B.①②③ C.①②④ D.③④
二、填空题(每小题4分,共28分)
11.(4分)不透明袋子中装有3个红球,5个黑球,4个白球,这些球除颜色外无其他差别,从袋子中随机摸出一个球,则摸出红球的概率是 .
12.(4分)因式分解:x3﹣6x2+9x= .
13.(4分)关于x的分式方程+2=0的解为正数,则m的取值范围是 .
14.(4分)若关于x的不等式组有且仅有3个整数解,a的取值范围是 .
15.(4分)一个多边形的内角和与外角和的总和为1980°,则这个多边形的边数为 .
16.(4分)如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB是一元二次方程x2﹣10x+24=0的两根,则cos∠BPD是 .
17.(4分)如图,直线与y轴交于点A,与双曲线在第三象限交于B、C两点,且AB•AC=16;下列等边三角形△E1D1E1,△E1D2E2,△E2D3E3,……的边OE1,E1E2,E2E3,……在x轴上,顶点D1,D2,D3,……在该双曲线第一象限的分支上,则k= ,前25个等边三角形的周长之和为 .
三、解答题(一)(每小题6分,共18分)
18.(6分)计算:.
19.(6分)先化简,再求值:(1﹣)÷,其中x=3+.
20.(6分)成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D处测得塔A处的仰角为45°,塔底部B处的俯角为22°.已知建筑物的高CD约为61米,请计算观景台的高AB的值.
(结果精确到1米;参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
四、解答题(二)(每小题8分,共24分)
21.(8分)为了弘扬爱国主义精神,某校组织了“共和国成就”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制了如图统计图.
(1)本次抽样调查的样本容量是 ,请补全条形统计图;
(2)已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;
(3)该校共有2000名学生,请你估计该校竞赛成绩“优秀”的学生人数.
22.(8分)某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨.
(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
23.(8分)如图,在四边形ABCD中,AB∥CD,BD交AC于G,E是BD的中点,连接AE并延长,交CD于点F,F恰好是CD的中点.
(1)求的值;
(2)若CE=EB,求证:四边形ABCF是矩形.
五、解答题(三)(每小题10分,共20分)
24.(10分)如图,⊙O是△ABC的外接圆,AB为直径,点P为⊙O外一点,且PA=PC=AB,连接PO交AC于点D,延长PO交⊙O于点F.
(1)证明:=;
(2)若tan∠ABC=2,证明:PA是⊙O的切线;
(3)在(2)条件下,连接PB交⊙O于点E,连接DE,若BC=2,求DE的长.
25.(10分)在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记△BDE的面积为S1,△ABE的面积为S2,求的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点.试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
2023年广东省东莞市宏远外国语学校中考数学一模试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列图标中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、不是轴对称图形,是中心对称图形,故本选项错误;
C、是轴对称图形,不是中心对称图形,故本选项错误;
D、既是轴对称图形,又是中心对称图形,故本选项正确.
故选:D.
2.(3分)下列计算正确的是( )
A.x2+x2=x4 B.(x﹣y)2=x2﹣y2
C.(x2y)3=x6y D.(﹣x)2•x3=x5
【分析】根据合并同类项法则、完全平方公式、积的乘方法则、同底数幂的乘法法则计算,判断即可.
【解答】解:x2+x2=2x2,A错误;
(x﹣y)2=x2﹣2xy+y2,B错误;
(x2y)3=x6y3,C错误;
(﹣x)2•x3=x2•x3=x5,D正确;
故选:D.
3.(3分)2022年5月17日,工业和信息化部负责人在“2022世界电信和信息社会日”大会上宣布,我国目前已建成5G基站近160万个,成为全球首个基于独立组网模式规模建设5G网络的国家.将数据160万用科学记数法表示为( )
A.1.6×102 B.1.6×105 C.1.6×106 D.1.6×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:160万=1600000=1.6×106,
故选:C.
4.(3分)某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如右表:
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
A.3,3 B.3,7 C.2,7 D.7,3
【分析】根据众数、中位数的定义分别进行解答即可.
【解答】解:因为共有20个数据,
所以中位数为第10、11个数据的平均数,即中位数为=3,
由表格知数据3出现了7次,次数最多,所以众数为3.
故选:A.
5.(3分)关于x的一元二次方程x2+2mx+m2﹣m=0的两实数根x1,x2,满足x1x2=2,则的值是( )
A.8 B.16 C.32 D.16或40
【分析】先根据根的判别式求得m的取值范围,然后根据一元二次方程根与系数的关系得到x1+x2=﹣2m,x1•x2=m2﹣m=2,进而求得m=2或m=﹣1,从而求得x1+x2=﹣4,把原式变形,代入计算即可.
【解答】解:由题意得Δ=(2m)2﹣4(m2﹣m)≥0,
∴m≥0,
∵关于x的一元二次方程x2+2mx+m2﹣m=0的两实数根x1,x2,满足x1x2=2,
则x1+x2=﹣2m,x1•x2=m2﹣m=2,
∴m2﹣m﹣2=0,解得m=2或m=﹣1(舍去),
∴x1+x2=﹣4,
(+2)(+2)
=(x1x2)2+2(x1+x2)2﹣4x1x2+4,
原式=22+2×(﹣4)2﹣4×2+4=32.
故选:C.
6.(3分)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
【分析】先根据反比例函数y=判断此函数图象所在的象限,再根据x1<0<x2判断出A(x1,y1)、B(x2,y2)所在的象限即可得到答案.
【解答】解:∵反比例函数y=中的6>0,
∴该双曲线位于第一、三象限,且在每一象限内y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,
∴点A位于第三象限,点B位于第一象限,
∴y1<y2.
故选:C.
7.(3分)如图,CD是圆O的弦,直径AB⊥CD,垂足为E,若AB=12,BE=3,则四边形ACBD的面积为( )
A.36 B.24 C.18 D.72
【分析】根据AB=12,BE=3,求出OE=3,OC=6,并利用勾股定理求出EC,根据垂径定理求出CD,即可求出四边形的面积.
【解答】解:如图,连接OC,
∵AB=12,BE=3,
∴OB=OC=6,OE=3,
∵AB⊥CD,
在Rt△COE中,EC=,
∴CD=2CE=6,
∴四边形ACBD的面积=.
故选:A.
8.(3分)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【分析】根据三角形的中线的性质求出△AEO的面积,根据相似三角形的性质求出S△OCD=1,根据反比例函数系数k的几何意义解答即可.
【解答】解:∵点E为OC的中点,
∴△AEO的面积=△AEC的面积=,
∵点A,C为函数y=(x<0)图象上的两点,
∴S△ABO=S△CDO,
∴S四边形CDBE=S△AEO=,
∵EB∥CD,
∴△OEB∽△OCD,
∴=()2,
∴S△OCD=1,
则xy=﹣1,
∴k=xy=﹣2.
故选:B.
9.(3分)如图,在矩形ABCD中,将△ABE沿AE折叠得到△AFE,延长EF交AD边于点M,若AB=6,BE=2,则MF的长为( )
A. B.8 C.6 D.
【分析】作MN⊥BC于点N,由折叠得EF=BE=2,AF=AB=6,∠AFE=∠B=90°.再用”AAS“证明△AFM≌△MNE得ME=AM,在直角三角形AMF中使用勾股定理建立方程求解即可.
【解答】解:如图,作MN⊥BC于点N,
由折叠可得:△ABE≌△AFE.
∴EF=BE=2,AF=AB=6,∠AFE=∠B=90°,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AME=∠CEM,
又MN⊥BC,
∴MN=AB=AF=6,∠MNE=∠AFM=90°,
在△AFM和△MNE中,
,
∴△AFM≌△MNE(AAS).
∴AM=ME,
设MF=x,则AM=ME=x+2,
在直角三角形AMF中,由勾股定理有:AM2=AF2+MF2,
即(x+2)2=36+x2,解得:x=8.
故MF=8.
故选:B.
10.(3分)已知二次函数y=﹣2x2+3x+2与x轴交于A,B两点,与y轴交于点C.下列说法正确的是( )
①线段AC的长度为;②抛物线的对称轴为直线x=;③P是此抛物线的对称轴上的一个动点,当P点坐标为(,)时,|PA﹣PC|的值最大;④若M是x轴上的一个动点,N是此抛物线上的一个动点,如果以A,C,M,N为顶点的四边形是平行四边形,满足条件的M点有4个.
A.①② B.①②③ C.①②④ D.③④
【分析】求得抛物线与坐标轴的交点,然后根据勾股定理求得AC,即可判断①;根据对称轴方程求得对称轴,即可判断②;求得直线AC的解析式,求得直线AC与对称轴的交点即可判断③;分两种情况讨论根据平行四边形的性质求得M的坐标,即可判断④.
【解答】解:①二次函数y=﹣2x2+3x+2与x轴交于A,B两点,与y轴交于点C,
∴x=0时,y=2,当y=0时,则﹣2x2+3x+2=0,解得x1=﹣,x2=2,
∴A(﹣,0),B(2,0),C(0,2),
∴OA=,OC=2,
∴AC==,故说法①正确;
②∵y=﹣2x2+3x+2,
∴抛物线的对称轴为直线x=﹣=,故说法②正确;
③∴A(﹣,0),C(0,2),
∴直线AC为y=4x+2,
把x=代入得,y=4×+2=5,
∴当P点坐标为(,5)时,|PA﹣PC|的值最大,故说法③错误;
④当AM=NC,则M(1,0)或(﹣2,0),
当AC=MN,则M(,0)或(,0),
综上所述:点M的坐标分别是(1,0)或(﹣2,0)或(,0)或(,0)共4个,故说法④正确;
故选:C.
二、填空题(每小题4分,共28分)
11.(4分)不透明袋子中装有3个红球,5个黑球,4个白球,这些球除颜色外无其他差别,从袋子中随机摸出一个球,则摸出红球的概率是 .
【分析】用红色球的个数除以球的总个数即可.
【解答】解:∵袋子中共有3+5+4=12个除颜色外无其他差别的球,其中红球的个数为3,
∴从袋子中随机摸出一个球,摸出红球的概率是=,
故答案为:.
12.(4分)因式分解:x3﹣6x2+9x= x(x﹣3)2 .
【分析】原式提取x,再利用完全平方公式分解即可.
【解答】解:原式=x(x2﹣6x+9)=x(x﹣3)2,
故答案为:x(x﹣3)2
13.(4分)关于x的分式方程+2=0的解为正数,则m的取值范围是 m<2且m≠0 .
【分析】首先解方程求得方程的解,根据方程的解是正数,即可得到一个关于m的不等式,从而求得m的范围.
【解答】解:去分母得:m+4x﹣2=0,
解得:x=,
∵关于x的分式方程+2=0的解是正数,
∴>0,
∴m<2,
∵2x﹣1≠0,
∴2×﹣1≠0,
∴m≠0,
∴m的取值范围是m<2且m≠0.
故答案为:m<2且m≠0.
14.(4分)若关于x的不等式组有且仅有3个整数解,a的取值范围是 ﹣7≤a<﹣3 .
【分析】先求出每个不等式的解集,再求出不等式组的解集,即可得出答案.
【解答】解:,
解不等式①得:x,
解不等式②得:x>,
∵关于x的不等式组有且仅有3个整数解,
∴﹣2≤<﹣1,
∴﹣7≤a<﹣3,
故答案为:﹣7≤a<﹣3.
15.(4分)一个多边形的内角和与外角和的总和为1980°,则这个多边形的边数为 11 .
【分析】依题意,多边形的内角与外角和为1980°,多边形的外角和为360°,根据内角和公式求出多边形的边数.
【解答】解:设多边形的边数为n,根据题意列方程得,
(n﹣2)•180°+360°=1980°,
n﹣2=9,
n=11.
故答案为:11.
16.(4分)如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB是一元二次方程x2﹣10x+24=0的两根,则cos∠BPD是 .
【分析】连接BD,解方程求出CD,AB的长,证△DPC∽△BPA,根据相似三角形的性质得到DP与BP的关系,即可求解.
【解答】解:x2﹣10x+24=0,
解得x1=4,x2=6,
即CD=4,AB=6.
如图,连接BD,
∵∠CDP=∠ABP,∠C=∠A,
∴△DPC∽△BPA,
∴.
∵AB为半圆O的直径,
∴∠ADB=90°.
∴.
故答案为:.
17.(4分)如图,直线与y轴交于点A,与双曲线在第三象限交于B、C两点,且AB•AC=16;下列等边三角形△E1D1E1,△E1D2E2,△E2D3E3,……的边OE1,E1E2,E2E3,……在x轴上,顶点D1,D2,D3,……在该双曲线第一象限的分支上,则k= 4 ,前25个等边三角形的周长之和为 60 .
【分析】设直线y=﹣x+b与x轴交于点D,作BE⊥y轴于E,CF⊥y轴于F.首先证明∠ADO=60°,可得AB=2BE,AC=2CF,由直线y=﹣x+b与双曲线y=在第三象限交于点B、C两点,可得﹣x+b=,整理得,﹣x2+bx﹣k=0,由韦达定理得:x1x2=k,即EB•FC=k,由此构建方程求出k即可,第二个问题分别求出第一个,第二个,第三个,第四个三角形的周长,探究规律后解决问题.
【解答】解:设直线y=﹣x+b与x轴交于点D,作BE⊥y轴于E,CF⊥y轴于F,
∵y=﹣x+b,
∴当y=0时,x=b,
即点D的坐标为(b,0),
当x=0时,y=b,
即A点坐标为(0,b),
∴OA=﹣b,OD=﹣b.
在Rt△AOD中,tan∠ADO==,
∴∠ADO=60°.
∵直线y=﹣x+b与双曲线y=在第三象限交于B、C两点,
∴﹣x+b=,
整理得:﹣x2+bx﹣k=0,
由根与系数的关系得:x1x2=k,
即EB•FC=k,
∵=cos60°=,
∴AB=2EB,
同理可得:AC=2FC,
∴AB•AC=(2EB)(2FC)=4EB•FC=k=16,
解得:k=4.
由题意可以假设D1(m,m),
∴m2•=4,
∴m=2,
∴OE1=4,
即第一个三角形的周长为12,
设D2(4+n,n),
∵(4+n)•n=4,
解得:n=2﹣2,
∴E1E2=4﹣4,
即第二个三角形的周长为12﹣12,
设D3(4+a,a),
由题意(4+a)•a=4,
解得a=2﹣2,
即第三个三角形的周长为12﹣12,
…,
∴第四个三角形的周长为12﹣12,
∴前25个等边三角形的周长之和为:12+12﹣12+12﹣12+12﹣12+…+12﹣12=12=60,
故答案为:4,60.
三、解答题(一)(每小题6分,共18分)
18.(6分)计算:.
【分析】直接利用负整数指数幂的性质和绝对值的性质、特殊角的三角函数值分别化简,然后先算乘法,再算加减得出答案.
【解答】解:原式=
=
=3.
19.(6分)先化简,再求值:(1﹣)÷,其中x=3+.
【分析】直接将括号里面通分运算,再利用分式的混合运算法则计算得出答案.
【解答】解:原式=•
=x﹣3,
当x=3+时,
原式=.
20.(6分)成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D处测得塔A处的仰角为45°,塔底部B处的俯角为22°.已知建筑物的高CD约为61米,请计算观景台的高AB的值.
(结果精确到1米;参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
【分析】过点D作DE⊥AB于点E,根据题意可得四边形DCBE是矩形,DE=BC,BE=DC=61,再根据锐角三角函数可得DE的长,进而可得AB的值.
【解答】解:过点D作DE⊥AB于点E,
根据题意可得四边形DCBE是矩形,
∴DE=BC,BE=DC=61(米),
在Rt△ADE中,
∵∠ADE=45°,
∴AE=DE,
∴AE=DE=BC,
在Rt△BDE中,∠BDE=22°,
∴DE=≈=152.5(米),
∴AB=AE+BE=DE+CD=152.5+61=213.5≈214(米).
答:观景台的高AB的值约为214米.
四、解答题(二)(每小题8分,共24分)
21.(8分)为了弘扬爱国主义精神,某校组织了“共和国成就”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制了如图统计图.
(1)本次抽样调查的样本容量是 100 ,请补全条形统计图;
(2)已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;
(3)该校共有2000名学生,请你估计该校竞赛成绩“优秀”的学生人数.
【分析】(1)由已知C等级的人数为25人,所占百分比为25%,25÷25%可得样本容量;利用样本容量可求B,D等级的人数;
(2)依据题意列出表格后求得概率;
(3)利用样本估计总体的思想,用样本的优秀率估计总体的优秀率可得结论.
【解答】解:(1)∵由条形统计图可得C等级的人数为25人,由扇形统计图可得C等级的人数占比为25%,
∴样本容量为25÷25%=100.
∵B等级的人数占比为35%,
∴B等级的人数为:100×35%=35(人).
∴D等级的人数:100﹣35﹣35﹣25=5(人).
补全条形统计图如下:
故答案为:100.
(2)D等级的学生有:100×5%=5(人).
由题意列表如下:
由表格可得,共有20种等可能,其中恰好回访到一男一女的等可能有12种,
∴恰好回访到一男一女的概率为=.
(3)∵样本中A(优秀)的占比为35%,
∴可以估计该校2000名学生中的A(优秀)的占比为35%.
∴估计该校竞赛成绩“优秀”的学生人数为:2000×35%=700(人).
22.(8分)某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨.
(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
【分析】(1)设1辆A货车一次可以运货x吨,1辆B货车一次可以运货y吨,根据3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨列出方程组解答即可;
(2)设A货车运输m吨,则B货车运输(190﹣m)吨,设总费用为w元,列出w的一次函数表达式,化简得w随m的增大而减小;根据A、B两种货车均满载,得,都是整数,分类列举得到符合题意的方案,最后根据费用越少,m越大得到费用最少的方案.
【解答】解:(1)设1辆A货车一次可以运货x吨,1辆B货车一次可以运货y吨,
根据题意得:,
解得:,
答:1辆A货车一次可以运货20吨,1辆B货车一次可以运货15吨;
(2)方法一:设A货车运输m吨,则B货车运输(190﹣m)吨,设总费用为w元,
则:w=500×+400×
=25m+
=25m﹣m+
=﹣m+,
∵﹣<0,
∴w随m的增大而减小.
∵A、B两种货车均满载,
∴,都是大于或等于0的整数,
∴0≤m≤190,
当m=20时,不是整数;
当m=40时,=10;
当m=60时,不是整数;
当m=80时,不是整数;
当m=100时,=6;
当m=120时,不是整数;
当m=140时,不是整数;
当m=160时,=2;
当m=180时,不是整数;
故符合题意的运输方案有三种:
①A货车40÷20=2辆,B货车10辆;
②A货车100÷20=5辆,B货车6辆;
③A货车160÷20=8辆,B货车2辆;
∵w随m的增大而减小,
∴费用越少,m越大,
故方案③费用最少.
方法二:设安排m辆A货车,则安排辆B货车,
w=500m+400×=﹣m+,
∵=9.5,
∴0<m<10,
∵m,都为整数,
∴m=2,5,8,
故符合题意的运输方案有三种:
①A货车2辆,B货车10辆;
②A货车5辆,B货车6辆;
③A货车8辆,B货车2辆;
∵﹣<0.
∴w随m的增大而减小,
∴费用越少,m越大,
故方案③费用最少.
23.(8分)如图,在四边形ABCD中,AB∥CD,BD交AC于G,E是BD的中点,连接AE并延长,交CD于点F,F恰好是CD的中点.
(1)求的值;
(2)若CE=EB,求证:四边形ABCF是矩形.
【分析】(1)首先证明AB=CF=DF,再证明△ABG∽△CDG即可解决问题;
(2)根据有一个角是直角的平行四边形是矩形即可证明;
【解答】(1)解:∵AB∥CD,
∴∠ABE=∠EDC.
∵∠BEA=∠DEF,BE=DE,
∴△ABE≌△FDE(ASA).
∴AB=DF.
∵F是CD的中点,
∴CF=FD.
∴CD=2AB.
∵∠ABE=∠EDC,∠AGB=∠CGD,
∴△ABG∽△CDG.
∴.
(2)证明:∵AB∥CF,AB=CF,
∴四边形ABCF是平行四边形.
∵CE=BE,BE=DE,
∴CE=ED.
∵CF=FD,
∴EF垂直平分CD.
∴∠CFA=90°.
∴四边形ABCF是矩形.
五、解答题(三)(每小题10分,共20分)
24.(10分)如图,⊙O是△ABC的外接圆,AB为直径,点P为⊙O外一点,且PA=PC=AB,连接PO交AC于点D,延长PO交⊙O于点F.
(1)证明:=;
(2)若tan∠ABC=2,证明:PA是⊙O的切线;
(3)在(2)条件下,连接PB交⊙O于点E,连接DE,若BC=2,求DE的长.
【分析】(1)首先证明PF垂直平分线段AC,利用垂径定理可得结论.
(2)设BC=a,通过计算证明AD2=PD•OD,推出△ADP∽ODA即可解决问题.
(3)法一:如图,过点E作EJ⊥PF于J,BK⊥PF于K.想办法求出EJ,DJ即可解决问题.
法二:由△PEA∽△PAB,推出=,推出PE=4,想办法求出EJ,DJ即可解决问题.
【解答】(1)证明:连接OC.
∵PC=PA,OC=OA,
∴OP垂直平分线段AC,
∴=.
(2)证明:设BC=a,
∵AB是直径,
∴∠ACB=90°,
∵tan∠ABC==2,
∴AC=2a,AB===3a,
∴OC=OA=OB=,CD=AD=a,
∵PA=PC=AB,
∴PA=PC=3a,
∵∠PDC=90°,
∴PD===4a,
∵DC=DA,AO=OB,
∴OD=BC=a,
∴AD2=PD•OD,
∴=,
∵∠ADP=∠ADO=90°,
∴△ADP∽△ODA,
∴∠PAD=∠DOA,
∵∠DOA+∠DAO=90°,
∴∠PAD+∠DAO=90°,
∴∠PAO=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(3)解:法一:如图,过点E作EJ⊥PF于J,BK⊥PF于K.
∵BC=2,
由(2)可知,PA=6,AB=6,
∵∠PAB=90°,
∴PB===6,
∵PA2=PE•PB,
∴PE==4,
∵∠CDK=∠BKD=∠BCD=90°,
∴四边形CDKB是矩形,
∴CD=BK=2,BC=DK=2,
∵PD=8,
∴PK=10,
∵EJ∥BK,
∴==,
∴==,
∴EJ=,PJ=,
∴DJ=PD﹣PJ=8﹣=,
∴DE===.
法二:由(2)可得BC=2,AC=4,AB=6,PA=6,PB=6,
在Rt△PBA中,连接AE,可得∠AEB=90°,
∴∠PEA=∠PAB=90°,又∠APE=∠APB,
∴△PEA∽△PAB,
∴=,
∴PE=4,
过E作EJ⊥PD于J,过B作BK⊥PF于K,如图所示,
∴∠BCD=∠CDF=∠BKD=90°,
∴四边形BCDK是矩形,
∴BK=CD=2,
在Rt△BPH中,sin∠BPH==,
在Rt△PEN中,sin∠BPH=,
∴EJ=,
∴PJ==,
∴JD=PD﹣PJ=,
在Rt△JED中,DE==.
25.(10分)在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记△BDE的面积为S1,△ABE的面积为S2,求的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点.试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【分析】(1)设抛物线的解析式为y=a(x﹣1)(x﹣4),将点C的坐标代入可求得a的值,从而得到抛物线的解析式;
(2)过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K,证明△AKE∽△DFE,得出,则,求出直线BC的解析式为y=x﹣2,设D(m,m﹣2),则F(m,m﹣2),可得出的关系式,由二次函数的性质可得出结论;
(3)设P(a1,),①当点P在直线BQ右侧时,如图2,过点P作PN⊥x轴于点N,过点Q作QM⊥直线PN于点M,得出Q(a1,a1﹣2),将点Q的坐标代入抛物线的解析式求得a的值即可,②当点P在直线BQ左侧时,由①的方法同理可得点Q的坐标为(a1,2),代入抛物线的解析可得出答案.
【解答】解:(1)设抛物线的解析式为y=a(x+1)(x﹣4).
∵将C(0,﹣2)代入得:4a=2,解得a=,
∴抛物线的解析式为y=(x+1)(x﹣4),即y=x2﹣x﹣2.
(2)过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K,
∴AK∥DG,
∴△AKE∽△DFE,
∴,
∴,
设直线BC的解析式为y=kx+b1,
∴,解得,
∴直线BC的解析式为y=x﹣2,
∵A(﹣1,0),
∴y=﹣﹣2=﹣,
∴AK=,
设D(m,m﹣2),则F(m,m﹣2),
∴DF=m+2=﹣+2m.
∴m=﹣.
∴当m=2时,有最大值,最大值是.
(3)存在.符合条件的点P的坐标为()或().
∵l∥BC,
∴直线l的解析式为y=x,
设P(a1,),
①当点P在直线BQ右侧时,如图2,过点P作PN⊥x轴于点N,过点Q作QM⊥直线PN于点M,
∵A(﹣1,0),C(0,﹣2),B(4,0),
∴AC=,AB=5,BC=2,
∵AC2+BC2=AB2,
∴∠ACB=90°,
∵△PQB∽△CAB,
∴,
∵∠QMP=∠BNP=90°,
∴∠MQP+∠MPQ=90°,∠MPQ+∠BPN=90°,
∴∠MQP=∠BPN,
∴△QPM∽△PBN,
∴=,
∴QM=,PM=(a1﹣4)=a1﹣2,
∴MN=a1﹣2,BN﹣QM=a1﹣4﹣=a1﹣4,
∴Q(a1,a1﹣2),
将点Q的坐标代入抛物线的解析式得﹣2=a1﹣2,
解得a1=0(舍去)或a1=.
∴P().
②当点P在直线BQ左侧时,
由①的方法同理可得点Q的坐标为(a1,2).
此时点P的坐标为().
相关试卷
这是一份2022-2023学年广东省东莞市宏远外国语学校八年级(下)期中数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2023年广东省东莞市宏远外国语学校中考数学一模试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年广东省广州外国语学校中考数学一模试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









