吉林省松原市乾安县2022-2023学年八年级下学期5月期中数学试题

这是一份吉林省松原市乾安县2022-2023学年八年级下学期5月期中数学试题，共15页。
数学试题共8页，包括六道大题，共26道小题。全卷满分120分。考试时间为120分钟。注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内。2.答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿
纸、试题上答题无效。
一、选择题（本大题共6小题，每小题2分，共12分）
1. 下列各式是最简二次根式的是（ ）
A. B. C. D.
2. 下列运算，结果正确的是（ ）
A． B． C． D．
3.如图，某公园处有一块长方形草坪，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们踩伤草坪，仅仅少走了（ ）
A. B. C. D.
6题图
5题图
4题图
3题图
4.如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米.如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（ ）( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
5. 在下列四个选项中，能判定四边形ABCD是平行四边形的是（ ）
A．AB＝CD，AD∥BC B．AB∥DC，∠A＝∠B
C．AB∥DC，AD＝BCD．AB∥DC，AB＝DC
6．如图，在正方形中，，点，分别在边，上，．
若将四边形沿折叠，点B恰好落在边上点处，则的长度为（ ）
A. 1B. C. D. 2
八年级数学试卷 第1 页（共8页）
二、填空题（本大题共8小题，每小题3分，共24分）
7. 若式子在实数范围内有意义，则x的取值范围是__________.
8. 计算=___________．
9. 如图，菱形中，对角线与相交于点，若，，则 的长为_________cm．

11题图
9题图
10题图
10.如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，分别连结AB、AD、CD．则四边形ABCD是平行四边形，其依据是___________．
11.在一次综合实践活动中，老师让同学们测量公园里凉亭A，B之间的距离(A，B之间有水池，无法直接测量).智慧小组的同学们在公园里选了凉亭C，D，测AD=CD=10m，∠D=90°，BC=40m，∠DCB=135°，则A，B之间的距离为_______．
12. 如图，在平面直角坐标系xOy中，矩形OABC的顶点A，C的坐标分别是（4，-2），
（1，2），点B在x轴上，则点B的横坐标是________．
13题图
12题图
14题图
13.如图所示，在△ABC中，AD⊥BC于点D,E、F分别是AB、AC边的中点，连接DE、EF、FD,当△ABC满足条件_______时，四边形AEDF是菱形.(填一个你认为恰当的条件即可)
八年级数学试卷 第2页（共8页）
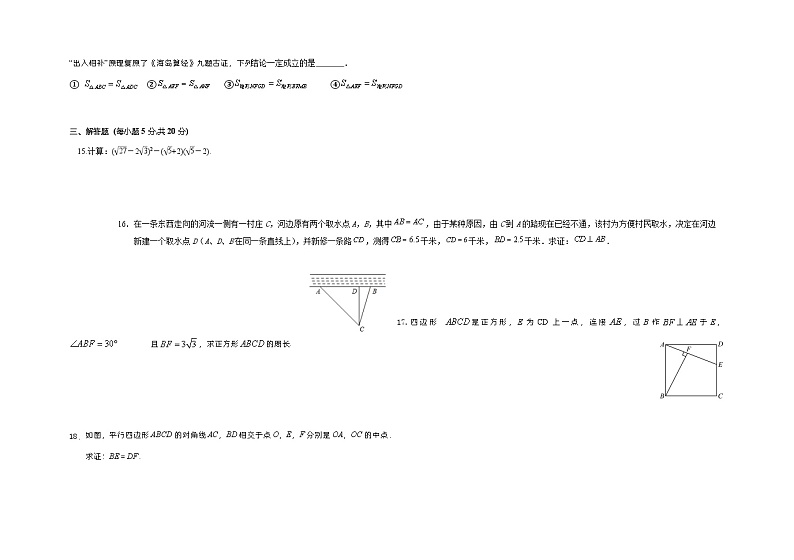
14.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证，下列结论一定成立的是 ．
= 1 \* GB3 \* MERGEFORMAT ① = 2 \* GB3 \* MERGEFORMAT ② = 3 \* GB3 \* MERGEFORMAT ③ = 4 \* GB3 \* MERGEFORMAT ④
三、解答题 (每小题5分,共20分)
15.计算：( eq \r(27) －2 eq \r(3) )2－( eq \r(5) +2)( eq \r(5) －2).
16．在一条东西走向的河流一侧有一村庄C，河边原有两个取水点A，B，其中，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水，决定在河边新建一个取水点D（A、D、B在同一条直线上），并新修一条路，测得千米，千米，千米．求证：.
17.四边形 是正方形，E为CD上一点，连接，过B作于E， 且，求正方形的周长.
如图，平行四边形ABCD的对角线AC，BD相交于点O，E，F分别是OA，OC的中点．
求证：BE＝DF．
八年级数学试卷 第3页（共8页）
八年级数学试卷 第4页（共8页）
四、解答题 (每小题7分，共28分)
19. 如图，正方形网格中的每个小正方形的边长都是1，每个顶点叫做格点．
（1）在图（1）中以格点为顶点画一个面积为5的正方形；
（2）在图（2）中以格点为顶点画一个三角形，使三角形三边长分别为2，，；
这个三角形的面积为 ．
20.阅读下列一段文字：在平面直角坐标系中，已知两点的坐标是M（x1，y1），N（x2，y2），M、N两点之间的距离可以用公式MN＝计算．解答下列问题：
（1）若点P（2，4），Q（﹣3，﹣8），求P，Q两点间的距离；
（2）若点A（1，2），B（4，﹣2），点O是坐标原点，判断△AOB是什么三角形，并说明理由．
八年级数学试卷 第4页（共8页）
如图，平行四边形ABCD的对角线交于点O，以OD，CD为邻边作平行四边形DOEC，
OE交BC于点F，连结BE．
（1）求证：F为BC中点；
（2）若OB⊥AC，OF＝2，求平行四边形ABCD的周长．
22. 小惠自编一题：“如图，在四边形中，对角线，交于点O，，，求证：四边形是菱形”，并将自己的证明过程与同学小洁交流．

若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．
八年级数学试卷 第5页 （共8页）
五、解答题 (每小题8分，共16分)
23. 如图，在矩形ABCD中，作对角线BD的垂直平分线，交AD于点M，交BC于点N，连接BM、DN
（1）求证：四边形BMDN是菱形；
（2）若矩形ABCD的边长AD＝8，AB＝4，求菱形BMDN的边长．
24．阅读下列解题过程
例：若代数式的值是，求的取值范围．
解：原式=
当时，原式，解得 (舍去)；
当时，原式，符合条件；
当时，原式，解得 (舍去)．
所以，的取值范围是
上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题：
当时，化简： ;
若等式成立，则的取值范围是 ;
若，求的值．
八年级数学试卷 第6页 （共8页）
六、解答题 (每小题10分，共20分)
25．如图，在中，∠B=90°，，．点从点出发沿方向以每秒个单位长的速度向点A匀速运动，同时点从点出发沿方向以每秒个单位长的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点运动的时间是秒．过点作于点，连接DE、EF．
（1）求长；
（2）求证：；
（3）当为何值时，为直角三角形？请说明理由．
八年级数学试卷 第7页 （共8页）
26.综合与实践
综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动.
（1）操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM.
根据以上操作，当点M在EF上时，写出图1中一个30°的角： ；
（2）迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（I）中的方式操作，并延长PM交CD于点Q，连接BQ.
①如图2，当点M在EF上时，∠MBQ= ，∠CBQ= ；
②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由.
（3）拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ=1cm时，直接写出AP的长．
八年级数学试卷 第8页 （共8页）
\
乾安县2022—2023学年度第二学期期中质量检测
八年级数学试题参考答案及评分标准
（请老师在阅卷前自做一遍答案）
单项选择题（每小题2分，共12分）
1.B 2.D 3.A 4.C 5. D 6.D
二、填空题（每小题3分，共24分）
7. ；8. ； 9. 8 10.两组对边分别相等的四边形是平行四边形； 11. ；
12. 5 ；13. AB＝AC(或∠B＝∠C或BD＝DC,答案不唯一)； 14. ①②③
三、解答题（每小题5分，共20分）
15.解：(－2)2－(+2)(－2)
＝27－36+12－(5－4)＝27－36+12－1＝2.………5分
证明：由题知，CD=6,BC=6.5
在三角形BCD中，BD2+CD2=BC2 ………2分 ∴三角形BCD是直角三角形，………3分
∠CDB=90°………4分∴CD⊥AB，…5分
17. 解：∵ ∴．………1分 ∵，∴．………2分
∵，∴，………3分
∴（负值舍去），………4分 ∴正方形的周长为．分
18.证明：∵四边形ABCD是平行四边形∴AB∥CD，OC＝OA，………1分
CD＝AB∴∠DCF＝∠BAE………2分
∵E，F分别是OA，OC的中点∴CF＝OC，AE＝OA
∴CF＝ AE………3分
在△DCF和△BAE中
∴△DCF≌△BAE（SAS）………4分 ∴DF＝BE．……5分
四、解答题（每小题7分，共28分）
19.解：（1）如图所示即为所求面积为5的正方形∵，∴如图所示即的正方形即为所求；………3分
（2）如图所示，∵，，∴如图所示三角形即所求；………6分
这个三角形的面积为，故答案：2．………7分
解：(1)P，Q两点间距离＝＝13；
……3分
△AOB是直角三角形，……4分
理由如下：AO2＝(1﹣0)2+(2﹣0)2＝5，BO2＝(4﹣0)2+(﹣2﹣0)2＝20，AB2＝(4﹣1)2+(﹣2﹣2)2＝25
则AO2+BO2＝AB2，……6分 ∴△AOB是直角三角形．分
（1）证明：∵四边形ABCD是平行四边形，∴OB＝OD，……1分
∵四边形DOEC为平行四边形，，，……2分
，，∴四边形OBEC为平行四边形，……3分
，即F是BC的中点．……4分
（2）∵四边形ABCD是平行四边形，，是菱形，……5分
∵四边形OBEC为平行四边形，，是矩形，，……6分
，，的周长．分
赞成小洁的说法……1分 补充：．……2分
证明：，，，．……4分
又∵．∴，……6分
∴四边形是菱形．……7分
五、解答题（每小题8分，共16分）
23. （1）证明：∵矩形ABCD，∴OB＝OD，MD∥BN，……1分
∴∠MDO＝∠NBO，……2分∵∠DOM＝∠BNO，
∴△MDO≌△NBO（ASA），∴MD＝NB，……3分
∴四边形MDNB是平行四边形，∵BD⊥MN，
∴四边形MDNB是菱形；……4分
由（1）可知DM＝BM，在Rt△ABM中，∵BM2＝AM2+AB2，∴BM2＝（AD﹣DM）2+AB2，……5分
∴BM2＝（AD﹣BM）2+AB2 ……6分 ∵AD＝8，AB＝4，， 解得BM＝5，……7分
∴ 菱形BMDN的边长为5．……8分
24.（1）解：当时，
原式===……2分


（2）原式=
当时，原式，解得(舍去)；
当时，原式，符合条件；
当时，原式，解得 (舍去)．
所以，的取值范围是；……4分

（3）原式=
当时，原式，解得符合条件；……5分

当时，原式，此方程无解，不符合条件；……6分

当时，原式，解得 符合条件．……7分

所以，的值是或．………8分
六、解答题（每小题10分，共20分）
25.解：（1）设，，，．
由勾股定理得，，解得：，………2分 ………4分
（2）证明：由题意得，CD=2t，则，………5分
在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴．………6分
又，；………7分
（3）解：当秒或秒时，为直角三角形，理由如下：
分情况讨论：
①∠EDF=∠DFC=90°时，则，∴∠AED=∠B=90°，∠ADE=∠C=30°，
∴AD=2AE，∴10-2t=2t， ∴；………8分
②∠DEF=90°时，∵AB⊥BC，DF⊥BC，∴．又∵AE=DF，
∴四边形AEFD为平行四边形，∴，AE∥DF，∴∠ADE=∠DEF=60°，∴∠AED=30°，
∴，∴，∴；………9分
③∠EFD=90°时，此种情况不存在．当秒或秒时，为直角三角形．………10分
26.解：（1）∠ABP或∠PBM或∠MBC或∠BME（注：任意写出一个即可）………2分
（2）①15,15………4分
②∠MBQ=∠CBQ(注：若没写出完判断结果，但后续证明正确，不扣分）………5分
理由如下：
∵四边形ABCD是正方形，∴AB=BC，∠A=∠C=90°,
由轴对称性质可知，BM=AB，∠BMP=∠A=90°
∠BMQ=∠C=90°BM=BC
∵BQ是公共边，∴Rt△MBQ≌Rt△CBQ………7分

∴∠MBQ=∠CBQ………8分

(3) cm 或 cm



此答案仅供参考，若有其它正确做法正常给分！