人教版七年级下册第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质教课课件ppt

这是一份人教版七年级下册第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质教课课件ppt，共35页。PPT课件主要包含了知识精讲，典例解析，知识拓展，精典例题，小试牛刀，归纳整理，谈谈你的收获吧等内容，欢迎下载使用。

9.1 不等式的性质第1课时 不等式的性质
第七章 平面直角坐标系
1.理解并掌握不等式的基本性质;2.通过实例操作,培养学生观察、分析、比较问题的能力, 会用不等式的基本性质解简单的不等式.(重点、难点)
由a+2=b+2, 能得到a=b？
由0.5a=0.5b, 能得到a=b？
由 -2a= -2b, 能得到a=b？
由a-2=b-2, 能得到a=b？
目标导学一：不等式的性质1
等式基本性质1：等式的两边都加上（或减去）同一个数或式子，等式仍旧成立
等式基本性质2：等式的两边都乘以（或除以）同一个不为0的数，等式仍旧成立
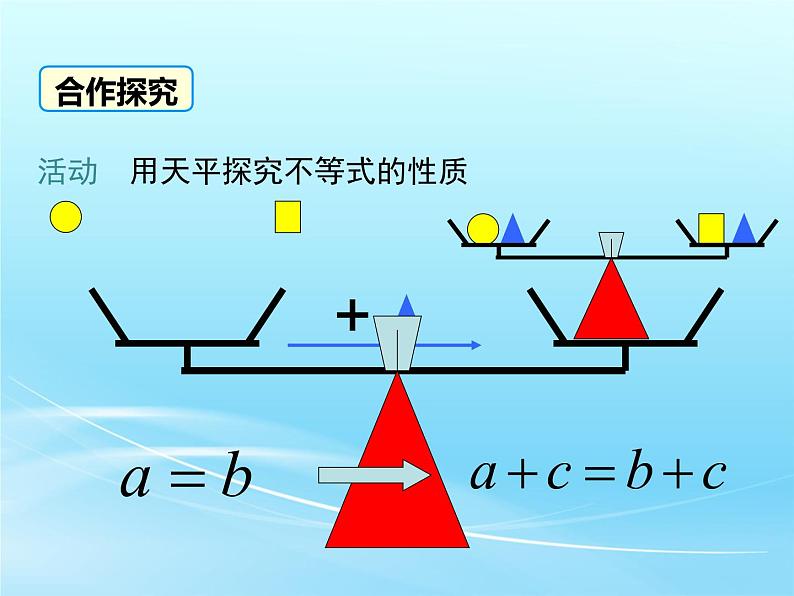
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 （c≠0），
活动 用天平探究不等式的性质
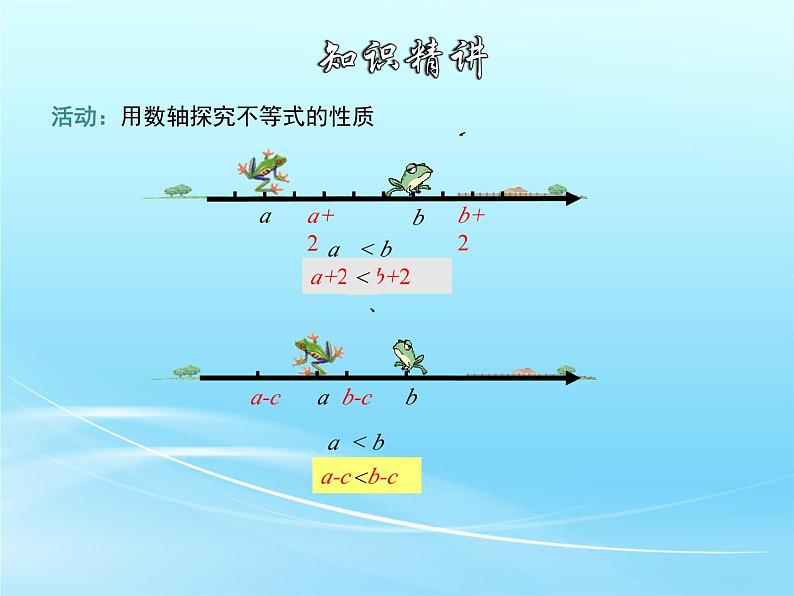
活动：用数轴探究不等式的性质
不等式基本性质1：不等式的两边都加上（或减去）同一个数或式子，
如果____,那么_________.
解： 因为 a>b，两边都加上3，
因为 a 由不等式基本性质1，得
a+3 > b+3；
由不等式基本性质1，得
a-5 < b-5 .
（1）已知 a>b，则a+3 b+3
（2）已知 a例1：用“>”或“<”填空：
⑴ 6＞2 6×5 2×5 6×(-5) 2×(-5)⑵ -2＜3 (-2)×6 3×6 (-2)×(-6) 3×(-6)⑶ 8＞(-6) 8÷2 (-6)÷2 8÷(-2) (-6)÷(-2)
不等式两边都乘(或除以)同一个
目标导学二：不等式的基本性质2、3
不等式基本性质2 不等式的两边都乘（或除以）同一个正数，不等号的方向不变.
a-a-b>b-a-b
不等式两边同乘以-1，不等号方向改变.
猜想：不等式两边同乘以一个负数，不等号方向改变.
不等式基本性质3 不等式的两边都乘（或除以）同一个负数，不等号的方向改变.
不等式性质1： 不等式两边同时加上( 或减去 )同一个整式，不等号的方向不变。不等式性质2： 不等式两边同时乘以( 或除以 )同一个正数，不等号的方向不变。不等式性质3： 不等式两边乘( 或除以 )同一个负数，不等号的方向改变。
思考: 等式有对称性及传递性，那么不等式具有对称性和传递性吗?
已知x>5,那么5由8如：8<10，10<15 ，8 15.
x>5 5性质（对称性）:如果a>b,那么b性质（同向传递性）:如果a>b,b>c,那么a>c.
例2. 设a＞b，用“＜”或“＞”填空并口答是根据哪一条不等式基本性质。
（1）a - 3____b - 3； （2）a÷3____b÷3 （3） ; (4) -4a____-4b (5) 2a+3____2b+3; (6) (m2+1) a ____ (m2+1)b (m为常数)
若m>n，判断下列不等式是否正确：（1）m-7-5n （ ）（4） ( )（5） m+5≥n+5 ( )
例3.将下列不等式化成x > a或 x < a 的形式
(1) x-5 > -1
(2) -2x > 4
(3) 7x < 6x －6
解:根据不等式的基本性质1,不等式两边都加上5得x > 4
解:根据不等式的基本性质3 , 不等式两边都除以-2得, x < －2
解:根据不等式的基本性质1,不等式两边都减去6x,得x < －6
小结：在利用不等式的基本性质进行变形时，当不等式的两边都乘以(或除以)同一个字母，字母代表什么数是问题的关键，这决定了是用不等式基本性质2还是基本性质3，也就是不等号是否要改变方向的问题
实数a，b，c在数轴上的位置如图，则下列不等关系正确的是（ ）. A.ab>bc B.ac>bc C.ac>ab D. ab>ac.
例4
例5
如果t>0，那么a+ t与a的大小关系是（ ）.A.a+t>a B.a+t例6
若已知关于x的不等式(1-a)x >2变形后得到 成立，则a应满足的条件是（ ） A.a>0 B.a>1 C.a<0 D. a<1.
把(1-a)看作一个整体
(1) ∵ 2a < 3a , ∴a是____数
(3) ∵ ax < a 且 x > 1 , ∴a是____数
(2) ∵ , ∴a是____数
等式性质与不等式性质的区别和联系
区别：等式两边都乘以（或除以）同一个数（除数不为0）时，结果仍相等；不等式两边都乘以（或除以）同一个数（除数不为0）时，会出现两种情况，若是正数，不等号方向不改变，若是负数不等号方向要改变，而且不等式两边同乘以0，结果相等.联系：不等式性质和等式性质都讨论的是两边都加上或减去同一个数的情况和两边都乘以或除以同一个数（除数不为0）的情况，即研究“形式”一致.
例7 利用不等式的性质解下列不等式： (1) x-7＞26； (2) 3x<2x+1； 　　　
化为x＞a或x﹤a的形式
方法：不等式基本性质1~3
目标导学三：利用不等式的性质解简单的不等式
下面是某同学根据不等式的性质做的一道题：
在不等式-4x+5>9的两边都减去5，得
-4x > 4
在不等式-4x> 4的两边都除以-4，得
x > -1
请问他做对了吗？如果不对，请改正.
应用性质对不等式简单变形
如果a>b，那么a+c>b+c，a-c>b-c
1.若k<0,则下列不等式中不成立的是( ) A.k+2>k-2 　B.-6k>0 C.k>-k D.k<-k
2.已知a3. 判断下列各题的推导是否正确？为什么？(1)因为7.5＞5.7，所以-7.5＜-5.7；(2)因为a+8＞4，所以a＞-4；(3)因为4a＞4b，所以a＞b；(4)因为-1＞-2，所以-a-1＞-a-2；(5)因为3＞2，所以3a＞2a．
(1)正确，根据不等式基本性质3．
(2)正确，根据不等式基本性质1．
(3)正确，根据不等式基本性质2．
(4)正确，根据不等式基本性质1．
(5)不对，应分情况逐一讨论．当a＞0时，3a＞2a．(不等式基本性质2)当 a=0时，3a=2a．当a＜0时，3a＜2a．(不等式基本性质3)
4.选择适当的不等号填空：
（1)∵0 1,∴ a a+1(不等式的基本性质1）；（2）∵(a-1)2 0, 　∴(a-1)2-2 -2(不等式的基本性质1）(3)若x+1＞0,两边同加上-1,得____________(依据:_____________________).(4)若2 x ＞-6,两边同除以2,得________,依据_______________.(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
5.利用不等式的性质解下列不等式,并在数轴上表示其解集．
(2)-2x > 3
(1)x-5 > -1
(3)7x < 6x-6
作 业 ：1.完成同步练习题2.背诵知识点