湖南省常德市2021-2022学年高一下学期期末数学试题（原卷及解析版）

这是一份湖南省常德市2021-2022学年高一下学期期末数学试题（原卷及解析版），文件包含精品解析湖南省常德市2021-2022学年高一下学期期末数学试题解析版docx、精品解析湖南省常德市2021-2022学年高一下学期期末数学试题原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
2021~2022学年度常德市高一年级质量检测考试数 学（试题卷）试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，时量120分钟．注意事项：1． 所有试题的答案请在答题卡的指定区域内作答．2． 考试结来后，只交答题卡．第I卷（选择题，共60分）一、单选题（本大题共计8个小题，每小题5分，共计40分）1. 已知集合，则（    ）A. {－1，0，1} B. {0，1} C.  D. 2. 已知且，则最大值等于A.  B.  C.  D. 3. 已知复数，其中是虚数单位，则复数|z|等于（    ）A. 3 B. 2 C. 10 D. 4. 如图所示，在长方形ABCD中，设又，则（    ）
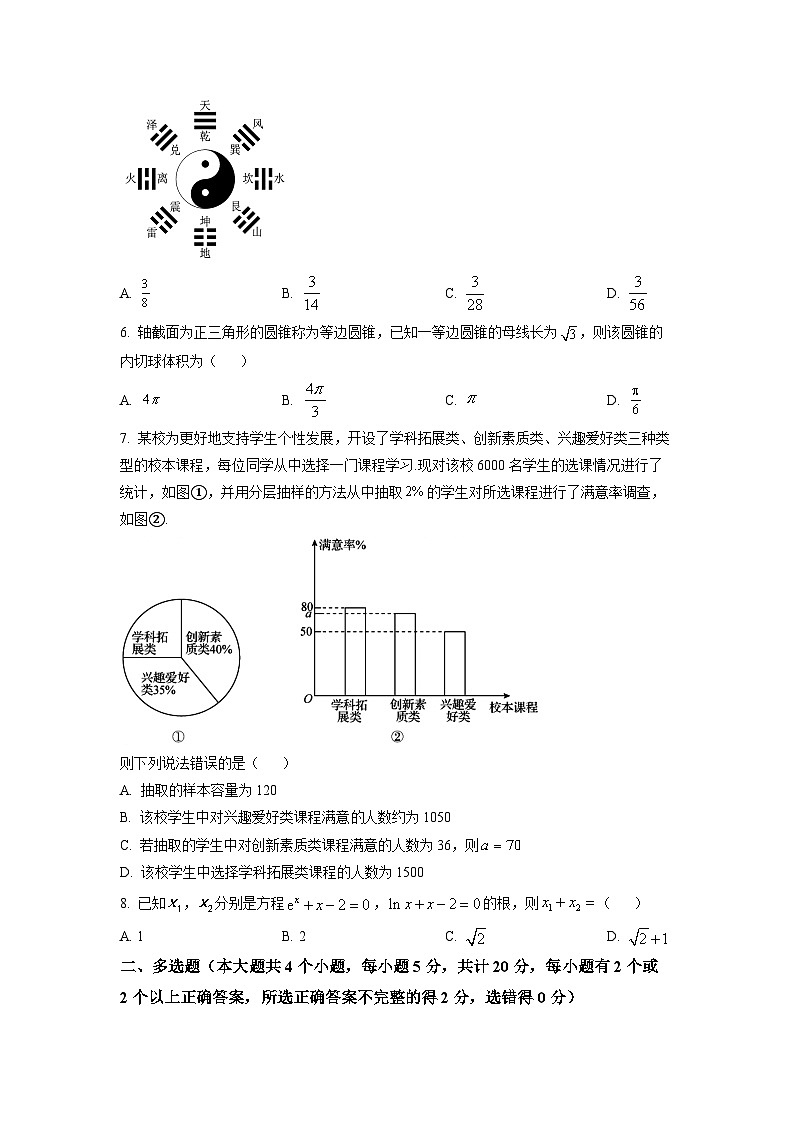
 A.  B. － C. 1 D. 5. 《易经》是中国文化中的精髓，如图是易经八卦图（含乾、坤、巽、震、坎、离、艮、兑八卦），每一卦由三根线组成（表示一根阳线， 表示一根阴线），从八卦中任取两卦，这两卦中阳线之和为的概率（    ）A.  B.  C.  D. 6. 轴截面为正三角形的圆锥称为等边圆锥，已知一等边圆锥的母线长为，则该圆锥的内切球体积为（    ）A.  B.  C.  D. 7. 某校为更好地支持学生个性发展，开设了学科拓展类、创新素质类、兴趣爱好类三种类型的校本课程，每位同学从中选择一门课程学习.现对该校6000名学生的选课情况进行了统计，如图①，并用分层抽样的方法从中抽取的学生对所选课程进行了满意率调查，如图②.则下列说法错误的是（    ）A. 抽取的样本容量为120B. 该校学生中对兴趣爱好类课程满意人数约为1050C. 若抽取的学生中对创新素质类课程满意的人数为36，则D. 该校学生中选择学科拓展类课程的人数为15008. 已知，分别是方程，的根，则（    ）A. 1 B. 2 C.  D. 二、多选题（本大题共4个小题，每小题5分，共计20分，每小题有2个或2个以上正确答案，所选正确答案不完整的得2分，选错得0分）9. 下列说法正确的是（    ）A. B. 是的充分不必要条件C. 已知函数的零点为1D. 若的定义域为[0，2]，则的定义域为[－1，1]10. 下列四个命题中错误的是（    ）A. 若事件A，B相互独立，则满足B. 若事件A，B，C两两独立，则C. 若事件A，B，C彼此互斥，则D. 若事件A，B满足，则A，B是对立事件11. 已知函数（其中，，）的部分图象如图所示，则下列结论正确的是（    ）
 A. 函数f(x)的图象的周期为B. 函数f(x)的图象关于点（，0）对称C. 函数f(x)在区间[－，]上的最大值为2D. 直线与）图像所有交点的横坐标之和为12. 如图，在直三棱柱中，，P为线段上的动点，则下列结论中正确的是（    ）A. 点A到平面的距离为B. 平面与底面ABC的交线平行于C. 三棱柱的外接球的表面积为D. 二面角的大小为三、填空题（本大题共4小题，每小题5分，共计20分，要求答案写成最简形式）13. 已知函数f(x)为奇函数，当时，，则___．14. 设，，，若A，B，C三点构成以角B为90°的直角三角形，则实数m的值为___．15. 在△ABC中，A，B，C的对边分别为a，b，c，已知，，且，则△ABC的面积为___．16. 定义在R上的奇函数和偶函数满足，当时，恒成立，则实数k的取值范围______．四、解答题（本大题共计6小题，记70分）17. （1）计算的值．（2）已知，求tan值．      18. 常德市汉寿县新建的野生动物园，声名远播，“五一”假期入园游客近16万人次，目前已建成的一期项目分为猛兽区、食草区、灵长类、大象馆、鳄鱼馆、鸟语林等52个馆舍，入园物种有150多种约3500头（羽）．现在汉寿县的野生动物园已成为省内外游客旅游的目的地．为了了解游客的参观体验的满意度，从游客中随机抽取若干游客进行评分（满分为100分），并统计他们参观馆舍个数情况，根据调查数据制成如下频率分布直方图和频数表．已知评分在[70，90]的游客有11人．参观馆舍数频数10 130335440645250t521 （1）求频率分布直方图和频数分布表中未知量a，t的值；（2）从频率分布直方图中求评分的下四分位数，从频数分布表中求参观馆舍数的80%分位数；（3）规定评分不低于90分为“非常满意”，评分低于60分为“不满意”．现从评分为“非常满意”和“不满意”的游客中任意选取2人评为幸运游客，求评分为“非常满意”和“不满意”的游客恰各一人的概率．  19. 已知在直三棱柱的底面ABC中．，E、F分别为AC和的中点．，D为棱上的动点．（1）请作出过、、E三点截直三棱柱的截面（只要求画出图形，不要求写出做法）（2）证明：（3）当D为的中点时，求直线DE与平面所成的线面角的正切值．  20. 在四边形中，，，，设．（1）当时，求线段的长度；（2）求面积的最大值．    21. 已知二次函数（实数）（1）若的解集为（1，2），求不等式的解集；（2）若对任意，时，恒成立，求的最小值；（3）若对任意，恒成立，求ab最大值．          22. 已知．（1）若时，，求实数k的取值范围；（2）设若方程有三个不同的实数解，求实数k的取值范围．