

初中2 用配方法求解一元二次方程第2课时教案及反思
展开第二章 一元二次方程
2 用配方法求解一元二次方程
第2课时
一、教学目标
1.会用配方法解二次项系数不为1的较复杂的一元二次方程.
2.能够熟练、灵活应用配方法解一元二次方程.
3.进一步经历用配方法解一元二次方程的过程,体会转化的数学的思想.
4.培养学生的数学意识,感受数学学习的价值.
二、教学重难点
重点:用配方法解二次项系数不为1的较复杂的一元二次方程.
难点:熟练、灵活的应用配方法解一元二次方程.
三、教学用具
电脑、多媒体、课件、教学用具等
四、教学过程设计
教学环节 | 教师活动 | 学生活动 | 设计意图 |
环节一 创设情境 | 【回顾】 教师活动:课件出示式子,学生思考后回答. 1.将下列各式填上适当的项,配成完全平方式. (1) x2+2x+____= (x +___)2 (2) x2-4x+____ = (x -___)2 (3) x2+____+36 = (x +___)2 (4) x2 + 10x +___= (x +___)2 (5) x2-x+_____= (x-___)2 预设: (1)12 ,1 (2)22 ,2 (3)12x,6 (4)52,5 (5),.
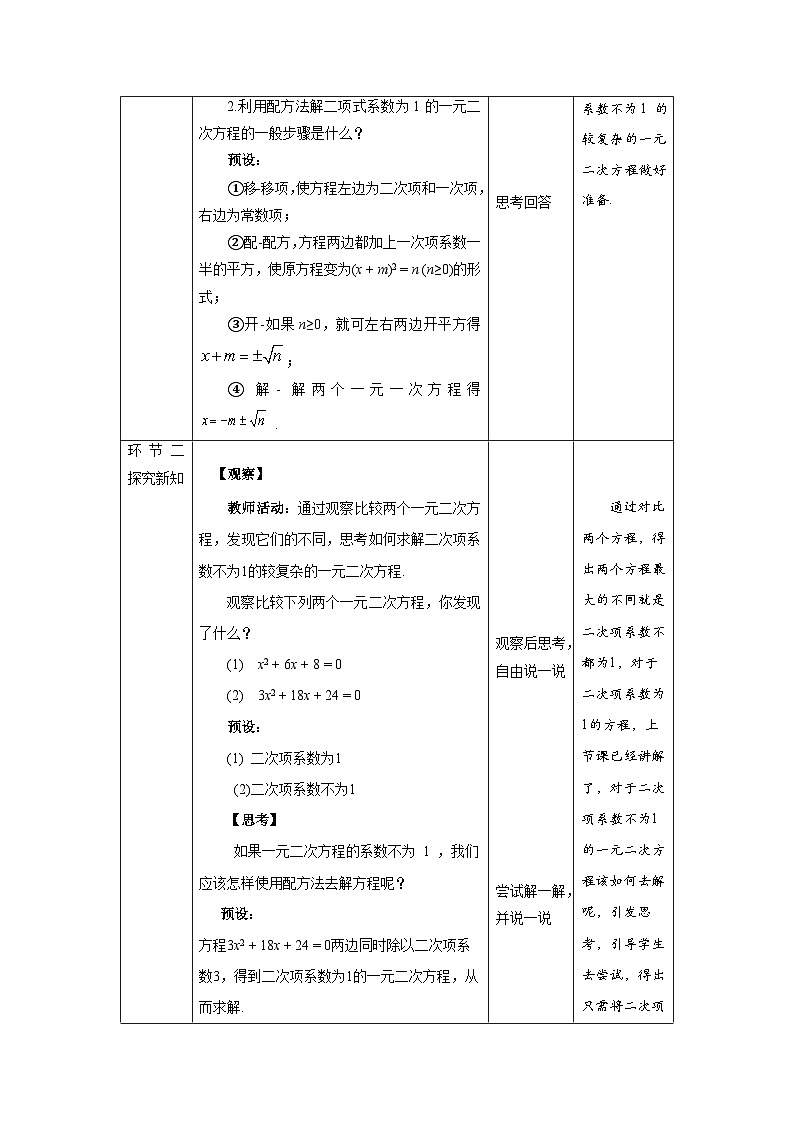
提示:解题关键:常数项是一次项系数一半的平方. 2.利用配方法解二项式系数为1的一元二次方程的一般步骤是什么? 预设: ①移-移项,使方程左边为二次项和一次项,右边为常数项; ②配-配方,方程两边都加上一次项系数一半的平方,使原方程变为(x + m)2 = n (n≥0)的形式; ③开-如果n≥0,就可左右两边开平方得; ④解-解两个一元一次方程得 . |
举手回答
思考回答 |
通过配完全平方式的练习和复习用配方法解一元二次方程的基本步骤,为本课学习解二项式系数不为1 的较复杂的一元二次方程做好准备. |
环节二 探究新知 |
【观察】 教师活动:通过观察比较两个一元二次方程,发现它们的不同,思考如何求解二次项系数不为1的较复杂的一元二次方程. 观察比较下列两个一元二次方程,你发现了什么? (1) x2 + 6x + 8 = 0 (2) 3x2 + 18x + 24 = 0 预设: (1) 二次项系数为1 (2)二次项系数不为1 【思考】 如果一元二次方程的系数不为 1 ,我们应该怎样使用配方法去解方程呢? 预设: 方程3x2 + 18x + 24 = 0两边同时除以二次项系数3,得到二次项系数为1的一元二次方程,从而求解. 归纳:在方程的两边同时除以二次项系数,化二次项系数为1. |
观察后思考,自由说一说
尝试解一解,并说一说 |
通过对比两个方程,得出两个方程最大的不同就是二次项系数不都为1,对于二次项系数为1的方程,上节课已经讲解了,对于二次项系数不为1的一元二次方程该如何去解呢,引发思考,引导学生去尝试,得出只需将二次项系数不为1的转化为二次项系数为1的方程求解即可. |
环节三 应用新知 | 【典型例题】 教师提出问题,学生先独立思考,解答.然后再分小组交流探讨,如遇到有困难的学生适当点拨,最终教师展示答题过程.
例2 解方程 3x2 + 8x -3 = 0 .
分析: ①先两边同除以3:; 思路一:先移项再配方 ②把常数项移到右边: ; ③再两边同时加上一次项系数一半的平.方,得; 即 思路二:先配方再移项 ②再两边同时加上一次项系数一半的平方,得, 即 ; ③把常数项移到右边; ④开平方得:,最后解两个一元一次方程,从而解出一元二次方程的解. 此处只给出思路二的解答过程,PPT两种方式均呈现了. 解:方程两边都除以 3,得 , 配方,得 即 移项,得 两边开平方,得 说一说:用配方法解二次项系数不为1的一元二次方程的一般步骤是什么? 预设:①化—化二次项系数为1 ②配—配方,使原方程变为(x + m)2 - n=0的形式 ③移—移项,使得方程变为(x + m)2 =n的形式 ④开—如果n≥0,就可左右两边开平方得 . ⑤解—解两个一元一次方程得. 【做一做】 教师活动:鼓励学生自主解答,同时提出问题让学生思考. 一小球以 15 m/s 的初速度竖直向上弹出,它在空中的高度 h(m) 与时间 t(s) 满足关系: h = 15t - 5t2,小球何时能达到 10 m 的高度? 预设: 解:根据题意得 15t-5t2 = 10 方程两边都除以 -5,得 t2 -3t = -2 配方,得 即 两边开平方,得 . 请分别描述一下,当t = 1 和t = 2时,小球到达10m所处的运动状态. (动画演示:t = 1 时,小球向上运动,t = 2 时,小球向下运动.) |
明确例题的做法
自由说一说
独立解答,思考回答
|
让学生在探究过程中进一步理解用配方法解二项式系数不为1的一元二次方程的解的基本思路及步骤,培养学生的转化思想.
明确用配方法解二次项系数不为1的一元二次方程的一般步骤.
一方面巩固用配方法解一元二次方程,另一方面借助物理问题,感受学科之间的联系,培养学生分析问题、解决问题的能力. |
环节四 巩固新知 | 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1.解下列方程 (1) 3x2 -9x + 2= 0 ; (2)2x2+6= 7x; (3)4x2 -8x-3= 0; 2.印度古算书中有这样一首诗:“一群猴子分两队,高高兴兴在游戏,八分之一再平方,蹦蹦跳跳树林里;其余十二叽叽喳喳,伶俐活泼又调皮.告我总数有多少,两队猴子在一起?”你能解决这个问题吗? 答案: 1.解: (1) 解:两边同时除以 3,得
配方,得
即 移项,得 两边开平方,得 . (2) 解:两边同时除以 2,得
移项,得 配方,得
即 两边开平方,得
(3) 解:两边同时除以 4,得
配方,得
即 移项,得 两边开平方,得
2.解: 设共有猴子 x 只.根据题意,得方程 整理,得 解得 x1=16,x2=48. 所以,共有猴 16 只或 48 只. |
自主完成练习,然后集体交流评价. |
通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯.
|
环节五 课堂小结 | 思维导图的形式呈现本节课的主要内容:
|
学生尝试回顾本节课所讲的内容 | 通过小结总结回顾本节课学习内容,帮助学生归纳、巩固所学知识. |
环节六 布置作业 | 教科书 第40页 习题2.4 第1、4题
| 学生课后自主完成. | 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整. |
初中数学北师大版九年级上册2 视图第3课时教学设计及反思: 这是一份初中数学北师大版九年级上册2 视图第3课时教学设计及反思,共7页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
初中数学北师大版九年级上册第五章 投影与视图2 视图第2课时教案: 这是一份初中数学北师大版九年级上册第五章 投影与视图2 视图第2课时教案,共7页。教案主要包含了学习目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
初中北师大版1 投影第2课时教学设计及反思: 这是一份初中北师大版1 投影第2课时教学设计及反思,共9页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。













