2022-2023学年福建省泉州市高三下学期3月质量监测（三） 数学（解析版）

泉州市2023届高中毕业班质量监测（三）

2023.03

高 三 数 学

本试卷共22题，满分150分，共8页。考试用时120分钟。

注意事项:

1.答题前，考生先将自己的姓名、准考证号填写在答题卡上。

2.考生作答时，将答案答在答题卡上。请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。在草稿纸、试题卷上答题无效。

3.选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

4.保持答题卡卡面清洁，不折叠、不破损。考试结束后，将本试卷和答题卡一并交回。

一、选择题:本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合A＝{x|-5＜x＜2}，B＝{x||x|＜3}，则AUB＝

A.（- ，2）        B.（-00，3）      C.（-3，2）        D.（-5，3）

2.已知复数z满足（1-i）z＝4i，则z·＝

A.-8                   B.0                       C.8                       D.8i

3.已知α＝0,则cos2α＝

                   B.0                                           

4.某运动员每次射击击中目标的概率均相等，若三次射击中，至少有一次击中目标的概率为，则射击一次，击中目标的概率为

高三数学试题第1页（共8页）

5.已知抛物线C的焦点为F，准线为l，点A在C上，点B在l上.若||＝||＝4， ·（+）＝0，则F到l的距离等于

A.1                             B.2                            C.3                            D.4

6.定义在R上的偶函数f（x）满足f（2-x）+f（x）＝0，且当x∈[0，1]时，f（x），则曲线y＝f（x）在点（，f（）)处的切线方程为

A.4x-4y+11＝0                                            B.4x+4y+11＝0

C.4x-4y+7＝0                                              D.4x+4y+7＝0

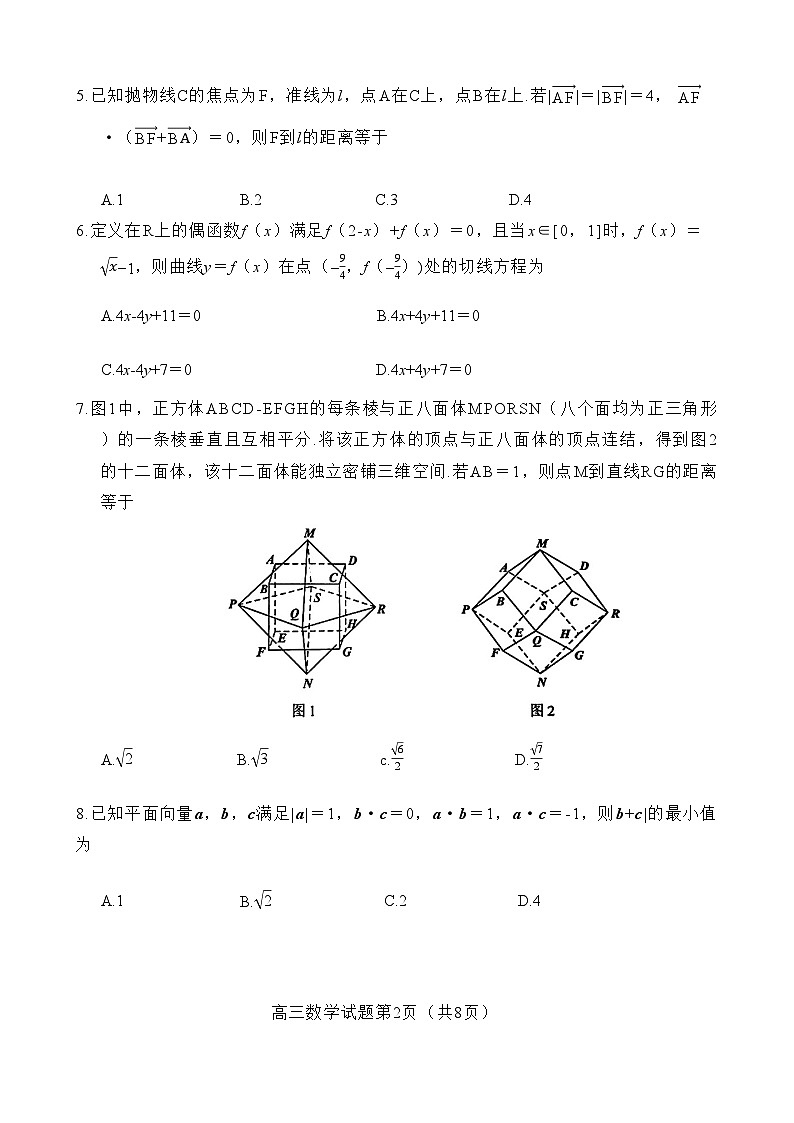
7.图1中，正方体ABCD-EFGH的每条棱与正八面体MPORSN（八个面均为正三角形）的一条棱垂直且互相平分.将该正方体的顶点与正八面体的顶点连结，得到图2的十二面体，该十二面体能独立密铺三维空间.若AB＝1，则点M到直线RG的距离等于

8.已知平面向量a，b，c满足|a|＝1，b·c＝0，a·b＝1，a·c＝-1，则b+c|的最小值为

A.1                                                         C.2                            D.4

高三数学试题第2页（共8页）

二、选择题:本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，有选错的得0分，部分选对的得2分。

9.已知AB为圆C:x2+y2＝4的直径，直线l:y＝k+1与y轴交于点M，则

A.l与C恒有公共点                                         B.△ABM是钝角三角形

C.△ABM的面积的最大值为1                      D.l被C截得的弦的长度的最小值为

10.已知函数f（x）＝sinxcosx，g（x）＝sinx+cosx，则

A.f（x）与g（x）均在（0，）单调递增

B.f（x）的图象可由g（x）的图象平移得到

C.f（x）图象的对称轴均为g（x）图象的对称轴

D.函数y＝f（x）+g（x）的最大值为

11.在长方体ABCD-A1B1C1D1中，AB＝AD＝2，AA1＝1，点P，Q在底面A1B1C1D1内，直线AP与该长方体的每一条棱所成的角都相等，且AP⊥CQ，则

B.点Q的轨迹长度为

C.三棱锥D-A1QB的体积为定值

D.AP与该长方体的每个面所成的角都相等

12.某商场设有电子盲盒机，每个盲盒外观完全相同，规定每个玩家只能用一个账号登陆，且每次只能随机选择一个开启.已知玩家第一次抽盲盒，抽中奖品的概率为，从第二次抽盲盒开始，若前一次没抽中奖品，则这次抽中的概率为，若前一次抽中奖品;则这次抽中的概率为.记玩家第n次抽盲盒，抽中奖品的概率为Pn，则

A.P2                                               B.数列{Pn}为等比数列

C.P                                                 D.当n≥2时，n越大，Pn越小

高三数学试题第3页（共8页）

三、填空题:本题共4小题，每小题5分，共20分。

13.设随机变量X~N（72，2），若P（70＜X＜73）＝0.3，则P（71＜X＜74）＝_____.

14.已知（x+m）6＝a0+a1x+a2x2+a3x3+a4x4+a5x3+a6x6，且a3+a6＝1，则m＝_____.

15.已知函数f（x）＝|ex-1|-ax有两个零点，则实数a的取值范围为_______.

16.已知双曲线C:-＝1（a＞0，b＞0）的左、右焦点分别为F1，F2，C的渐近线与圆x2+y2＝a2在第一象限的交点为M，线段MF2与C交于点N，O为坐标原点.若MF1∥ON，则C的离心率为________.

四、解答题:本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。

17.（10分）

在△ABC中，角A，B，C所对的边分别为a，b，c，（a+c）sinA＝sinA+sinC，

c2+c＝b2-1.

（1）求B；

（2）已知D为AC的中点，，求△ABC的面积.

高三数学试题第4页（共8页）

18.（12分）

已知{an}为等差数列，且an+1＝2an-2n+3.

（1）求{an}的首项和公差;

（2）数列{bn}满足bn＝ 其中k，n∈N*，求.

19.（12分）

如图，三棱台ABC-A1B1C1中，AB＝BC＝2B1C1＝2，D是AC的中点，E是棱BC上的动点.

（1）试确定点E的位置，使AB1∥平面DEC1;

（2）已知AB⊥BC1，CC1⊥平面ABC.设直线BC1与平面DEC1，所成的角为θ，试在（1）的条件下，求cosθ的最小值.

高三数学试题第5页（共8页）

20.（12分）

港珠澳大桥海底隧道是当今世界上埋深最大、综合技术难度最高的沉管隧道，建设过程中突破了许多世界级难题，其建成标志着我国在隧道建设领域已达到世界领先水平.在开挖隧道施工过程中，若隧道拱顶下沉速率过快，无法保证工程施工的安全性，则需及时调整支护参数.某施工队对正在施工的隧道工程进行下沉量监控量测工作，通过对监控量测结果进行回归分析，建立前t天隧道拱顶的累加总下沉量z（单位:毫米）与时间t（单位:天）的回归方程，通过回归方程预测是否需要调整支护参数.已知该隧道拱顶下沉的实测数据如下表所示:

研究人员制作相应散点图，通过观察，拟用函数z＝kebt进行拟合.令u＝lnz，计算得:

（1）请判断是否可以用线性回归模型拟合u与t的关系;（通常|r|>0.75时，认为可以用线性回归模型拟合变量间的关系）

（2）试建立z与t的回归方程，并预测前8天该隧道拱顶的累加总下沉量;

（3）已知当拱顶下沉速率超过9毫米/天，支护系统将超负荷，隧道有塌方风险.若规定每天下午6点为调整支护参数的时间，试估计最迟在第几天需调整支护参数，才能避免塌方.

② 回归直线中斜率和截距的最小二乘估计公式分别为:

③ 参考数据:≈14.5， ln10≈2.30.

高三数学试题第6页（共8页）

21.（12分）

已知椭圆C:＝1的左、右顶点分别为A，B.直线l与C相切，且与圆O:x2+y2＝4交于M，N两点，M在N的左侧.

（1）若|，求l的斜率;

（2）记直线AM，BN的斜率分别为k1，k2，证明:k1k2为定值.

高三数学试题第7页（共8页）

22.（12分）

已知f（x）x2-a（x-1）-xlnx有两个极值点x1，x2，且x1＜x2.

（1）求a的范围;

（2）当0＜a≤1-ln2时，证明:＜f（x1）+f（x2）＜1.

高三数学试题第8页（共8页）