2023年北京市西城区中考二模数学试卷（无答案）

2023年北京市西城区中考二模数学试卷

学校:___________姓名：___________班级：___________考号：___________

一、未知

1．图是某几何体的视图，则该几何体是（　　）

A．长方体 B．三棱柱 C．圆锥 D．正方体

2．据报道，至2022年，我国已经建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系，基本养老保险覆盖10.4亿人，将1040000000用科学记数法表示应为（　　）

A． B． C． D．

3．方程组的解是（　　）

A． B． C． D．

4．比大且比小的整数可以是（　　）

A．1 B．3 C．5 D．7

5．如图，直线，直线EF分别交AB，CD于点E，F，∠BEF的平分线交CD点G，若∠BEF=116°，则∠EGC的大小是（　　）

A．116° B．74° C．64° D．58°

6．一个不透明的口袋中有3个红球和1个白球，这四个球除颜色外完全相同．摇匀后，随机从中摸出一个小球不放回，再随机摸出一个小球，则两次摸出小球的颜色相同的概率是（　　）

A． B． C． D．

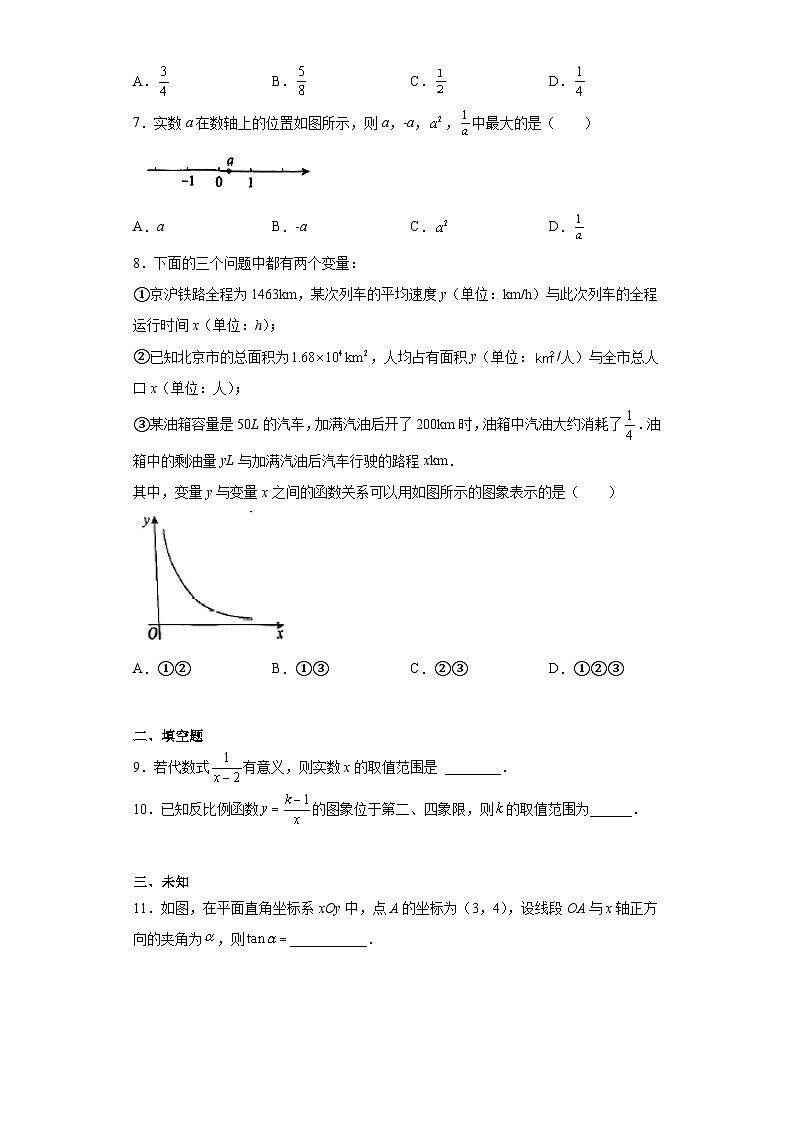
7．实数a在数轴上的位置如图所示，则a，-a，，中最大的是（　　）

A．a B．-а C． D．

8．下面的三个问题中都有两个变量：

①京沪铁路全程为1463km，某次列车的平均速度y（单位：km/h）与此次列车的全程运行时间x（单位：h）；

②已知北京市的总面积为，人均占有面积y（单位：/人）与全市总人口x（单位：人）；

③某油箱容量是50L的汽车，加满汽油后开了200km时，油箱中汽油大约消耗了．油箱中的剩油量yL与加满汽油后汽车行驶的路程xkm．

其中，变量y与变量x之间的函数关系可以用如图所示的图象表示的是（　　）

A．①② B．①③ C．②③ D．①②③

二、填空题

9．若代数式有意义，则实数x的取值范围是 ________．

10．已知反比例函数的图象位于第二、四象限，则的取值范围为______．

三、未知

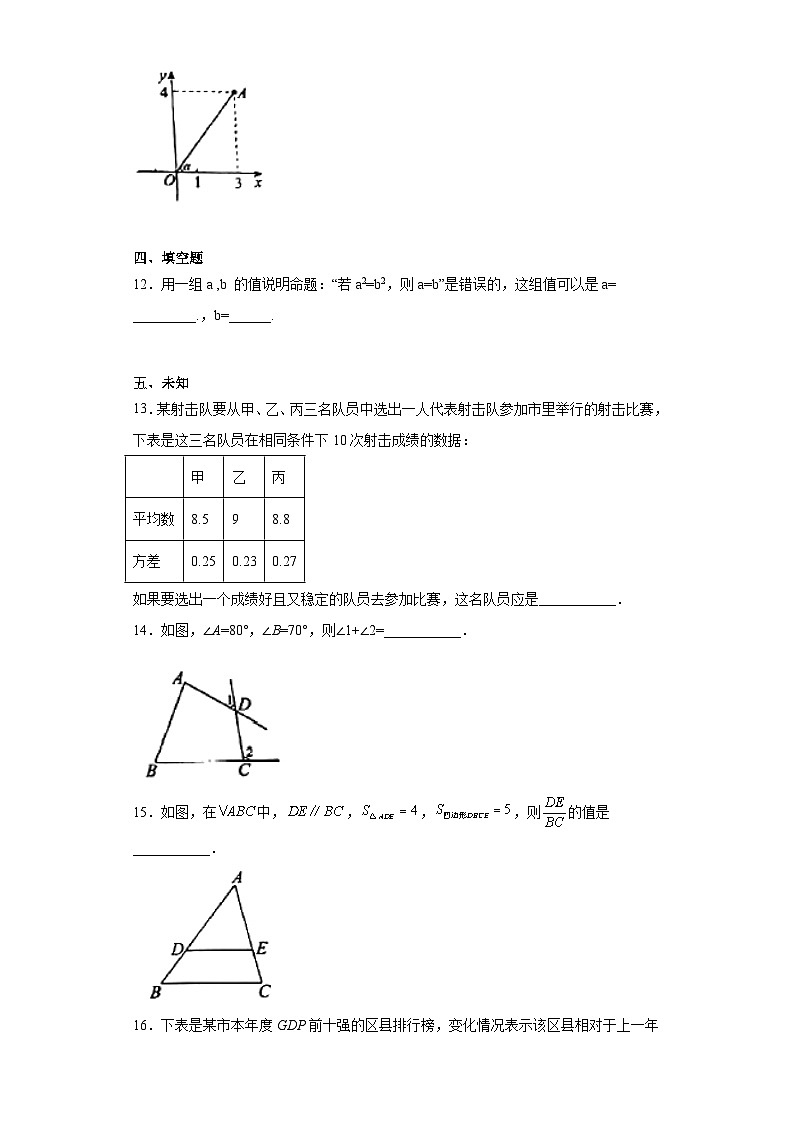
11．如图，在平面直角坐标系xOy中，点A的坐标为（3，4），设线段OA与x轴正方向的夹角为，则___________．

四、填空题

12．用一组a ,b 的值说明命题：“若a2=b2，则a=b”是错误的，这组值可以是a= _________.，b=______.

五、未知

13．某射击队要从甲、乙、丙三名队员中选出一人代表射击队参加市里举行的射击比赛，下表是这三名队员在相同条件下10次射击成绩的数据：

如果要选出一个成绩好且又稳定的队员去参加比赛，这名队员应是___________．

14．如图，∠A=80°，∠B=70°，则∠1+∠2=___________．

15．如图，在中，，，，则的值是___________．

16．下表是某市本年度GDP前十强的区县排行榜，变化情况表示该区县相对于上一年度名次变化的情况，“↑”表示上升，“↓”表示下降，“一”则表示名次没有变化．已知每个区县的名次变化都不超过两位，上一年度排名第1的区县是___________，上一年度排在第6，7，8名的区县依次是___________．（写出一种符合条件的排序）

17．计算：．

18．解不等式组，并写出它的所有正整数解．

19．已知：如图1，线段a，b．

求作：矩形ABCD，使得，．

作法：如图2．

1.在直线上截取．

2.过点B作直线，在直线m上截取．

3.分别以点A和点C为圆心，b，a的长为半径画弧，两弧的交点为D．

（点D与点C在直线的同侧）

4.连接AD，CD．

则四边形ABCD为所求的矩形．

根据上面设计的尺规作图过程，

(1)使用直尺和圆规，在图2中补全图形（保留作图痕迹）；

(2)完成下面的证明：

证明：∵，，

∴四边形ABCD是平行四边形（___________）．（填推理的依据）

∵直线，

∴___________，

∴四边形ABCD是矩形（___________）．（填推理的依据）．

20．已知，求代数式的值．

21．关于x的方程有实数根，且m为正整数，求m的值及此时方程的根．

22．如图，矩形ABCD的对角线AC，BD相交于点O，过点D作AC的平行线交BC的延长线于点E．

(1)求证：；

(2)连接OE，若，，求OE的长．

23．为增强居民的反诈骗意识，A，B两个小区的居委会组织小区居民进行了有关反诈骗知识的有奖问答活动．现从A，B小区参加这次有奖问答活动居民的成绩中各随机抽取20个数据，分别对这20个数据进行整理、描述和分析，下面给出了部分信息．

a．A小区参加有奖问答活动的20名居民成绩的数据的频数分布直方图如下（数据分成5组：，，，，）；

b．A小区参加有奖问答活动的20名居民成绩的数据在这一组的是：

84　　85　　85　　86　　86　　88　　89

c．B小区参加有奖问答活动的20名居民成绩的数据如下：

根据以上信息，解答下列问题：

(1)补全a中频数分布直方图；

(2)A小区参加有奖问答活动的20名居民成绩的数据的中位数是___________；B小区参加有奖问答活动的20名居民成绩的数据的众数是___________；

(3)为鼓励居民继续关注反诈骗宣传，对在这次有奖问答活动中成绩大于或等于90分的居民颁发小奖品．已知A，B两个小区各有2000名居民参加这次活动，估计这两个小区的居委会一共需要准备多少份小奖品．

24．如图，以菱形ABCD的边AD为直径作⊙O交AB于点E，连接DB交⊙O于点M，F是BC上的一点，且，连接DF．

(1)求证：；

(2)求证：DF是⊙O的切线．

25．在平面直角坐标系xOy中，函数的图象与一次函数的图象交于点A（a，2）．

(1)求a，k的值；

(2)横、纵坐标都是整数的点叫做整点．点P是射线OA上一点，过点P分别作x轴，y轴的垂线交函数的图象于点B，C．将线段PB，PC和函数的图象在点B，C之间的部分所围成的区域（不含边界）记为W．

利用函数图象解决下列问题：

①若点P的横坐标是2，直接写出区域W内整点个数；

②若区域W内恰有5个整点，直接写出点P的横坐标的取值范围．

26．在平面直角坐标系xOy中，点，都在抛物线上，且，．

(1)当时，比较，的大小关系，并说明理由；

(2)若存在，，满足，求m的取值范围．

27．如图，在中，边AB绕点B顺时针旋转（）得到线段BD，边AC绕点C逆时针旋转得到线段CE，连接DE，点F是DE的中点．

(1)以点F为对称中心，作点C关于点F的对称点G，连接BG，DG．

①依题意补全图形，并证明；

②求证：；

(2)若，且于H，直接写出用等式表示的FH与BC的数量关系．

28．在平面直角坐标系xOy中，给定圆C和点P，若过点P最多可以作出k条不同的直线，且这些直线被圆C所截得的线段长度为正整数，则称点P关于圆C的特征值为k．已知圆O的半径为2，

(1)若点M的坐标为（1，1），则经过点M的直线被圆O截得的弦长的最小值为___________，点M关于圆O的特征值为___________；

(2)直线分别与x，y轴交于点A，B，若线段AB上总存在关于圆O的特征值为4的点，求b的取值范围；

(3)点T是x轴正半轴上一点，圆T的半径为1，点R，S分别在圆O与圆T上，点R关于圆T的特征值记为r，点S关于圆O的特征值记为s．当点T在x轴正轴上运动时，若存在点R，S，使得，直接写出点T的横坐标t的取值范围．