

湖北省武汉市2023届高三5月模拟训练数学试题(无答案)
展开湖北省武汉市2023届高三5月模拟训练数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设集合,,则( )
A. B.
C. D.
2.设复数满足为纯虚数,则( )
A. B. C. D.
二、未知
3.已知:,:,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知,为单位向量,若,则( )
A. B.
C. D.
5.函数的部分图象可能为( )
A. B.
C. D.
6.将按照某种顺序排成一列得到数列,对任意,如果,那么称数对构成数列的一个逆序对.若,则恰有2个逆序对的数列的个数为( )
A.4 B.5 C.6 D.7
7.已知点M,N是抛物线:和动圆C:的两个公共点,点F是的焦点,当MN是圆C的直径时,直线MN的斜率为2,则当变化时,的最小值为( )
A.3 B.4 C.5 D.6
8.已知,,,则a,b,c的大小关系为( )
A. B.
C. D.
三、多选题
9.已知圆:,直线:,则( )
A.直线在y轴上的截距为1
B.直线的倾斜角为
C.直线与圆有2个交点
D.圆上的点到直线的最大距离为
四、未知
10.在去年的足球联赛上,甲队每场比赛平均失球数是1.5,方差为1.1;乙队每场比赛平均失球数是2.1,方差是0.4,下列说法正确的有( )
A.平均来说甲队比乙队防守技术好
B.乙队比甲队的防守技术更稳定
C.每轮比赛甲队的失球数一定比乙队少
D.乙队可能有一半的场次不失球
11.已知函数,其中,,则( )
A.若存在最小正周期且,则
B.若,则存在最小正周期且
C.若,,则的所有零点之和为2
D.若,,则在上恰有2个极值点
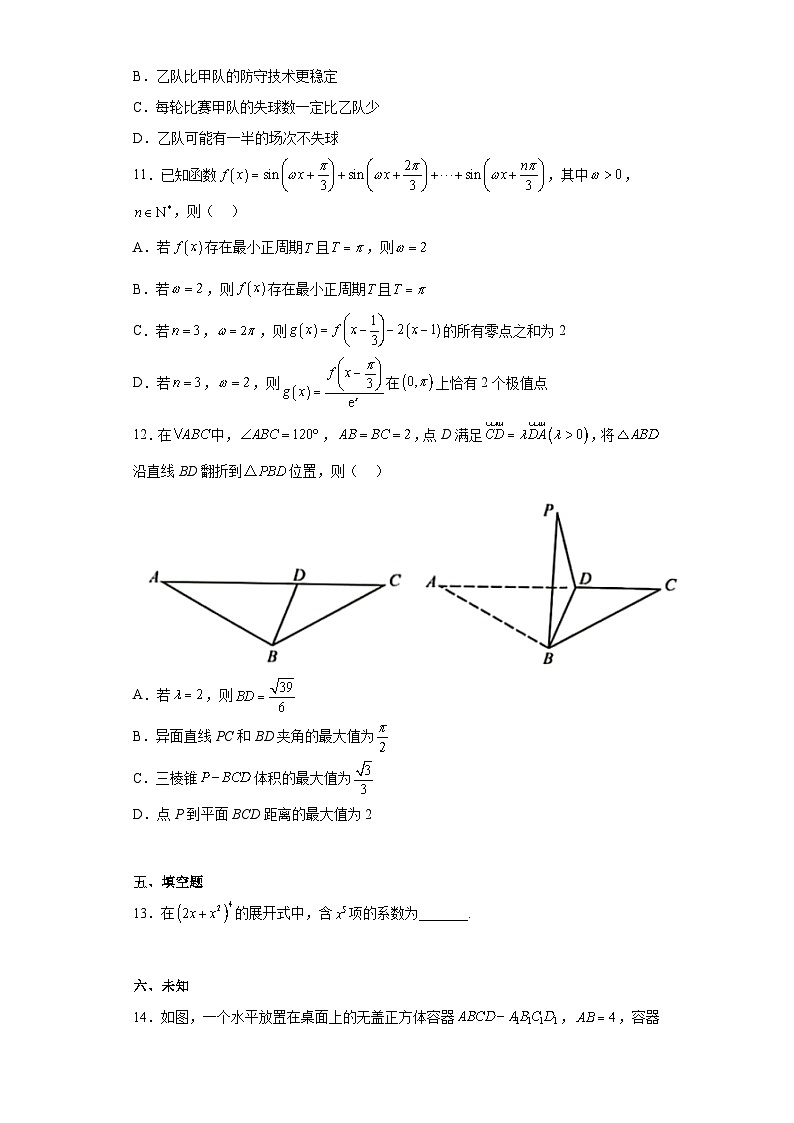
12.在中,,,点D满足,将沿直线BD翻折到位置,则( )
A.若,则
B.异面直线PC和BD夹角的最大值为
C.三棱锥体积的最大值为
D.点Р到平面BCD距离的最大值为2
五、填空题
13.在的展开式中,含项的系数为_______.
六、未知
14.如图,一个水平放置在桌面上的无盖正方体容器,,容器内装有高度为的水,现将容器绕着棱所在直线顺时针旋转45°,容器中溢出的水刚好装满一个半径为的半球形容器,不考虑容器厚度以及其它因素影响,则_______.
七、双空题
15.设样本空间含有等可能的样本点,且,,,则A,B,C三个事件________(填“是”或“不是”)两两独立,且________.
八、未知
16.已知椭圆:,点A,B分别为椭圆C的左右顶点,点F为椭圆C的右焦点,Р为椭圆上一点,且PF垂直于x轴.过原点О作直线PA的垂线,垂足为M,过原点О作直线PB的垂线,垂足为N,记,分别为,的面积.若,则椭圆的离心率为_________.
九、解答题
17.已知各项均不为零的数列的前项和为,,.
(1)求的通项公式;
(2)若恒成立,求正整数的最大值.
十、未知
18.的内角A,B,C的对边分别为a,b,c,且.
(1)求角A;
(2)若,求的面积.
十一、解答题
19.如图,在四棱锥中,底面ABCD为正方形,平面ABCD,,为线段PB的中点,F为线段BC上的动点.
(1)求证:平面平面PBC;
(2)求平面AEF与平面PDC夹角的最小值.
20.2023年5月10日长征七号火箭剑指苍穹,搭载天舟六号货运飞船为中国空间站运送补给物资,为中国空间站的航天员们长时间探索宇宙奥秘提供强有力的后援支持.某校部分学生十分关注中国空间站的发展,若将累计关注中国空间站发展的消息达到6次及以上者称为“航天达人”,未达到6次者称为“非航天达人”.现从该校随机抽取50人进行分析,得到数据如表所示:
| 航天达人 | 非航天达人 | 合计 |
男 | 20 |
| 26 |
女 |
| 14 |
|
合计 |
|
|
|
(1)补全2×2列联表,根据小概率值的独立性检验,能否认为“航天达人”与性别有关联?
(2)现从抽取的“航天达人”中,按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取3人,记这3人中女“航天达人”的人数为X,求X的分布列和数学期望.
附:
0.100 | 0.050 | 0.010 | 0.005 | 0.001 | |
2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
十二、未知
21.新郦已知双曲线:的一条渐近线为,椭圆:的长轴长为4,其中.过点的动直线交于A,B两点,过点Р的动直线交于M,N两点.
(1)求双曲线和椭圆的方程;
(2)是否存在定点Q,使得四条直线QA,QB,QM,QN的斜率之和为定值?若存在,求出点Q坐标;若不存在,说明理由.
十三、解答题
22.已知,其中.
(1)若,讨论的单调性;
(2)已知是的两个零点,且,证明:.
2023届湖北省武汉市高三5月模拟训练数学试题含解析: 这是一份2023届湖北省武汉市高三5月模拟训练数学试题含解析,共22页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。
湖北省武汉市2023届高三5月模拟训练(武汉5调)数学+Word版含答案: 这是一份湖北省武汉市2023届高三5月模拟训练(武汉5调)数学+Word版含答案,共14页。试卷主要包含了已知,为单位向量,若,则,函数的部分图象可能为,已知点M,N是抛物线,已知圆等内容,欢迎下载使用。
湖北省武汉市2023届高三数学5月模拟训练(武汉5调)(Word版附答案): 这是一份湖北省武汉市2023届高三数学5月模拟训练(武汉5调)(Word版附答案),共14页。试卷主要包含了已知,为单位向量,若,则,函数的部分图象可能为,已知点M,N是抛物线,已知圆等内容,欢迎下载使用。












