




- 专题03《三位数乘两位数》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版 试卷 4 次下载
- 专题04《用计算器计算》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版 试卷 3 次下载
- 专题05《解决问题的策略》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版 试卷 4 次下载
- 专题07《三角形、平行四边形和梯形》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版 试卷 5 次下载
- 专题08《确定位置》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版 试卷 4 次下载
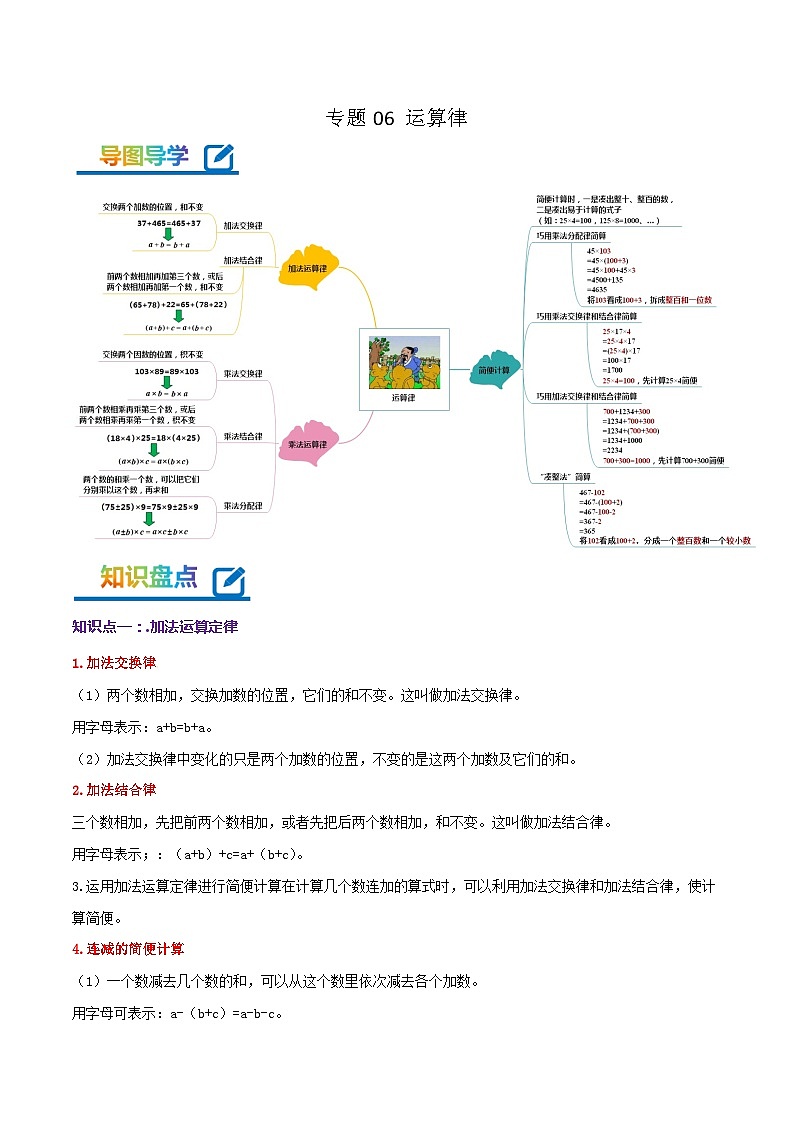
专题06《运算律》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版
展开知识点一:.加法运算定律
1.加法交换律
(1)两个数相加,交换加数的位置,它们的和不变。这叫做加法交换律。
用字母表示:a+b=b+a。
(2)加法交换律中变化的只是两个加数的位置,不变的是这两个加数及它们的和。
2.加法结合律
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫做加法结合律。
用字母表示;:(a+b)+c=a+(b+c)。
3.运用加法运算定律进行简便计算在计算几个数连加的算式时,可以利用加法交换律和加法结合律,使计算简便。
4.连减的简便计算
(1)一个数减去几个数的和,可以从这个数里依次减去各个加数。
用字母可表示:a-(b+c)=a-b-c。
(2)一个数连续减去几个数,可以先把所有的减数加起来,再从被减数里减去所有减数的和。用字母可表示:a -b-c=a-(b+c)。
知识点二:.乘法交换律
1.乘法交换律
两个数相乘,交换两个因数的位置,积不变。这叫做乘法交换律。用字母表示:a×b=b×ag
2.乘法结合律
三个数相乘,先乘前两个数,或者先乘后两个数,积不变。这叫做乘法结合律。用字母表示:(a×b)×c=a×(b×c)。
3.乘法分配律(两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。用字母表示:(a+b)×c=a×c+b×c
知识点三:乘法及连除的简便计算
1.同一道乘法算式的不同简算方法:
计算某些特殊的乘法算式时,可以将其中一个因数折分成两个数的积,再运用乘法交换律和乘法结合律来进行简算;也可以将其中一个因数折分成两个数的和,再运用乘法分配律来进行简算。
2.连除的简便计算
(1)一个数连续除以两个数,可以改为除以两个数的积。
用字母可表示为:a÷b÷c=a÷(b ×c)。(b‡0,c‡0)
(2)一个数除以两个数的积,可以改为连续除以这两个数。
用字母可表示为:a÷(b×c)=a÷b÷c。(b‡0,c‡0)
知识点四:行程问题
A、相遇(或相背)问题(行走方向相反):
方法一:甲速度×相遇时间+乙速度×相遇时间=甲乙两地相距的路程
方法二:(甲速度+乙速度)×相遇时间=甲乙两地相距的路程 即速度之和×时间=路程之和
B、同向而行(行走方向相同)
方法一:甲速度×时间-乙速度×时间=甲乙两车相距的路程
方法二:(甲速度-乙速度)×时间=甲乙两车相距的路程 即速度之差×时间=路程之差
攻略一:加法运算定律及其运用
1、在应用加法运算律进行简便计算时,有时会同时使用加法结合律和加法交换律。
2、加法结合律和加法交换律进行比较:加法结合律改变了运算顺序,加法交换律改变了加数的位置。
3、使用加法结合律进行简便计算时,一定要加上小括号。
攻略二:乘法运算定律及其运用
1、在应用乘法运算律进行简便计算时,有时会同时使用到两种或两种以上的运算律。
2、判断是否运用了乘法交换律,不仅看结果是否相同,还要看乘数有没有交换位置,以及乘数是否变化。
3、乘法交换律和乘法结合律的比较:乘法交换律改变了乘数的位置,乘法结合律改变了运算顺序。
4、利用分配律计算时,乘数需与两个加数分别相乘。
5、应用乘法分配律进行简便计算时,要注意拆分形式为(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c。
一.精挑细选(共5小题,满分10分,每小题2分)
1.(2分)(2023春•汉川市期中)小明在运用乘法分配律简便计算103×15时,错算成103×15=100×15+3,这样的计算结果比正确结果少( )
A.45B.42C.15
【易错点拨】计算103×15时,将103化成(100+3),再利用乘法分配律计算;计算100×15+3时,先算乘法,再算加法;最后求出两个算式的差即可。
【规范解答】解:103×15
=(100+3)×15
=100×15+3×15
=1500+45
=1545
100×15+3
=1500+3
=1503
1545﹣1503=42
答:这样的计算结果比正确结果少42。
故选:B。
【题后反思】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律。
2.(2分)(2023春•海丰县期中)下面算式错误的是( )
A.38×109=38×100+9×38
B.7×98=7×100﹣2
C.2700÷25÷4=2700÷100
D.185﹣58﹣42=185﹣(58+42)
【易错点拨】根据乘法分配律、除法的性质以及减法的性质对各个选项进行分析,找出计算错误的选项即可。
【规范解答】解:选项A:38×109
=38×(100+9)
=38×100+9×38
=3800+342
=4142
本选项计算正确;
选项B:7×98
=7×(100﹣2)
=7×100﹣7×2
=700﹣14
=686
本选项计算错误;
选项C:2700÷25÷4
2700÷(25×4)
=2700÷100
=27
本选项计算正确;
选项D:185﹣58﹣42
=185﹣(58+42)
=186﹣100
=85
本选项计算正确。
故选:B。
【题后反思】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
3.(2分)(2023春•乌鲁木齐期中)(x+y)+z=x+(y+z),这道算式运用( )
A.加法结合律B.加法交换律C.乘法交换律
【易错点拨】先把前两个数相加,或者把后两个数相加,和不变,这叫做加法结合律.
【规范解答】解:(x+y)+z=x+(y+z),这道算式运用了加法结合律;
故选:A.
【题后反思】本题考查了学生对加法结合律的理解与应用.
4.(2分)(2022秋•莱山区期末)在计算1.2×1.25时,强强的方法是“1.2×1.25=1×1+0.2×0.25”这样计算出的结果与正确结果不一致。请结合图分析,强强出错是因为没有计算图中的( )
A.②B.③C.②和③D.②和④
【易错点拨】观察图可知,强强的方法是把计算1.2×1.25转化成了长1.25、宽1.2的长方形的面积,又把这个长方形面积转化成正方形和长方形的面积,找清楚1×1和0.2×0.25是哪两部分的面积,还剩下哪两部分没有算到里面,就是强强漏的部分。
【规范解答】解:
由图可知:
1.2×1.25是大长方形的面积;
1×1是①号正方形的面积;
0.2×0.25是④号长方形的面积;
1.2×1.25=1×1+0.2×0.25缺少了②号长方形和③号长方形的面积。
故选:C。
【题后反思】本题考查了数形结合的思想,把乘法算式转变成了长方形、正方形的面积,找清楚每部分图形的长和宽,从而求解。
5.(2分)在计算125×88时,下面各式中错误的是( )
A.(8×125)×11B.125×(80+8)
C.(125×8)×(11×8)D.125×(90﹣2)
【易错点拨】把88写成8×11,再根据乘法结合律进行计算,或写成80+8,再根据乘法分配律进行计算,或者写成90﹣2,但不能写成8×11×8.
【规范解答】解:125×88
=125×8×11
=1000×11
=11000
125×88
=125×(80+8)
=125×80+125×8
=10000+1000
=11000
(125×8)×(11×8)
=1000×88
=88000
125×88
=125×(90﹣2)
故选:C.
【题后反思】完成本题要注意分析式中数据,运用合适的简便方法计算.
二.仔细想,认真填(共8小题,满分18分)
6.(2分)(2023春•汉川市期中)如果35×A+35×B运用乘法分配律进行简便计算后,结果是3500,则A可以是 40 ,B可以是 60 。(只写一种)
【易错点拨】先将35×A+35×B运用乘法分配律化成35(A+B),再根据因数与积之间的关系,用3500除以35,求出A加B的和,然后根据加数与和的关系写出一组A和B的值即可。
【规范解答】解:35×A+35×B=35(A+B)
A+B=3500÷35=100
100=40+60
答:A可以是40,B可以是60。
故答案为:40,60。(答案不唯一)
【题后反思】解答本题需熟练掌握乘法分配律、因数与积之间的关系及加数与和之间的关系。
7.(2分)(2023春•项城市期中)28×25÷28×25= 625 ,如果△+□=30,那么12×△+12×□= 360 。
【易错点拨】(1)计算28×25÷28×25,先算28÷28,再算1×25×25;
(2)根据乘法分配律,12×△+12×□=12×(△+□),再将△+□=30代入算式12×(△+□)计算即可。
【规范解答】解:(1)28×25÷28×25
=28÷28×25×25
=1×25×25
=625
(2)12×△+12×□
=12×(△+□)
当△+□=30时,12×(△+□)=12×30=360。
故答案为:625;360。
【题后反思】解答本题需灵活利用运算律和运算性质,熟练利用代入法求值。
8.(2分)(2023春•南宫市月考)算式14+156+286+244=(14+286)+(156+244)既运用了加法 交换 律,又运用了加法 结合 律。
【易错点拨】利用加法交换律和加法结合律计算后填空即可。
【规范解答】解:14+156+286+244
=(14+286)+(156+244)
=300+400
=700
计算过程既运用了加法交换律,又运用了加法结合律。
故答案为:交换、结合。
【题后反思】解答本题需熟练掌握加法交换律和加法结合律公式。
9.(2分)(2022秋•禹城市期末)4×2.5请按小巧和小茸的算法继续往下算,并完成填空:
【易错点拨】小巧计算时,应用了乘法交换律、乘法结合律;小茸计算时,应用了乘法分配律.
【规范解答】解:
故答案为:4×2.5×1.1
=10×1.1
=11
乘法交换律、乘法结合;
4×2.5+0.4×2.5
=10+1
=11
乘法分配。
【题后反思】此题主要考查了小数乘小数的运算方法,要熟练掌握,注意乘法运算定律的应用.
10.(2分)(2022春•红安县期末)B×228﹣B×28=B× (228﹣28) ,这是根据 乘法分配律 进行简便计算的。
【易错点拨】乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加;据此可知,B×228﹣B×28=B×200,这是根据乘法分配律进行简便计算的。
【规范解答】解:B×228﹣B×28
=B×(228﹣28)
=B×200
=200B
所以B×228﹣B×28=B×200,这是根据乘法分配律进行简便计算的。
故答案为:(228﹣28),乘法分配律。
【题后反思】正确理解乘法分配律的意义,是解答此题的关键。
11.(4分)(2022春•固始县期中)在横线里填上“>”、“<”或“=”。
【易错点拨】(1)先根据乘法分配律把99×35变形,再比较:99×35=(100﹣1)×35=100×35﹣35;
(2)先根据除法的性质把96÷8÷2变形后再比较:96÷8÷2=96÷(8×2),8×2>8÷2,被除数相同都是96,除数越大,商越小,所以96÷(8×2)<96÷(8÷2);
(3)根据加法结合律可知:428+(500﹣128)=428+500﹣128;
(4)先根据乘法分配律把左边算式变形后,再比较;60×25+28×25=(60+28)×25,60+28>60﹣28,一个乘数相同是25,另一个乘数越大积越大,所以 (60+28)×25>(60﹣28)×25。
【规范解答】解:
故答案为:=,<,=,>。
【题后反思】解决本题注意观察算式的特点,根据算式的不同选择合适的方法进行比较。
12.(2分)(2021春•闽侯县月考)小虎在计算675÷15时,错误地写成了675÷45,将小虎的计算结果 乘3 就能得到正确的答案。
【易错点拨】算式675÷15错误地写成了675÷45,被除数没变,除数乘了3,商就要除以3,所以要想得到原来算式正确的商需要再乘3,据此即可解答。
【规范解答】解:小虎在计算675÷15时,错误地写成了675÷45,将小虎的计算结果乘3就能得到正确的答案。
故答案为:乘3。
【题后反思】本题考查了商的变化规律,被除数不变,除数乘(除以)几(0除外),商要除以(乘)几。
13.(2分)(71﹣36)×20=71×20﹣36×20是应用了 乘法分配 律.
【易错点拨】根据乘法分配律的意义,(a﹣b)×c=a×c﹣b×c,据此解答.
【规范解答】解:(71﹣36)×20
=71×20﹣36×20
=1420﹣720
=700.
故答案为:乘法分配律.
【题后反思】此题考查的目的是理解掌握乘法分配律的意义及应用.
三.判断正误(共5小题,满分5分,每小题1分)
14.(1分)(2023春•嘉祥县期中)65+130+35+70=(65+35)+(130+70),只运用了加法交换律。 × (判断对错)
【易错点拨】根据加法交换律、加法结合律的意义,先运用加法交换律,再运用加法结合律简算。
【规范解答】解:65+130+35+70
=(65+35)+(130+70)
=100+200
=300
所以运用了加法交换律和加法结合律。
因此,题干中的结论是错误的。
故答案为:×。
【题后反思】此题考查的目的是理解掌握加法交换律、加法结合律的意义,并且能够灵活运用加法交换律、加法结合律进行简算。
15.(1分)(2023春•黄石期中)840÷2÷4与840÷(2×4)的结果相同. √ (判断对错)
【易错点拨】840÷2÷4按照从左到右的顺序计算出算式的结果,840÷(2×4)先算小括号里面的乘法,再算括号外的除法计算出算式的结果,再比较即可判断.
【规范解答】解:840÷2÷4
=420÷4
=105
840÷(2×4)
=840÷8
=105
105=105,原题说法正确.
故答案为:√.
【题后反思】本题也可以直接根据除法的性质进行判断:连续除以两个数等于除以这两个数的积.
16.(1分)(2022秋•贵州期中)0.25×9.9=0.25×(10﹣0.1)=0.25×10﹣0.25×0.1=2.5﹣0.025=2.475。 √ (判断对错)
【易错点拨】0.25×9.9,转化为:0.25×(10﹣0.1),再运用乘法分配律进行简算,然后再判断。
【规范解答】解:0.25×9.9
=0.25×(10﹣0.1)
=0.25×10﹣0.25×0.1
=2.5﹣0.025
=2.475
因此题干中的结论是正确的。
故答案为:√。
【题后反思】此题考查的目的是理解掌握乘法分配律的意义及应用。
17.(1分)(2021秋•曲江区期末)89×102=89×100+2。 × (判断对错)
【易错点拨】根据乘法分配律的意义,(a+b)×c=a×c+b×c,据此判断。
【规范解答】解:89×102
=89×(100+2)
=89×100+89×2
=8900+178
=9078
因此,题干中的结论是错误的。
故答案为:×。
【题后反思】此题考查的目的是理解掌握乘法分配律的意义及应用。
18.(1分)(2021春•霸州市期末)125×4×25×8=(125×8)+(25×4). × (判断对错)
【易错点拨】125×4×25×8运用乘法交换律和结合律,即4和8交换,然后125和8结合,25和4结合,应该等于(125×8)×(25×4),据此判断.
【规范解答】解:125×4×25×8
=(125×8)×(25×4)
=1000×100
=100000;
这是运用了乘法交换律和结合律;
所以题干说法错误.
故答案为:×.
【题后反思】此题考查学生对乘法分配律与乘法交换律和结合律的理解和掌握情况,不能混为一谈.
四.计算能手(共1小题,满分12分,每小题12分)
19.(12分)(2023春•苍南县期中)计算下面各题,能简便地用简便方法计算。
【易错点拨】(1)先算小括号里的减法,再算中括号里的除法,最后再算除法即可;
(2)利用除法的性质计算;
(3)根据加法交换律和结合律进行简算即可;
(4)利用减法的性质计算;
(5)把32分成8×4,再根据乘法结合律进行简算即可;
(6)利用乘分配律的逆运算进行简算即可。
【规范解答】解:(1)240÷[(240﹣60)÷6]
=240÷[180÷6]
=240÷30
=8
(2)1050÷15÷7
=1050÷(15×7)
=1050÷105
=10
(3)382+29+18+71
=382+18+(29+71)
=400+100
=500
(4)2158﹣(75+158)
=2158﹣158﹣75
=2000﹣75
=1925
(5)32×25
=8×4×25
=8×(4×25)
=8×100
=800
(6)49×63+37×49
=(63+37)×49
=100×49
=4900
【题后反思】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
五.实际应用(共5小题,满分25分,每小题5分)
20.(5分)(2021春•济源期末)公园里有柳树和玉兰树各13行,柳树每行种32棵,玉兰树每行种28棵,两种树共多少棵?
【易错点拨】用柳树每行种的棵数加上玉兰树每行种的棵数,求出每行种柳树和玉兰树一共有多少棵,再乘13,即可求出两种数一共种多少棵。
【规范解答】解:(32+28)×13
=60×13
=780(棵)
答:两种树共780棵。
【题后反思】本题主要考查了两位数乘两位数乘法的灵活应用,也可以用柳树每行种的棵数乘行数,求出柳树一共种多少棵,同理,求出玉兰树每行种多少棵,把它们相加即可,列式为:32×13+28×13。
21.(5分)(2022•南京模拟)超市的一种大米每袋46元,一种面粉每袋54元。学校食堂打算买这样的大米和面粉各55袋,需要多少元钱?
【易错点拨】根据题意:用每袋大米的价钱加上每袋面粉的价钱,求出大米和面积各一袋的价钱。再乘55,求出大米和面粉各55袋的总钱数。
【规范解答】解:(46+54)×55
=100×55
=5500(元)
答:需要5500元钱。
【题后反思】本题考查经济问题,关键是根据总价=单价×数量解答。
22.(5分)四季超市运来大米和面粉各48袋,大米每袋75千克,面粉每袋25千克,一共运来大米和面粉共多少千克?
【易错点拨】根据题意可知,大米的袋数×每袋大米的重量+面粉的袋数×每袋大米的重量=一共运来大米和面粉的总重量,依此列式并根据乘法分配律的特点进行计算即可。
【规范解答】解:48×75+48×25
=48×(75+25)
=48×100
=4800(千克)
答:一共运来大米和面粉共4800千克。
【题后反思】此题考查的是运用乘法分配律的特点解决实际问题,应熟练掌握。
23.(5分)小军和小英同时从学校出发,沿同一条路到少年宫,小军每分钟行70米,小英每分钟行60米.10分钟后小军到了少年宫,这时小英离少年宫还有多少米?(先画图,再解答)
【易错点拨】先依据路程=速度×时间,分别求出小军和小英行驶的路程,再用小军行驶的路程减小英行驶的路程即可解答.
【规范解答】解:
70×10﹣60×10
=700﹣600
=100(米)
答:这时小英离少年宫还有100米.
【题后反思】注意两人是朝同一个方向行驶,关键是求出两人行驶的路程.
24.(5分)(2022秋•房山区期末)小明计算74×19+26×19,他是这样计算的:74×19+26×19=(74+26)×19。
(1)小明用的是哪个运算律?请你用自己喜欢的方式表示出这个运算律。
(2)芳芳根据上面题目中用到的运算律计算图形的面积,请你把解决问题的过程补充完整。(图中单位:厘米)
18×14+12×14
= (18+12)×14
= 30×14
= 420 (平方厘米)
(3)请你根据上面的运算律讲一个生活中的数学故事。(可以写一写、画一画)
【易错点拨】(1)74×19+26×19=(74+26)×19,这是逆用了乘法分配律,可以用字母为:a×c+b×c=(a+b)×c;
(2)图中两个小长方形的面积可以分别表示为:18×14平方厘米和12×14平方厘米,它们的和就是大长方形的面积;大长方形的长是(18+12)厘米,宽是14厘米,所以大长方形的面积就是(18+12)×14平方厘米,则18×14+12×14=(18+12)×14,符合上面的运算定律;
(3)可以举例说明一下乘法分配律的实际运用。
【规范解答】解:(1)这是运用了乘法分配律,用字母为:a×c+b×c=(a+b)×c;
(2)18×14+12×14
=(18+12)×14
=30×14
=420(平方厘米)
(3)商店运来一些苹果和梨各25筐,苹果每筐15千克,梨每筐25千克,求运来苹果和梨一共多少千克时,可以运用乘法分配律进行解决问题,即:
15×25+25×25
=(15+25)×25
=40×25
=1000(千克)
(答案不唯一)
故答案为:(18+12)×14,30×14,420。
【题后反思】乘法分配律是最常用的简便运算的方法,要熟练掌握,灵活运用。
六.解决问题(共6小题,满分30分)
25.(6分)(2023春•永善县校级月考)东东在学习运算律时,他借助了点子图来计算12×15的过程,计算如下,这道题还可以怎么算呢?请你在右面的点子图上先画一画,再写出计算过程。
【易错点拨】计算12×15时,可以将12化成(10+2),再利用乘法分配律计算。
【规范解答】解:
12×15
=(10+2)×15
=10×15+2×15
=150+30
=180
【题后反思】本题考查了乘法分配律在两位数乘两位数中的应用,结合点子图,突出了对算理的理解。
26.(6分)(2021春•新都区期末)
(1)你认为他说的“一样”,是指什么一样?
(2)小男孩的说法正确吗?符合什么运算律?
【易错点拨】观察三个算式,找出共同点,然后判断符合哪种运算律。
【规范解答】解:(1)他说的“一样”,是指列竖式计算时数位对齐。
(2)男孩的说法正确,符合乘法分配律。
【题后反思】本题考查了列竖式计算,其算理符合乘法分配律。
27.(3分)(2018秋•南康区期末)计算下面三组题.
通过计算后我发现: 一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数. .
【易错点拨】除法基本性质:一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数. a÷b÷c=a÷(b×c)=a÷c÷b
【规范解答】解:①160÷(4×8)
=160÷32
=5
160÷4÷8
=40÷8
=5
②96÷(3×8)
=96÷24
=4
96÷3÷8
=32÷8
=4
③105÷(5×7)
=105÷35
=5
105÷5÷7
=21÷7
=3
故答案为:一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数.
【题后反思】除法基本性质:一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数. a÷b÷c=a÷(b×c)=a÷c÷b
28.(6分)(2022春•忻府区校级期中)戴口罩不仅可以预防过敏或避免吸入大量有害物质,还可以预防呼吸道传染性疾病的发生。“新冠”属于呼吸道传染病的一种。小明的爸爸为了更好地守护家人健康,准备了200元钱去药店购买口罩,其中购买成人口罩10包一共花了60元,购买儿童口罩10包一共花了80元,请你根据以上信息,结合第四单元学习的探索运算规律的一般方法,试着研究(a+b)÷c=a÷c+b÷c。
【易错点拨】根据题目中给出的条件,求一包成人口罩和一包儿童口罩一共多少钱,列出两种不同的算式,即可探究运算规律。
【规范解答】解:(1)先求一共花了多少钱,再求一包成人口罩和一包儿童口罩一共多少钱。
(60+80)÷10=14(元)
(2)先求一包成人口罩和一包儿童口罩各多少钱,再求一包成人口罩和一包儿童口罩一共多少钱。
60÷10+80÷10=14(元)
14=14
所以(60+80)÷10=60÷10+80÷10
所以(a+b)÷c=a÷c+b÷c。
【题后反思】本题考查除法的计算方法和乘法分配律的联系。
29.(5分)(2023春•宿迁期中)学校要购买85套桌椅,每张桌子68元,每把椅子32元,78500元够吗?
【易错点拨】先求出一套桌椅的价钱,即68+32=100元,再根据总价=单价×数量,求出总价再与78500元比较即可.
【规范解答】解:(68+32)×85
=100×85
=8500(元),
8500元<78500元;
答:78500元够.
【题后反思】此题关键是先求出85套桌椅的总钱数,再进行大小比较即可.
30.(4分)(2013春•东莞市校级期中)数学门诊部.(对的画“√”,错的画“”,并改正)
【易错点拨】(1)去掉小括号时,应减去43,所以错误;
(2)运用乘法的分配律简算时,应1×47所以错误;
【规范解答】解:
【题后反思】此题考查的目的是理解掌握乘法运算定律的运用小巧算法:4.4×2.5
=4×1.1×2.5=
我运用了 乘法交换律、乘法结合 律使计算简便
小亚法:4.4×2.5
=(4+0.4)×2.5=
我运用了 乘法分配 律使计算简便
小巧算法:
4.4×2.5
=4×1.1×2.5
=4×2.5×1.1
=10×1.1
=11
我运用了乘法交换律、乘法结合律使计算简便
小亚法:
4.4×2.5
=(4+0.4)×2.5
=4×2.5+0.4×2.5
=10+1
=11
我运用了乘法分配律使计算简便
99×35 = 100×35﹣35
96÷8÷2 < 96÷(8÷2)
428+(500﹣128) = 428+500﹣128
60×25+28×25 > (60﹣28)×25
99×35=100×35﹣35
96÷8÷2<96÷(8÷2)
428+(500﹣128)=428+500﹣128
60×25+28×25>(60﹣28)×25
240÷[(240﹣60)÷6]
1050÷15÷7
382+29+18+71
2158﹣(75+158)
32×25
49×63+37×49
160÷(4×8)
96÷(3×8)
105÷(5×7)
160÷4÷8
96÷3÷8
105÷5÷7
专题08《确定位置》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版: 这是一份专题08《确定位置》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版,文件包含专题08确定位置教师版docx、专题08确定位置学生版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
专题05《解决问题的策略》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版: 这是一份专题05《解决问题的策略》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版,文件包含专题05解决问题的策略教师版docx、专题05解决问题的策略学生版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
专题04《用计算器计算》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版: 这是一份专题04《用计算器计算》-2022-2023学年四年级数学下册期末专项复习(学生版+教师版)苏教版,文件包含专题04用计算器计算教师版docx、专题04用计算器计算学生版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。













