2023年山东省青岛市崂山区中考数学二模试卷（含解析）

2023年山东省青岛市崂山区中考数学二模试卷

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.  有理数的倒数为(    )

A.  B.  C.  D.

2.  下列个图形中，是中心对称图形但不是轴对称的图形是(    )

A.  B.  C.  D.

3.  纳米科技是新兴科技，纳米米，则纳米用科学记数法表示为(    )

A. 米 B. 米 C. 米 D. 米

4.  如图，放置于桌面上的几何体，其俯视图为(    )

A.
B.
C.
D.

5.  某小组长统计组内人一天在课堂上的发言次数分别为，，，，关于这组数据，下列说法错误的是(    )

A. 众数是 B. 中位数是 C. 平均数是 D. 极差是

6.  今日，上海疫情防控形势严峻，某工厂计划生产套防护服，由于工人加班加点，实际每天比计划多制作，结果比原计划提前天完成任务．设原计划每天制作套防护服，则可列方程为(    )

A.  B.
C.  D.

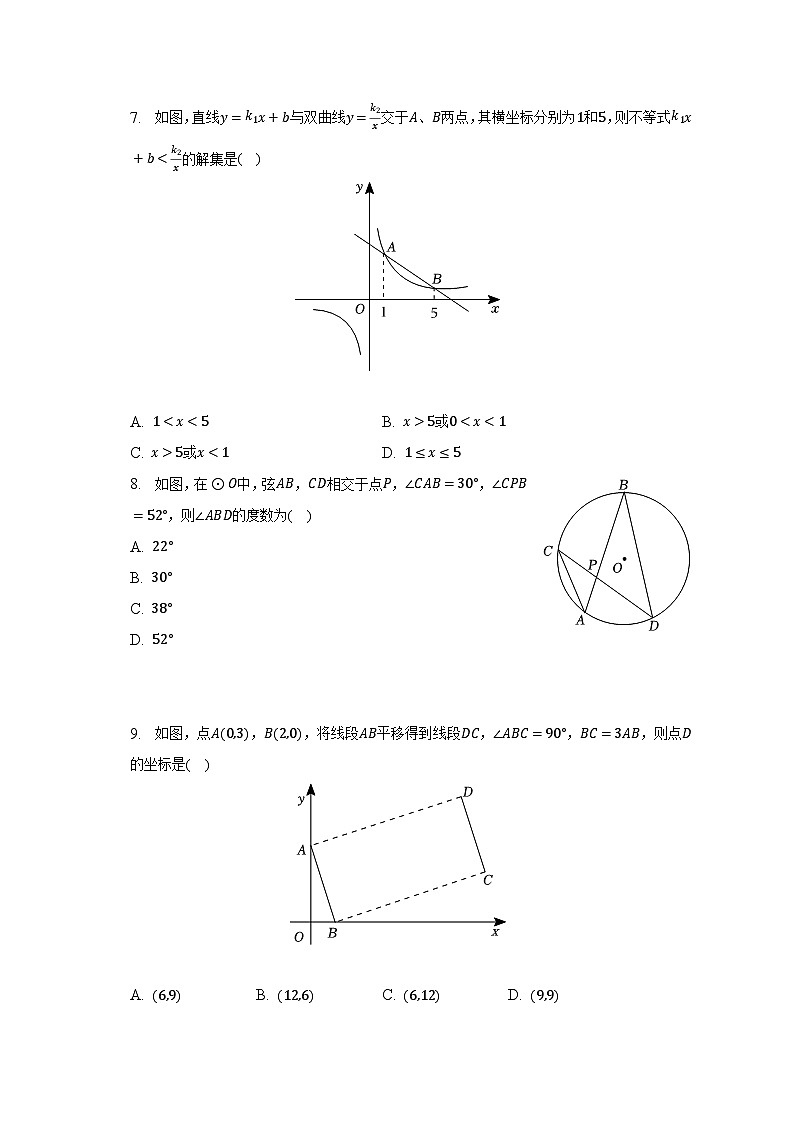
7.  如图，直线与双曲线交于、两点，其横坐标分别为和，则不等式的解集是(    )

A.  B. 或
C. 或 D.

8.  如图，在中，弦，相交于点，，，则的度数为(    )

A.
B.
C.
D.

9.  如图，点，，将线段平移得到线段，，，则点的坐标是(    )

A.  B.  C.  D.

10.  如图，函数的图象的顶点为，下列判断正确个数为(    )
；
；
；
点和点都在此函数图象上，则；
．

A. 个 B. 个 C. 个 D. 个

二、填空题（本大题共6小题，共18.0分）

11.  计算： ______ ．

12.  关于的方程是一元二次方程，则的值为______ ．

13.  如图是一个可以自由转动的转盘，转动转盘，转盘停止后，指针落在区域的概率是______ ．

14.  如图，圆内接正六边形，以顶点为圆心，以长为半径画，若，则的长为______ 结果保留

15.  如图，在矩形纸片中，，，将沿折叠到位置，交于点，则的值为______ ．

16.  如图，在中，，，点是上一点，连接，若，，则 ______ ．

三、解答题（本大题共10小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17.  本小题分
已知：线段，．
求作：，，斜边．

18.  本小题分
计算：
化简；
解不等式组：．

19.  本小题分
共享概念已经进入人们的生活，某同学收集了自己感兴趣的个共享领域的图标，共享出行、共享服务、共享物品、共享知识，制成编号为，，，四张卡片除字母和内容外，其余完全相同现将这四张卡片背面朝上，洗匀放好从中随机抽取两张卡片，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率．
 

20.  本小题分
教育部等五部门关于全面加强和改进新时代学校卫生与健康教育工作的意见要求：保障学生每天校内、校外各个小时体育活动时间，某学校分别随机调查了男、女学生各名，统计他们上周平均每天校外体育锻炼的时间，锻炼时间记为分钟，将所得数据分为个组别组：；组：；组：；组：；组：，将数据进行分析，得到如下统计：
名男生组学生上周平均每天校外体育锻炼时间从高到低排列，排在最后的个数据分别是：，，，，，，，，，；
名男生上周平均每天校外体育锻炼时间条形统计图如图；
名女生上周平均每天校外体育锻炼时间分布扇形统计图如图；
调查的男、女同学上周平均每天校外体育锻炼时间的平均数、中位数、众数如表．

请你根据以上信息，回答下列问题：
根据以上信息填空： ______ ， ______ ，并补全条形统计图；
根据以上数据分析，你认为男生和女生上周校外锻炼情况那个更好，请说明理由；写出一条理由即可
该校有男同学名，女同学名，请估计该校上周平均每天校外体育锻炼时间在分钟以上含分钟的学生一共有多少人．

21.  本小题分
【问题提出】如图，为内接三角形，已知，圆的半径为，探究，，之间的关系．
【解决问题】如图，若为锐角，连接并延长交于点，连接，则，在中，为直径，，所以，．
所以在中建立，，的关系为______ ．
所以在内接三角形中，，，之间的关系为______ ．
类比锐角求法，当为直角和钝角时都有此结论．
【结论应用】
已知三角形中，，，则外接圆的面积为______ ．
 

22.  本小题分
如图，停车场有一处停车位，左侧靠近一面墙，王老师将车停下后，打开车门后，发现车门只能到达处，从车上下不来，于是他将车重新调整，沿与墙面垂直方向向右移动了线段的长度，打开车门后，车门到达处，此时能够顺利下车，已知，，，求车向右移动的距离

23.  本小题分
如图，▱的对角线与相交于点，过点作，过点作，与相交于点．
证明四边形为平行四边形；
给▱添加一个条件，使得四边形为菱形，并说明理由．

24.  本小题分
如图，一次函数与反比例函数的图象在第一象限相交于，两点，点坐标是，垂直轴交轴于点，为坐标原点，，连接．
求反比例函数的关系式；
若点在轴上，的面积和的面积相等，求点的坐标．

25.  本小题分
跳台滑雪简称“跳雪”，选手不借助任何外力、从起滑台处起滑，在助滑道上加速，从跳台处起跳，最后落在山坡或者水平地面上运动员从点起滑，沿滑道加速，到达高度的点后起跳，运动员在空中的运动轨迹是一条抛物线建立如图所示平面直角坐标系，，，设所在直线关系式为．
甲运动员起跳后，与跳台水平距离、竖直高度之间的几组对应数据如下：

求甲运动员空中运动轨迹抛物线的关系式；
运动员得分由距离得分动作分风速得分组成距离得分：运动员着陆点到跳台水平距离为，即得到分，每比远米多得分；反之，当运动员着陆点每比近米扣分距离分计算采取“舍入法”，如米计为米，米则计为米．
动作得分：由裁判根据运动员空中动作的优美程度打分．
风速得分：由逆风或者顺风决定．
甲运动员动作分、风速加分如下表：

请你计算甲运动员本次比赛得分．

26.  本小题分
已知：如图，在四边形中，，，，连接，点从点出发，沿方向匀速运动，速度为；同时，点从点出发，沿方向匀速运动，速度为，连接，设运动时间为．
当为何值时，点在线段的垂直平分线上？
延长交于点如图，若四边形是平行四边形求的值；
设的面积为，求与的函数关系式，并求的最大值；
是否存在某一时刻，使得与的夹角为？若存在，请求出此时的值；若不存在，请说明理由．

答案和解析

1.【答案】 

【解析】解：，
的倒数为，
的相反数为，
故选：．
先将化简，再根据相反数的定义即可求解．
本题主要考查了倒数，掌握倒数的定义是解题的关键．
 

2.【答案】 

【解析】解：、不是轴对称图形，也不是中心对称图形，故此选项错误；
B、是轴对称图形，也是中心对称图形，故此选项错误；
C、是轴对称图形，不是中心对称图形，故此选项错误；
D、不是轴对称图形，是中心对称图形，符合题意．
故选：．
根据轴对称图形与中心对称图形的概念求解．
此题主要考查了轴对称图形和中心对称图形，掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转度后与原图重合．
 

3.【答案】 

【解析】解：纳米米米．
故选：．
绝对值小于的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的的个数所决定．
 

4.【答案】 

【解析】解：如图，它的俯视图为：

故选：．
根据从上边看得到的图形是俯视图，可得答案．
本题考查了三视图的知识，掌握“俯视图是从物体的上面看到的视图”是解本题的关键．
 

5.【答案】 

【解析】解：将数据重新排列为，，，，，
则这组数的众数为，中位数为，平均数为，极差为，
故选：．
根据方差、众数、平均数、中位数的含义和求法，逐一判断即可．
本题考查了众数、中位数、平均数以及极差，解题的关键是牢记概念及公式．
 

6.【答案】 

【解析】解：设原计划每天制作套防护服，
可列方程为：，
故选：．
设原计划每天制作套防护服，则实际每天制作为，根据结果比原计划提前天完成任务，列出方程即可．
本题考查了由实际问题抽象出分式方程，关键是读懂题意，设出未知数，找出合适的等量关系，列出方程．
 

7.【答案】 

【解析】解：根据图象，可得：不等式的解集为一次函数图象在反比例函数图象下方时的取值范围，
又直线与双曲线交于、两点，其横坐标分别为和，
不等式的解集是：
或．
故选：．
根据题意，得出不等式的解集为一次函数图象在反比例函数图象下方时的取值范围，然后再根据图象，即可得出答案．
本题考查了一次函数与反比例函数的交点问题、求不等式的解集，解本题的关键在充分利用数形结合思想解答．
 

8.【答案】 

【解析】解：，
，
在中，，
．
故选：．
根据圆周角定理可知，然后根据三角形外角的性质可进行求解．
本题主要考查圆周角定理，熟练掌握同弧所对圆周角相等是解题的关键．
 

9.【答案】 

【解析】解：过点作轴于点，如图，

点、，
，，
线段平移得到线段，
，，
四边形是平行四边形，
，
四边形是矩形，
，，
，
，
，，
，
，
∽，
，
，，
，
．
故选：．
过点作轴于点，利用点，的坐标表示出线段，的长，利用平移的性质和矩形的判定定理得到四边形是矩形；利用相似三角形的判定与性质求得线段，的长，进而得到的长，则结论可得．
本题主要考查了图形的变化与坐标的关系，平移的性质，矩形的判定与性质，相似三角形的判定与性质，利用点的坐标表示出相应线段的长度是解题的关键．
 

10.【答案】 

【解析】解：抛物线开口向下，
，
函数的图象的顶点为，
抛物线的对称轴为直线，
，
，故错误；
由上述可知，，
，故正确；
抛物线开口向下，
当时，取得最大值为，
无论取何值都有，
，故错误；
抛物线的对称轴为直线，，
，故正确；
函数的图象的顶点为，
，
整理得：，
，
，
，故正确．
综上，正确的结论有，共个．
故选：．
根据抛物线的开口方向得，由顶点坐标可得，，以此可判断；再根据二次函数的性质可得当时，取得最大值为，以此可判断；根据离抛物线对称轴距离相等点的函数值相等可判断；将顶点坐标代入函数解析式中，化简即可判断．
本题主要考查二次函数图象与系数之间的关系、二次函数的图象与性质，解题关键在于熟练掌握二次函数的性质，利用数形结合思想答题．
 

11.【答案】 

【解析】解：原式

故答案为：
先利用幂的乘方与积的乘方的法则运算，再利用单项式除以单项式的法则运算即可．
本题主要考查了整式的除法，幂的乘方与积的乘方，熟练掌握上述法则与性质是解题的关键．
 

12.【答案】 

【解析】解：关于的方程是一元二次方程，
，
解得：，
的值为．
故答案为：．
利用一元二次方程的定义，可得出，解之即可求出的值．
本题考查了一元二次方程的定义以及绝对值，牢记“只含有一个未知数，并且未知数的最高次数是的整式方程叫一元二次方程”是解题的关键．
 

13.【答案】 

【解析】解：转盘停止后，指针落在区域的概率是，
故答案为：．
转盘停止后，指针落在区域的概率是区的圆心角所占的比例，代入数据求解即可．
本题主要考查几何概率，随机事件的概率事件可能出现的结果数所有可能出现的结果数．
 

14.【答案】 

【解析】解：连接、，
四边形是正六边形，
，，，
，
，
的长度的长度为，
故答案为：．
连接、，根据正六边形的性质求出，的度数，再利用弧长公式可得答案．
本题主要考查了正六边形的性质，弧长的计算，熟练掌握正六边形的性质是解题的关键．
 

15.【答案】 

【解析】解：在矩形中，，，，
，
根据折叠可知，，
，
，
设，
，，
，，
在中，根据勾股定理，得，
解得，
，
故答案为：．
根据矩形的性质可得，，，根据平行线的性质可得，进一步可得，设，在中，根据勾股定理列方程，求出的长，根据进一步求解即可．
本题考查了翻折变换折叠问题，矩形的性质，解直角三角形，熟练掌握折叠的性质和矩形的性质是解题的关键．
 

16.【答案】 

【解析】解：如图，过点作于点，过点作于点，

则，
，
，
，
，
，
，
，
设，
，，
，，
，，
在中，由勾股定理得：，
即，
解得：负值已舍去，
，
，
故答案为：．
过点作于点，过点作于点，由含角的直角三角形的性质得，则，再由锐角三角函数定义得，，，则，，然后在中，由勾股定理得出方程，求出，则，即可解决问题．
本题考查了解直角三角形，熟练掌握锐角三角函数定义和勾股定理，正确作出辅助线构造直角三角形是解题的关键．
 

17.【答案】解：如图，为所作．
 

【解析】先作，再在上截取，然后过点作的垂线，垂足为点，则满足条件．
本题考查了作图复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
 

18.【答案】解：原式

．
，
由得：，
由得：，
不等式组的解集为：． 

【解析】根据分式的加减运算以及乘除运算法则即可求出答案．
根据一元一次不等式的解法即可求出答案．
本题考查分式的混合运算以及一元一次不等式组的解法，解题的关键是熟练运用一元一次不等式组的解法、分式的加减运算以及乘除运算法则，本题属于基础题型．
 

19.【答案】解：画树状图如下：

共有种等可能的结果，其中抽到的两张卡片恰好是“共享出行”和“共享知识”，即和的结果有种，
抽到的两张卡片恰好是“共享出行”和“共享知识”的概率为． 

【解析】画树状图得出所有等可能的结果数以及抽到的两张卡片恰好是“共享出行”和“共享知识”的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
 

20.【答案】   

【解析】解：根据扇形统计图可知，组女生所占百分比为，组女生所占百分比为，即，
组男生人数为，补全条形统计图如下：

由条形统计图可知，男生的中位数在组，将名男生上周平均每天体育锻炼时间从高到低排列，排在第，的两个数据为：，，
其中位数，
故答案为：，；
男生上周锻炼情况更好．
理由：男生上周平均每天体育锻炼时间的中位数、众数均大于女生；
人，
答：估计该校上周平均每天校外体育锻炼时间在分钟以上含分钟的学生一共有人．
求出组女生所占百分比，根据百分比之和为即可求得组女生所占百分比，根据频数之和为求得组的人数，即可补全条形统计图，根据中位数的定义可得的值；
平均数相同，根据中位数，众数比较即可得出结论；
用样本估计总体即可．
本题考查了扇形统计图，条形统计图，中位数、众数、平均数的定义，样本估计总体，理解题意，熟练掌握各个统计数据的计算方法，并灵活运用是解题的关键．
 

21.【答案】    

【解析】解：【解决问题】的外接圆半径为，连接并延长交于点，连接，则，
为的直径，
，
在中，
，
．
故答案为：，；
【结论应用】，，
，
，
，
外接圆的面积为．
故答案为：．
【解决问题】连接并延长交于点，连接，由圆周角定理得出，由正弦的定义可得出答案；
【结论应用】求出外接圆的半径，则可得出答案；
本题是圆的综合题，考查了锐角三角函数的定义，三角形的外接圆，圆周角定理，熟练掌握锐角三角函数的定义是解题的关键．
 

22.【答案】解：过点作于点，交于点，过点作于点，交于点，
四边形、四边形、四边形都是矩形，
，，，
设，
，
，
，
由勾股定理可知：，
，
由题意可知：，
在中，，
，
，
解得：，
，，，
由勾股定理可知：，
．
答：车向右移动的距离． 

【解析】过点作于点，交于点，过点作于点交于点，所以四边形、四边形、四边形都是矩形，设，根据锐角三角函数的定义以及勾股定理可求出的值，从而可求出的长度．
本题考查解直角三角形的应用，解题的关键是熟练运用矩形的性质、锐角三角函数的定义，本题属于中等题型．
 

23.【答案】证明：，，
四边形为平行四边形；
解：添加，使得四边形为菱形，理由如下：
四边形是平行四边形，
，，
又，
，
平行四边形是菱形． 

【解析】由两组对边分别平行的四边形是平行四边形可证四边形为平行四边形；
由菱形的判定定理可得结论．
本题考查了菱形的判定，平行四边形的判定和性质，掌握菱形的判定是解题的关键．
 

24.【答案】解：设，则，
，，
一次函数的图象经过点，
，解得，
，
把代入反比例函数得：，
反比例函数解析式为；
由，解得或，
，
，
，
的面积和的面积相等，
，即，
，
或． 

【解析】设，则，可得，把点代入一次函数解析式即可求出的值，进而表示出点的坐标，利用待定系数法求解析式即可；
将一次函数和反比例函数联立求出点的坐标，利用面积公式求得的面积，根据题意点在轴上，的面积和的面积相等，可得到，求得的长，进而求得点的坐标．
本题考查的是反比例函数与一次函数的交点问题，涉及到待定系数法求解析式、三角形面积以及求函数交点坐标，能够数形结合是解题的关键．
 

25.【答案】解：抛物线经过点，，
对称轴是：直线，
顶点坐标为，
设甲运动员空中运动轨迹抛物线的关系式为：，
将代入得：，
，
甲运动员空中运动轨迹抛物线的关系式为：；
根据题意可得，当时，即，
解得：，舍，
则，
所以甲运动员本次比赛得分为分． 

【解析】利用待定系数法可得结论；
根据题意知，是求水平距离的，即把时对应的值求出取正数值，代入到总分的式子即可算出．
本题主要考查了二次函数的应用，解题关键：一是要会用待定系数法求解析式，二是会求与轴的交点．
 

26.【答案】解：当点在的垂直平分线上时，，
则有，
解得；
，，，
，
四边形是平行四边形，
，
，
，
，
解得．
经检验是分式方程的解．
满足条件的的值为；
如图中，过点作于点．

，
，
，
，
，
，
时，有最大值，最大值为；
如图，，，
，
当时，过点作于点．

由题意，，，，
，
，
解得．
满足条件的的值为． 

【解析】根据，构建方程求解；
由，推出，由此构建方程求解；
利用三角形面积公式构建二次函数，利用二次函数的性质求解；
说明，当时，过点作于点根据，构建方程求解．
本题属于四边形综合题，考查了平行四边形的判定和性质，动点问题，三角形的面积，解直角三角形等知识，解题的关键是理解题意，学会利用参数构建方程解决问题．