2022-2023学年浙江省杭州市下城区采荷中学七年级（下）期中数学试卷（含解析）

这是一份2022-2023学年浙江省杭州市下城区采荷中学七年级（下）期中数学试卷（含解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年浙江省杭州市下城区采荷中学七年级（下）期中数学试卷一、选择题（本题共10小题，共30分）1.  下列由左到右边的变形中，是因式分解的是(    )A.  B.
C.  D. 2.  下列多项式乘法中，能用平方差公式计算的是(    )A.  B.
C.  D. 3.  已知，则等于(    )A.  B.  C.  D. 4.  下列图形中，与不是同位角的是(    )A.  B.
C.  D. 5.  计算的结果是(    )A.  B.  C.  D. 6.  如图所示，在下列四组条件中，不能判定的是(    ) A.  B.
C.  D. 7.  九章算术是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步问：人与车各几何？译文：若人坐一辆车，则两辆车是空的；若人坐一辆车，则人需要步行，问：人与车各多少？设有辆车，人数为，根据题意可列方程组为(    )A.  B.  C.  D. 8.  若，，则的值为(    )A.  B.  C.  D. 9.  已知关于、的二元一次方程，当每取一个值时，就有一个方程，而这些方程有一个公共解，这个公共解是(    )A.  B.  C.  D. 10.  设，，，则，，的大小关系是(    )A.  B.  C.  D.  二、填空题（本题共7小题，共28分）11.  分解因式： ______ ．12.  下列各组数：，，，中，______是方程的解；______是方程的解；______是方程组的解．填序号13.  如图，是由平移得到的，且、、、在同一条直线上，若，，则的长度为______ ．
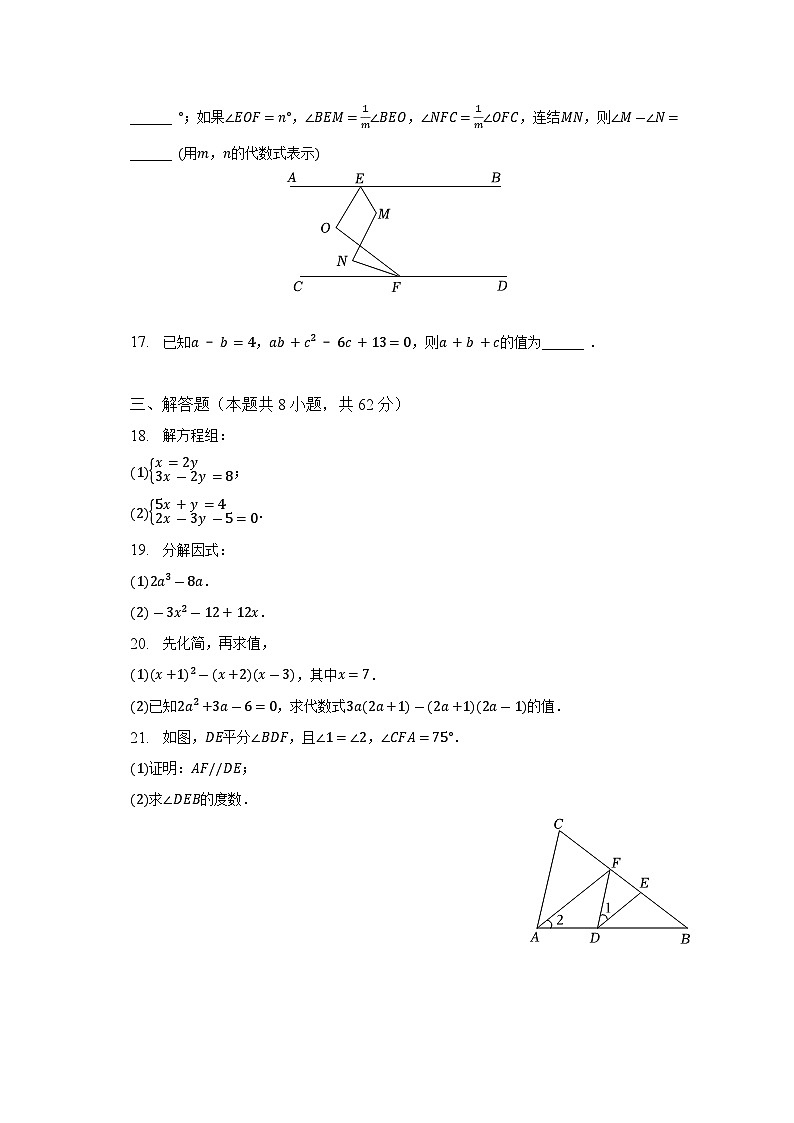
14.  若多项式是完全平方式，则常数的值为          ．15.  已知，，则的值是______ ．16.  如图，已知，点，分别在直线，上，点在直线，之间，如所示，分别在和的平分线上取点，，连结，则 ______ ；如果，，，连结，则 ______ 用，的代数式表示
17.  已知，，则的值为______ ． 三、解答题（本题共8小题，共62分）18.  解方程组：
；             
．19.  分解因式：
．
．20.  先化简，再求值，
，其中．
已知，求代数式的值．21.  如图，平分，且，．
证明：；
求的度数．
22.  阅读理解并解答：
我们把多项式和叫做完全平方式，在运用完全平方公式进行因式分解时，关键是判断一个多项式是不是一个完全平方式同样地，把一个多项式进行部分因式分解可以解决求代数式值的最大最小值问题：
例如：．
，．
则代数式的最小值为______ ，此时，相应的的值为______ ．
．
．
，．
代数式的最小值为______ ，此时，相应的的值为______ ．
仿照上述方法，代数式有最______ “大”或“小”值，并求相应的代数式的最值．23.  两个边长分别为和的正方形如图放置图，其阴影部分面积为；两个边长分别为和的正方形如图放置图，其阴影部分面积为．

用含，的代数式表示；
当，时，求的值；
当，时，求出图中的阴影部分的面积．24.  某工厂准备用图甲所示的型正方形板材和型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．
若现有型板材张，型板材张可制作竖式和横式两种无盖箱子各多少个？
若该工厂准备用元资金去购买，两种型号板材，制作竖式，横式箱子共个，已知型板材每张元，型板材每张元，发现资金恰好用完，问可以制作竖式箱子多少个？
若该工厂新购得张规格为的型正方形板材，将其全部切割成型或型板材不记损耗，用切割的板材制作成两种类型的箱子，要求竖式箱子不少于个，且材料恰好用完，则最多可以制作竖式箱子多少个？
 25.  将一副三角板中的两块直角三角板如图放置，，，，，．

若三角板如图摆放时，则        ，        ；
现固定的位置不变，将沿方向平移至点正好落在上，如图所示，与交于点，作和的角平分线交于点，求的度数；
现固定，将绕点顺时针旋转至与直线首次重合的过程中，当线段与的一条边平行时，则        直接写出答案
答案和解析 1.【答案】 【解析】解：、，是整式的乘法，不是因式分解，故本选项不合题意；
B、，是分式，不是整式，不是因式分解，故本选项不合题意；
C、，没把一个多项式转化成几个整式积的形式，不是因式分解，故本选项不合题意；
D、，把一个多项式转化成几个整式积的形式，是因式分解，故本选项符合题意；
故选：．
根据因式分解是把一个多项式转化成几个整式积的形式，可得答案．
此题主要考查了因式分解的意义．正确把握因式分解的定义是解题的关键．
 2.【答案】 【解析】解：．和，和不分别相同，不符合平方差公式，故本选项不符合题意；
B.，不符合平方差公式，故本选项不符合题意；
C.，符合平方差公式，故本选项符合题意；
D.

，不符合平方差公式，故本选项不符合题意；
故选：．
根据平方差公式的特点逐个判断即可．
本题考查了平方差公式和完全平方公式，能熟练掌握平方差公式是解此题的关键，．
 3.【答案】 【解析】解：，
得：，
则．
故选：．
方程组两方程相加即可求出所求．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 4.【答案】 【解析】解：根据同位角的定义可知选项C中的和不是同位角，
故选：．
根据同位角的定义即可得到结论．
本题考查了同位角、内错角、同旁内角，熟记定义是解题的关键．
 5.【答案】 【解析】解：

．
故选：．
利用单项式乘单项式的法则进行运算即可．
本题主要考查单项式乘单项式，解答的关键是对相应的运算法则的掌握．
 6.【答案】 【解析】解：、当时，，本选项不符合题意；
B、当时，，本选项不符合题意；
C、当时，，本选项不符合题意；
D、当时，，本选项符合题意．
故选：．
根据平行线的判定方法分别对四个选项进行判断．
本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
 7.【答案】 【解析】解：设共有人，辆车，
依题意得：．
故选：．
设共有人，辆车，根据“如果每人坐一辆车，那么有辆空车；如果每人坐一辆车，那么有人需要步行”，即可得出关于，的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组以及数学常识，找准等量关系，正确列出二元一次方程组是解题的关键．
 8.【答案】 【解析】解：，
，
，
，
，
，
．
故选：．
由得，，两边平方求出的值，代入原式即可得结果．
本题考查了完全平方公式，整体代入法，熟练掌握公式并进行变形应用是解题关键．
 9.【答案】 【解析】解：原方程可整理得：
，
根据题意得：
，
解得，
故选：．
把原方程整理得：，根据“当每取一个值时就有一个方程，而这些方程有一个公共解”，可知这个公共解与无关，得到关于和的二元一次方程组，解之即可．
本题考查了二元一次方程组的解，正确掌握解二元一次方程组是解题的关键．
 10.【答案】 【解析】解：．
故答案为：．
直接提取公因式，进而分解因式即可．
此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
 11.【答案】     【解析】解：，
、互为相反数，
，，，中，是方程的解的是；
把代入方程得：左边，右边，左边右边，所以是方程的解，
把代入方程得：左边，右边，左边右边，所以是方程的解，
把代入方程得：左边，右边，左边右边，所以是方程的解，
把代入方程得：左边，右边，左边右边，所以不是方程的解，
即是方程的解；
是方程组的解，
故答案为：，，．
代入方程，看看是否两边相等即可，根据二元一次方程组的解的定义得出即可．
本题考查了二元一次方程的解和二元一次方程组的解，能理解二元一次方程的解和二元一次方程组的解的定义是解此题的关键．
 12.【答案】 【解析】解：由平移的性质可知，，
，，
，
故答案为：．
根据平移的性质得到，结合图形计算，得到答案．
本题考查的是平移的性质，根据平移的性质得到是解题的关键．
 13.【答案】 【解析】解：是完全平方式，
，
，
解得，
故答案为：．
【分析】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．
利用完全平方公式的结构特征判断即可确定出的值．  14.【答案】 【解析】解：，，
，
，
，



．
故答案为：．
由题意可求得，再把相应值代入运算即可．
本题主要考查幂的乘方，解答的关键是对相应的运算法则的掌握．
 15.【答案】  【解析】解：过点作，过点作，过点作，如图：

，，
，
，，
，
即，
，
，
平分，平分，
设，，
，
，
，
，，，
，
，，，



，
的值为．
，，
，
，，
，
即，
，
，
，，
，，，
，
，，，





；
的值为．
故答案为：，．
过点作，易得，过点作，过点作，由角平分线的定义可设，，由可求，进而求解．
本题主要考查平行线的性质，角平分线的定义，灵活运用平行线的性质是解题的关键．
 16.【答案】解：，
将代入得：，即，
将代入得：，
则方程组的解为；
，
得：，即，
将代入得：，
则方程组的解为． 【解析】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
方程组利用代入消元法求出解即可；
方程组利用加减消元法求出解即可．
 17.【答案】解：原式
；

原式
． 【解析】先提取公因式，再利用平方差公式分解因式即可；
直接提取公因式，再利用完全平方公式分解因式即可．
此题主要考查了提取公因式法以及公式法分解因式，正确运用公式法分解因式是解题关键．
 18.【答案】解：原式，
当时，原式；
原式，
由，得到，
则原式． 【解析】原式利用完全平方公式，以及多项式乘以多项式法则计算，去括号合并得到最简结果，把的值代入计算即可求出值；
原式利用单项式乘以多项式，平方差公式计算，去括号合并后，将已知等式变形后代入计算即可求出值．
此题考查了整式的混合运算化简求值，熟练掌握运算法则是解本题的关键．
 19.【答案】证明：平分，
，
，
，
；
解：，
，
，
的度数为． 【解析】利用角平分线的定义可得，从而利用等量代换可得，然后利用平行线的判定即可解答；
利用的结论可得，然后利用平角定义进行计算，即可解答．
本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．
 20.【答案】        大 【解析】解：

，
代数式的最小值为，相应的的值为；
故答案为：，；
，
代数的最小值为，相应的的值为；
故答案为：，；

，
代数的最大值为，此时，相应的的值为．
故答案为：大．
根据材料给出的结论直接求出代数式的最小值及相应的的值；
根据材料给出的结论直接求出代数式的最小值及相应的的值；
先提取负号再配成完全平方形式，从而确定代数式的最小值及相应的的值．
本题考查了因式分解的应用、偶次方具有非负性、完全平方式，熟练掌握完全平方式结构特点，配方是解题的关键．
 21.【答案】解：；
，，
；
，，





． 【解析】根据正方形的面积公式求解；
先分解因式，再整体代入求解；
先用，表示，再变形代入求解．
本题考查了完全平方公式的几何背景，整体代入求值是解题的关键．
 22.【答案】解：设可制作竖式无盖箱子个，可制作横式无盖箱子个，
由题意得：，
解得：，
答：可制作竖式无盖箱子个，可制作横式无盖箱子个；
设可以制作竖式箱子个，则制作横式箱子个，
由题意得：，
解得：，
答：可以制作竖式箱子个；
型可以看成三列，每一列可以做成个型或个型，个型就有列，

材料恰好用完，
最后型的数量一定是的倍数，
设可以制作竖式箱子个，制作横式箱子个，
个竖式无盖箱子需要个型和个型，个横式无盖箱子需要个型和个型，个型相当于个型，
，
，
、均为整数，，
，，，，
答：最多可以制作竖式箱子个． 【解析】设可制作竖式无盖箱子个，可制作横式无盖箱子个，由题意：现有型板材张，型板材张，列出二元一次方程组，解方程组即可；
设可以制作竖式箱子个，则制作横式箱子个，由题意：用元资金去购买，两种型号板材，列出一元一次方程，解方程即可；
型可以看成三列，每一列可以做成个型或个型，个型就有列，则最后型的数量一定是的倍数，设可以制作竖式箱子个，制作横式箱子个，由题意列出二元一次方程，即可解决问题．
本题考查了二元一次方程组的应用、一元一次方程的应用以及二元一次方程的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；找准等量关系，正确列出一元一次方程；找准等量关系，正确列出二元一次方程．
 23.【答案】 【解析】解：

，

，

，
，
．
故选：．
根据乘法分配律可求，将变形为，再注意整体思想进行计算，根据提取公因式、完全平方公式和算术平方根可求，再比较大小即可求解．
本题考查了因式分解的应用，熟记乘法分配律、完全平方公式的结构特点是解题的关键．注意整体思想的运用．
 24.【答案】 【解析】解：，
，
，
，
，
，
，，
解得，，
，


．
故答案为：．
首先根据，可得，再根据，应用完全平方公式，求出、的值，进而求出的值，然后把、、相加，求出的值即可．
此题主要考查了因式分解的应用，解答此题的关键是要明确完全平方公式并能正确应用．
 25.【答案】    或或 【解析】解：，
，
，
、、三点共线，
；
故答案为：；；
，
，
，
，分别平分和，
，，
；
当时，如图，

，，，
，
，
，
；
当时，如图，

此时，
；
当时，如图，

此时，，，
．
综上所述，的度数为或或．
故答案为：或或．
根据平行线的性质和三角板的角的度数解答即可；
根据平行线的性质和角平分线的定义解答即可；
分当时，当时，当时，三种情况进行解答即可．
本题考查了旋转的性质，角平分线的定义，平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用，理清各角度之间的关系是解题的关键，也是本题的难点．