2023届陕西省宝鸡市中考数学阶段性适应模拟试题（一模）含解析

展开

这是一份2023届陕西省宝鸡市中考数学阶段性适应模拟试题（一模）含解析，共14页。试卷主要包含了17 4等内容，欢迎下载使用。

2023届陕西省宝鸡市中考数学阶段性适应模拟试题（一模）

题号	一	二	三	总分
得分

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

一、选择题（本大题共8小题，共24分。在每小题列出的选项中，选出符合题目的一项）

在实数，，，，中，无理数的个数是( )

A. 个 B. 个 C. 个 D. 个

一个正方体的每一个面都有一个汉字，其平面展开图如图所示，那么在该正方体中和“好”字相对的字是( )

A. 共 B. 创 C. 美 D. 园

若定义表示，表示，则运算的结果为( )

A. B. C. D.

适合下列条件的中，直角三角形的个数为( )
：：：：；；；．

A. B. C. D.

已知关于的一次函数的图象经过第一、二、四象限，则代数式可化简为( )

A. B. C. D.

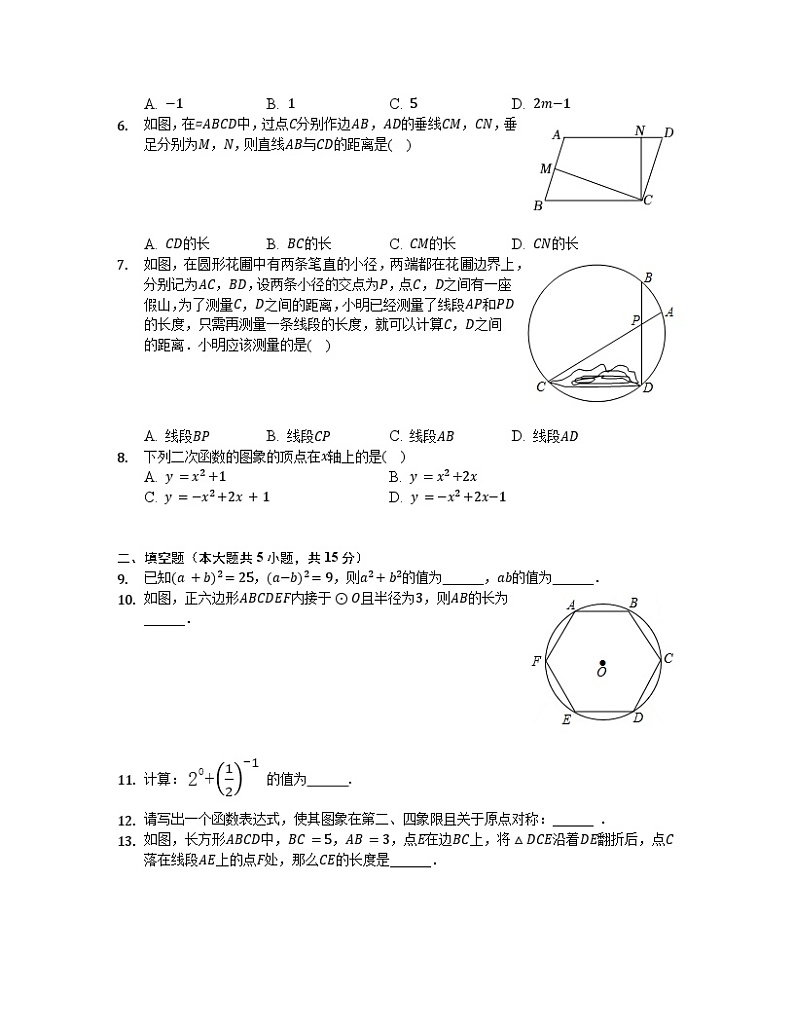
如图，在▱中，过点分别作边，的垂线，，垂足分别为，，则直线与的距离是( )

A. 的长 B. 的长 C. 的长 D. 的长

如图，在圆形花圃中有两条笔直的小径，两端都在花圃边界上，分别记为，，设两条小径的交点为，点，之间有一座假山，为了测量，之间的距离，小明已经测量了线段和的长度，只需再测量一条线段的长度，就可以计算，之间的距离．小明应该测量的是( )

A. 线段 B. 线段 C. 线段 D. 线段

下列二次函数的图象的顶点在轴上的是( )

A. B.
C. D.

二、填空题（本大题共5小题，共15分）

已知，，则的值为______，的值为______．
如图，正六边形内接于且半径为，则的长为______．

计算：的值为　　　　
请写出一个函数表达式，使其图象在第二、四象限且关于原点对称：______ ．
如图，长方形中，，，点在边上，将沿着翻折后，点落在线段上的点处，那么的长度是______．

三、解答题（本大题共13小题，共81分。解答应写出文字说明，证明过程或演算步骤）

本小题分
计算：；
解不等式组并求其整数解．．
本小题分
解不等式组：，并在数轴上表示它的解集．
本小题分
化简：
本小题分
如图，在中，，是的中点，垂直平分，交于点，交于点，是直线上的动点．
当时．
若，则点到的距离为______；
若，，求的周长；
若，且的面积为，则的周长的最小值为______．

本小题分
如图，在▱中，是对角线上的一点，过点作，且，连接，，．
求证：≌．
若，，，求的长．

本小题分
根据21年月份的月历表，思考并回答如下问题：
年月日是星期几；
月日是星期六，在年的月历中，日恰好也是星期六的月份有哪个；
有一种计算机病毒叫做黑色星期五，当计算机的日期是日又是星期五时，这种病毒就发作．已知年月日是黑色星期五，请找出来接下来的三个“黑色星期五”．

本小题分
在一个不透明的袋中装有个黄球，个黑球和个红球，它们除颜色外其他都相同．
将袋中的球摇匀后，求从袋中随机摸出一个球是黄球的概率；
若向这个袋子加入个红球，从袋中随机摸出一个球，求摸到不是红球的概率．
本小题分
如图，在楼房前有两棵树与楼房在同一直线上，且垂直于地面，为了测量树、的高度，小明爬到楼房顶部处，光线恰好可以经过树的顶站点到达树的底部点，俯角为，此时小亮测得太阳光线恰好经过树的顶部点到达楼房的底部点，与地面的夹角为，树的影长为米，请求出树、的高度．结果保留根号

本小题分
桃溪中学拟计划招收学科优秀特长生，成立四种学科竞赛班：语文、数学、理化、政史．为了设置各学科班数，校教导处对各科优秀学生报名活动意向进行调查，随机抽取了部分学生，并将调查结果绘制成图，图两幅不完整的统计图，请结合图中信息解答下列问题：
本次共调查了______名学生；
将图的统计图补充完整并求出数学在图中所对的圆心角的度数；
已知在被调查的准备报名“理化”科目的个学生中只有名女生，现从这名学生中任意抽取名学生参加座谈听取建议，请用画树状图或列表的方法，求出恰好抽到一名男生一名女生的概率．

本小题分
甲，乙两车从地驶向地，并以各自的速度匀速行驶，甲车比乙车早行
驶，并且甲车途中休息了甲车休息前后的速度相同，甲、乙两车行驶的路程与行驶的时间的函数图象如图所示．
求、的值；
求甲车比乙车晚多少小时到达地；
两车相距时乙车行驶了多少小时．

本小题分
如图，与直线相离，于点，交于点，过点作的切线，切点为，连接交直线于点
求证：；
若，的半径为，求的长．

本小题分
如图，抛物线与轴交于点，抛物线经过点，点是轴上一动点．

求此抛物线的函数表达式；
抛物线上是否存在点，使得以，，，为顶点的四边形是平行四边形？若存在，请求出所有满足条件的点的坐标；若不存在，请说明理由．
本小题分
有这样一个问题：

如图，的内切圆与斜边相切于点，，，
求的面积用含，的式子表示．
小冬根据学习几何的经验，先从特殊情况开始探究：
解：如图，令，，
设的内切圆分别与、相切于点、，的长为．
根据切线长定理，得，，．
根据勾股定理得，．
整理，得
所以
请你参考小冬的做法．
解决以下问题：当，时，求的面积；
当，时，直接写出求的面积用含，的式子表示为______．

答案解析

10.

11.

12.答案不唯一

13.

14.解：原式
；
，解得，
不等式组的解集是，
整数解是，，，．

15.解：解不等式，得：，
解不等式，得：，
则不等式组解集为，
将解集表示在数轴上如下：

16.解：

．

17.

18.证明：四边形是平行四边形，
，，
，
，
，

解：，且，
四边形是平行四边形，
，，
四边形是平行四边形，
，，
，，
四边形是平行四边形，
，
≌，
，
，
，
，
，
，
．

19.解：天
星期天
年月日是星期四；
年月日是星期三，
年月日是星期六，
年月日是星期六，
年月日是星期二，
年月日是星期四，
年月日是星期日，
年月日是星期二，
年月日是星期五，
年月日是星期一，
年月日是星期三，
年月日是星期六，
年月日是星期一，
故在年的月历中，日恰好也是星期六的月份有月月月；
年月日是黑色星期五，年月日是黑色星期五，年月日是黑色星期五．

20.解：不透明的袋中装有个黄球，个黑球和个红球，
从袋中随机摸出一个球是黄球的概率是；
向这个袋子加入个红球，
红球共有个球，球的总数为个，
从袋中随机摸出一个球，摸到不是红球的概率．

21.解：在中，
，
，
，
，
，
在中，，
，
树高是米，树高是米．

22.

23.解：由题意得，
甲小时距出发地，
甲速度为，
，
答：，；
设甲车休息后与之间的函数关系式为，把，代入得：
，解得，
甲车休息后与之间的函数关系式为，
当时，，
解得，
甲车小时到达地，
设乙车行驶的路程与时间之间的解析式为，把，代入得：
，解得，
乙车行驶的路程与时间之间的解析式为，
当时，，
解得，
乙车到达的时间是小时，
甲车比乙车晚小时到达地；
当时，
解得：，
此时乙车行驶了小时，
当时，
解得：，
此时乙车行驶了小时；
当乙已经到地后，，
解得，
此时乙车行驶了小时，
当乙车出发小时或小时或小时后，两车相距．