青海省海东市2023届高三第三次联考数学（文科）试题(含答案)

这是一份青海省海东市2023届高三第三次联考数学（文科）试题(含答案)，共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
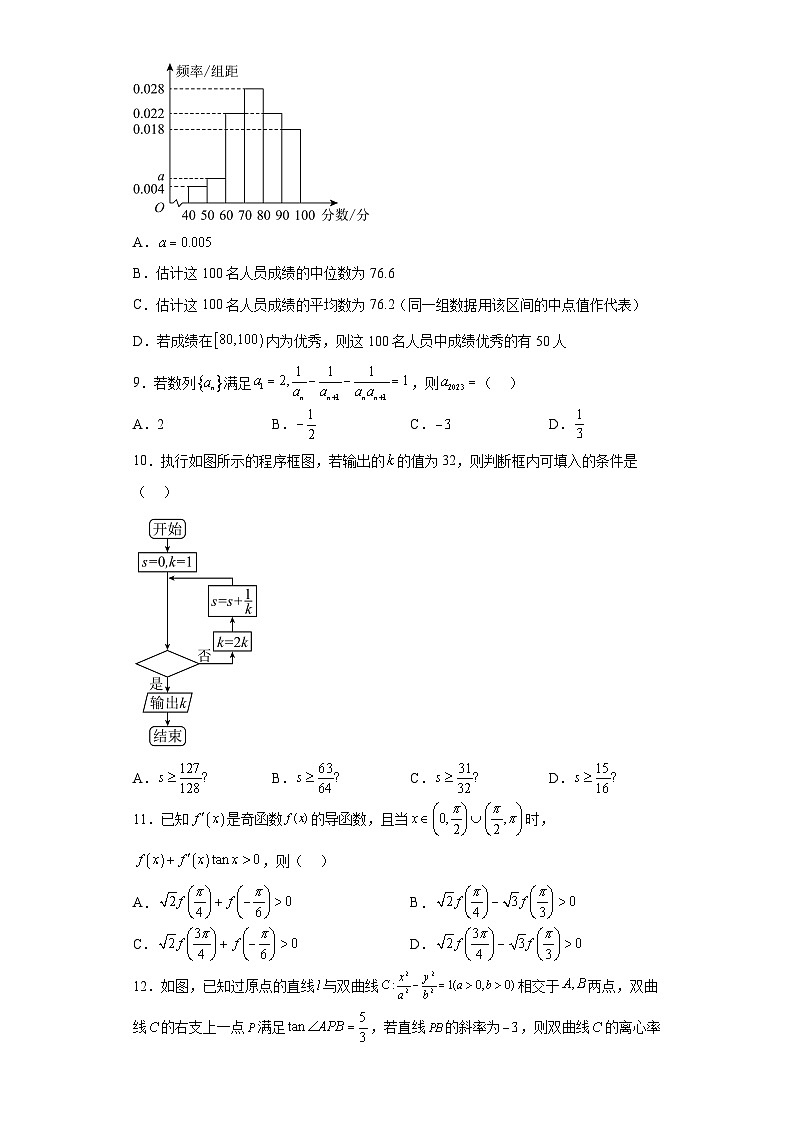
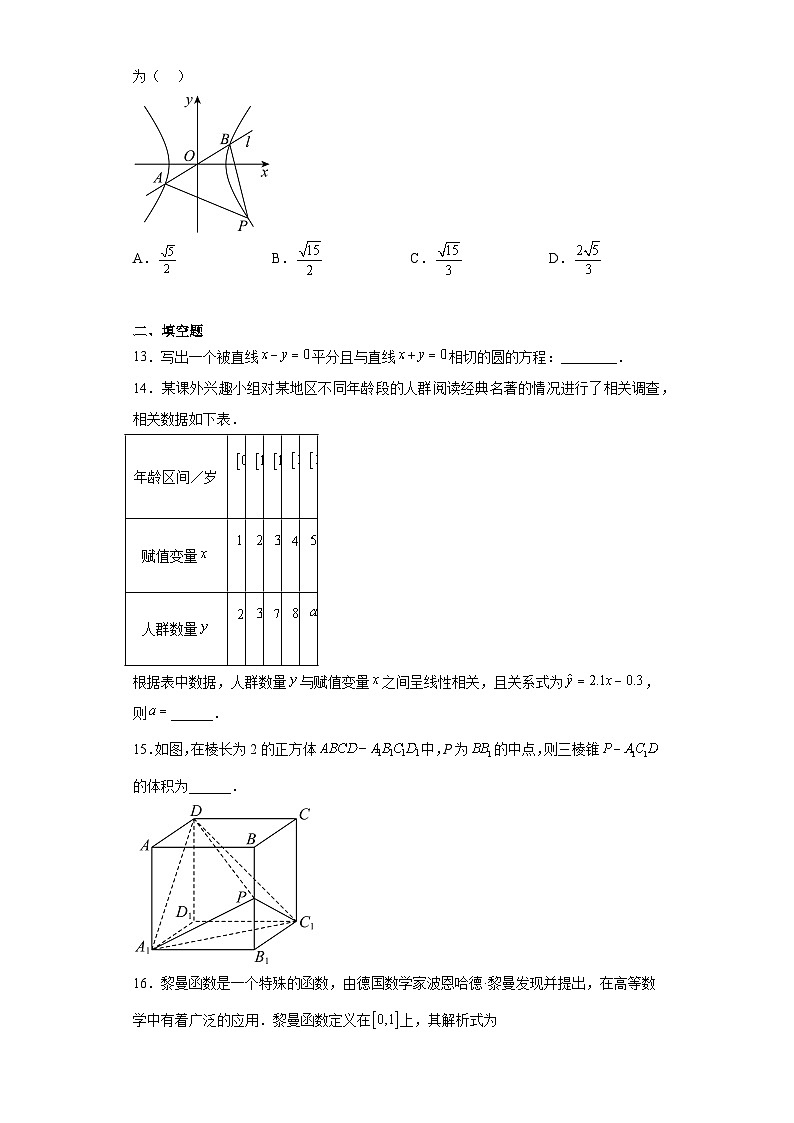
青海省海东市2023届高三第三次联考数学（文科）试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．集合，，则（    ）A． B． C． D．2．已知，则复数z在复平面内对应的点位于（    ）A．第一象限 B．第二象限 C．第三象限 D．第四象限3．l，m是两条不重合的直线，，是两个不重合的平面，若，，则“l//m”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件4．设等差数列的前n项和为，若，则（    ）A．44 B．48 C．55 D．725．已知向量，，若，则（    ）A．0 B．C．1 D．26．图中是抛物线形拱桥，当水面在时，拱顶距离水面2米，水面宽度为8米，则当水面宽度为10米时，拱顶与水面之间的距离为（    ）A．米 B．米 C．米 D．米7．为了得到函数的图象，只需将函数的图象（    ）A．向左平移个单位长度 B．向右平移个单位长度C．向左平移个单位长度 D．向右平移个单位长度8．某单位组织开展党史知识竞赛活动，现把100名人员的成绩（单位：分）绘制成频率分布直方图（每组数据均左闭右开），则下列各选项正确的是（    ）A．B．估计这100名人员成绩的中位数为76.6C．估计这100名人员成绩的平均数为76.2（同一组数据用该区间的中点值作代表）D．若成绩在内为优秀，则这100名人员中成绩优秀的有50人9．若数列满足，则（    ）A．2 B． C． D．10．执行如图所示的程序框图，若输出的的值为32，则判断框内可填入的条件是（    ）  A． B． C． D．11．已知是奇函数的导函数，且当时，，则（    ）A． B．C． D．12．如图，已知过原点的直线与双曲线相交于两点，双曲线的右支上一点满足，若直线的斜率为，则双曲线的离心率为（    ）A． B． C． D． 二、填空题13．写出一个被直线平分且与直线相切的圆的方程：________．14．某课外兴趣小组对某地区不同年龄段的人群阅读经典名著的情况进行了相关调查，相关数据如下表．年龄区间／岁赋值变量人群数量根据表中数据，人群数量与赋值变量之间呈线性相关，且关系式为，则______．15．如图，在棱长为2的正方体中，P为的中点，则三棱锥的体积为______．  16．黎曼函数是一个特殊的函数，由德国数学家波恩哈德·黎曼发现并提出，在高等数学中有着广泛的应用．黎曼函数定义在上，其解析式为，若函数是定义在上的奇函数，且对任意的，都有，当时，，则______． 三、解答题17．在中，内角的对边分别为，且．(1)求角的值；(2)若，求边上的中线的最大值．18．清明期间，某校为缅怀革命先烈，要求学生通过前往革命烈士纪念馆或者线上网络的方式参与“清明祭英烈”活动，学生只能选择一种方式参加.已知该中学初一、初二、初三3个年级的学生人数之比为，为了解学生参与“清明祭英烈”活动的方式，现采用分层抽样的方法进行调查，得到如下数据. (1)求，的值；(2)从该校各年级被调查且选择线上网络方式参与“清明祭英烈”活动的学生人任选两人，求这两人是同一个年级的概率.19．如图，四棱锥的底面是等腰梯形，，，，底面ABCD，为棱上的一点.(1)证明：；(2)若三棱锥的体积为，求的值.20．已知椭圆（a>0，b>0）的右焦点F在直线上，A，B分别为C的左、右顶点，且．(1)求C的标准方程；(2)过点的直线l与C交于P，Q两点，线段PQ的中点为N，若直线AN的斜率为，求直线l的斜率．21．已知函数．(1)若，求的图象在处的切线方程；(2)若恒成立，求的取值范围．22．在直角坐标系中，曲线的参数方程为 （为参数）．以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为．(1)求曲线的普通方程和直线的直角坐标方程；(2)若曲线与直线有两个公共点，求的取值范围．23．已知函数(1)求不等式的解集；(2)若的最大值为，且正数，满足，求的最小值．
参考答案：1．C2．D3．D4．A5．C6．D7．B8．C9．B10．C11．A12．C13．（答案不唯一，符合题意即可）14．15．216．/17．(1)(2) 18．(1)，(2) 19．(1)证明见解析(2) 20．(1)(2) 21．(1)(2) 22．(1)，(2) 23．(1)(2)3