2023届安徽省滁州市中考数学阶段性适应模拟试题（4月）无答案

这是一份2023届安徽省滁州市中考数学阶段性适应模拟试题（4月）无答案，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
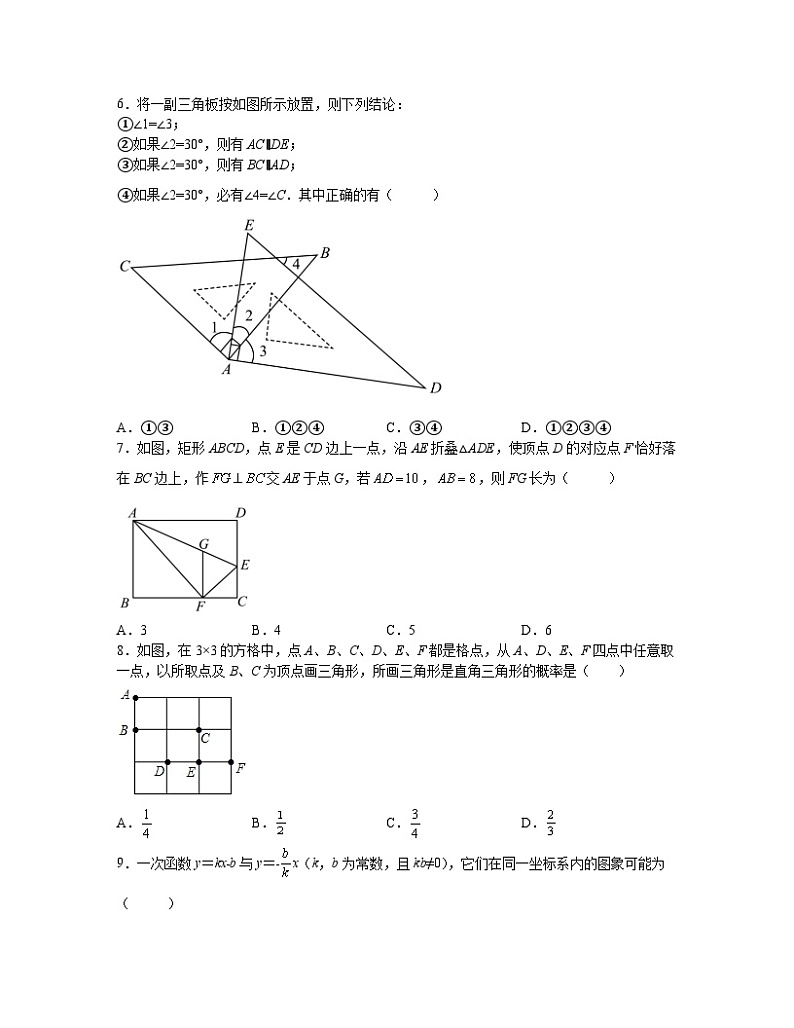
2023届安徽省滁州市中考数学阶段性适应模拟试题（4月）  第I卷（选择题 40分） 一、选择题（本大题共10小题，每小题4分，满分40分）1．下列各数：，，，，，其中是负数的有（       ）A．2个 B．3个 C．4个 D．5个2．地球不是沿着一个完美的圆形轨道环绕太阳旋转，所以日地距离不是一个常数．不过，地球的公转轨道是一个偏心率很低的椭圆形，接近于圆形．1976年国际天文学联合会把它确定为149597870千米，约1.5亿公里，将1.5亿用科学记数法表示应为（     ）A．15×108km B．1.5×108km C．15×107km D．1.5×109km3．下列如图所示的立体图形的俯视图是（       ）A． B． C． D．4．下列运算中，正确的是（　　）A． B．C．a2+2a3＝2a5 D．（﹣2a2）3＝﹣6a65．甲、乙两人相约从A地到B地，甲骑自行车先行，乙开车，两人均同一路线上速匀行驶，乙到B地后即停车等甲．甲、乙两人之间的距离y（千米）与甲行驶的时间x（小时）之间的函数关系如图所示，则乙从A地到B地所用的时间为（　　）A．0.25小时 B．0.5小时 C．1小时 D．2.5小时6．将一副三角板按如图所示放置，则下列结论：①∠1=∠3；②如果∠2=30°，则有AC∥DE；③如果∠2=30°，则有BC∥AD；④如果∠2=30°，必有∠4=∠C．其中正确的有（       ） A．①③ B．①②④ C．③④ D．①②③④7．如图，矩形ABCD，点E是CD边上一点，沿AE折叠△ADE，使顶点D的对应点F恰好落在BC边上，作交AE于点G，若，，则FG长为（       ）A．3 B．4 C．5 D．68．如图，在3×3的方格中，点A、B、C、D、E、F都是格点，从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，所画三角形是直角三角形的概率是（　　）A． B． C． D．9．一次函数y＝kx﹣b与y＝﹣x（k，b为常数，且kb≠0），它们在同一坐标系内的图象可能为（       ）A． B．C． D．10．如图，点A1、A2依次在y＝（x＞0）的图象上，点B1，B2依次在x轴的正半轴上，若△A1OB1，△A2B1B2均为等边三角形，则点B2的坐标为（　　）A．（，0） B．（，0） C．（，0） D．（，0）第II卷（非选择题  110分）二、填空题（本大题共4小题，每小题5分，满分20分）11．不等式的解集是______.12．若关于x的过程有实数解，那么实数a的取值范围是_________.13．如图，点A是反比例函数y＝（x＞0）图象上的任意一点，过点A作垂直x轴交反比例函数y＝（x＞0）的图象于点B，连接AO，BO，若ΔABO的面积为1.5，则k的值为____________14．如图，已知点B在线段AC上，点E在线段BD上，∠ABD=∠DBC，AB=DB，EB=CB，M，N分别是AE，CD的中点，现有如下结论：①∠ABD=∠BDN；②MB=NB；③MB⊥NB；④S△ABM=S△BCN，其中正确的结论是_____（只填序号）．三、解答题15．（5分）计算：；16．（8分）如图，三角形ABC的顶点都在方格纸的格点上．将三角形ABC向左平移2格，再向上平移4格．（1）请在图中画出平移后的三角形A′B′C′；（2）若图中一小网格的边长为1，求三角形A′B′C′的面积．17．（8分）某公园有一块长方形空地如图所示（长度单位：m），阴影部分设计为草坪．（1）用整式表示草坪的面积；（2）若，，求草坪的面积18．（9分）观察下列等式＝1，＝，＝，将以上三个等式两边分别相加得：++＝1++=1（1）猜想并写出：＝        ． （2）直接写出下列各式的计算结果：①+++…+＝        ；②+++…+＝           ．（3）探究并计算：+++…+．19．（10分）如图是某户外看台的截面图，长的看台与水平地面的夹角为35°，与平行的平台长为，点F是遮阳棚上端E正下方在地面上的一点，测得，在挡风墙的点D处测得点E的仰角为26°，求遮阳棚的长（计算结果精确到十分位）．（参考数据：，，，）20．（12分）如图1，在⊙O中，AC为直径，D在上，B为中点，过B作BF⊥AD于F．（1）求证：BF为⊙O的切线；（2）如图2，连接DO并延长交AB于G，交⊙O于E，连接BE，若AG=AD=1，求DF．21．（10分）某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)，在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：（1）这次统计共抽查了_____名学生；（2）将条形统计图补充完整；（3）该校共有2000名学生，请估计该校最喜欢用“微信”进行沟通的学生有多少名？22．（14分）（1）感知：如图①.，，于点，于点．求证：；（2）拓展：如图②，点，在的边，上，点，在在内部的射线上，，分别是，的外角，已知，．求证：；（3）应用：如图③，在中，，，点在边上，，点，在线段上，．若的面积为12，则与的面积之和为______．23．（14分）二次函数图像与y轴交于点C，(1)如图，若二次函数图象与x轴交于点A，，①求二次函数的表达式；②点P为第二象限内抛物线上一点，连接BP、AC，交于点Q，令，请判断：是否有最大值？如有，请求出有最大值时点P的坐标；如没有，请说明理由．(2)若二次函数的顶点为M，连接MC，令MC与y轴的夹角为，当时，直接写出m的取值范围______．
答案 1．C   2．B   3．B   4．B   5．B   6．B   7．C  8．C   9．C    10．B11．    12．a≥-1    13．-2     14．②③④15．1解：，．16．（1）所作图形如图所示：（2）三角形A′B′C′的面积′=×4×4=8．17．（1）；（2）解：（1）草坪的面积为：．（2）当，时，草坪的面积为：．18．（1）；（2）①；②；（3）．解：（1）；故答案为；（2）①；②+++…+；故答案为①；②；（3）+++…+=.19．13.3m解：过点B作BH⊥AP于H，过D作DG⊥EF于G．则∠BHA=∠DGE=90°，由题意得：AB=15m，∠A=35°，∠EDG=26°，在Rt△BAH中，AH=AB•cos35°≈15×0.82=12.3（m），∴FH=AH-AF=12.3-2.3=10（m），GD=FH+BC=10+2=12（m），在Rt△EGD中，cos∠EDG==cos26°≈0.90，∴，答：遮阳棚DE的长约为13.3m．20．（1）证明：连接OB， ∴OB＝OA，∴∠2=∠3，∵B为中点，∴∠1=∠2，∴∠1=∠3，∴AF∥OB，∴∠OBF+∠F=，∵BF⊥AD，∴∠F=，∴∠OBF=，∴半径OB⊥BF于B，∴BF为⊙O的切线；（2）连接AE，延长BO交AE于H，连接DB，∵DE为直径，∴∠DAE=∠DBE=，∵AF∥BO，∴∠BHA=-∠DAH=，∴四边形AFBH为矩形，∴AH=BF，AF=BH，设DF=x，∴BH=AF=x+1，∵OH⊥AE于H，∴AH=EH，DO=EO，∴OH为△ADE中位线，∴OH=AD=，∴OB=BH-OH=x+，∵AF∥OB，∴∠4=∠7，∵AD=AG＝1，∴∠4=∠5，∵∠5=∠6，∴∠6=∠7，∴BG=OB=OA=x+，∴AB=BG+AG=x+，在Rt△AOH中，根据勾股定理得：，∴，在Rt△AFB中，根据勾股定理得：，即，解得：x=，∴DF=．21．解：（1）20÷20%＝100(人)；故100；（2）短信的人数为：100×5%＝5(人)，微信人数为：100﹣20﹣5﹣30﹣5＝40(人)补全条形统计图如图所示： （3）用微信人数为40人，占样本的百分比为40÷100×100%=40%，∴校共有2000名学生，估计该校最喜欢用“微信”进行沟通的学生有2000×40%＝800( 人)，答：该校有2000名学生喜欢用“微信”进行沟通的学生有800名．22．（1）证明：∵，，∴，，∴，在和中，，∴（）；（2）∵，∴，，，，∴，在和中，，∴（）；（3）∵，∴，由（2）得，，∴与的面积之和与的面积之和，故8．23．(1)①y＝−x2−2x＋3；②有最大值，有最大值时；(2)−＜m＜−1或1＜m＜(1)解：①当x＝1时，y＝0，∴m＋2m＋3＝0，∴m＝−1，∴y＝−x2−2x＋3；②l有最大值，理由如下：当x＝0时，y＝3，当y＝0时，由−x2−2x＋3＝0，∴x＝3或x＝1，∴A（−3.0）、C（0.3），∴△ACO是等腰直角三角形， 如图1，作PN⊥AB，BM⊥AB，设交于点设P（n，n2−2n＋3），∴PN＝−n2−2n＋3，HN＝AN＝3＋n，PH＝−n2−3n，BM＝AB＝4，∵PN∥BM，∴，∴l，∵−，∴当n＝−时，l有最大值，此时；(2)∵y＝mx2＋2mx＋3＝m（x＋1）2＋3−m，∴M（−1，3−m），令x＝0，则y＝3，∴C（0，3），如图2，当M点在C点下方时，过点M过MG⊥y轴交于G，∴MG＝1，CG＝3−（3−m）＝m，当α＝30°时，，∴m＝；当α＝45°时，，∴m＝1；此时1＜m＜时，如图3，当M点在C点上方时，设∠MCG＝α，CG＝3−m−3＝−m，当α＝30°时，，∴m＝−；当α＝45°时，，∴m＝−1；此时−＜m＜−1时， 综上所述：−＜m＜−1或1＜m＜， 故−＜m＜−1或1＜m＜．