2023届新疆乌鲁木齐市中考数学阶段性适应模拟试题（一模）含解析

2023届乌鲁木齐市中考数学阶段性适应模拟试题（一模）

一、单选题(每小题5分，共45分)

1．一个数在数轴上所对应的点向右移动10个单位后，得到它的相反数，则这个数是（    ）

A．5 B．–5 C．10 D．–10

2．如图所示的几何体是由两个圆柱体和一个正方体组成，圆柱体的直径和高均与正方体的棱长相等，则其俯视图是（    ）

A． B． C． D．

3．在“经典诵读”比赛活动中，某校10名学生参赛成绩如图所示，对于这10名学生的参赛成绩，下列说法错误的是（    ）

A．众数是90分 B．中位数是90分 C．平均数是91分 D．方差是1

4．全民健身活动中,组委会组织了长跑队和自行车队进行宣传,全程共10千米,自行车队的速度是长跑队速度的2.5倍,自行车队出发半小时后,长跑队才出发,结果长跑队比自行车队晚到了2小时,如果设长跑队跑步的速度为x千米/时,那么根据题意可列方程为

A．+2=+ B．-=2-0.5

C．-=2-0.5 D．-=2+0.5

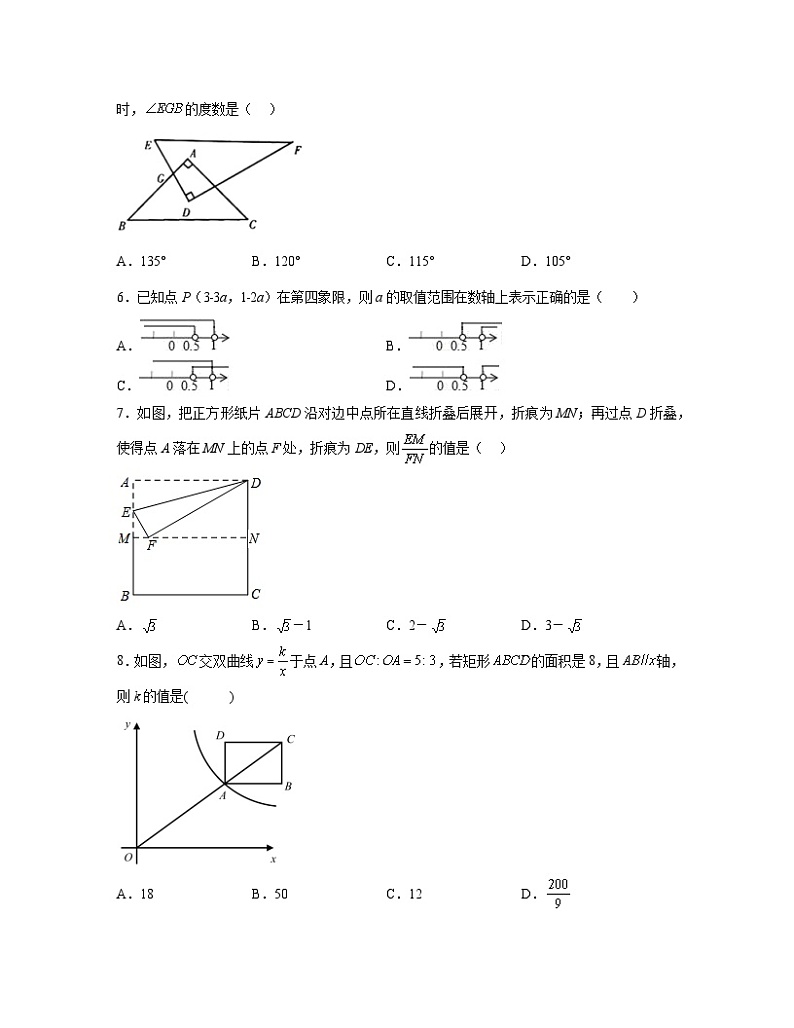
5．如图摆放的一副学生用直角三角板，，与相交于点G，当时，的度数是（    ）

A．135° B．120° C．115° D．105°

6．已知点P（3﹣3a，1﹣2a）在第四象限，则a的取值范围在数轴上表示正确的是（　　）

A． B．

C． D．

7．如图，把正方形纸片ABCD沿对边中点所在直线折叠后展开，折痕为MN；再过点D折叠， 使得点A落在MN上的点F处，折痕为DE，则的值是（    ）

A． B．－1 C．2－ D．3－

8．如图，交双曲线于点A，且，若矩形的面积是8，且轴，则k的值是(　　　)

A．18 B．50 C．12 D．

9．如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点，过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P从点A运动到点D时，点Q所经过的路径长为（　　）

A． B． C． D．π

二、填空题(每小题5分，共30分)

10．函数中，自变量的取值范围是______ ．

11．分解因式： ______ ．

12．如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分钱CF相交于F，过F作DF∥BC，交AB于D，交AC于E，若BD＝8cm，CE＝5cm，则DE的长 ___．

13．如图，四边形ABCD内接于⊙O，F是上一点，且，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC＝105°，∠BAC＝25°，则∠E的度数为______度．

14．如图，扇形AOB的圆心角是直角，半径为2，C为OB边上一点，将△AOC沿AC边折叠，圆心O恰好落在弧AB上的点D，则阴影部分面积为___________

15．如图，四边形是边长为a的正方形，点E是边上一动点（不与点B，C重合），，且EF交正方形外角的平分线于点F，交于点G，连接．有下列结论：①；②；③；④面积的最大值为．其中正确的是______．（把正确结论的序号都填上）

三、解答题(共76分)

16．（6分）计算：．

17．（7分）先化简，再求值，从，0，2，1中任选一个x的整数值代入求值．

18．（7分）如图，在ABC中，AB＝AC，AD⊥BC，垂足为D，过点A作AEBC，且AE＝BD，连接BE，交AD于点F，连接CE．

(1)求证：四边形ADCE为矩形；

(2)若CE＝4，求AF的长．

19．（9分）2021年4月15日是第七个全民国家安全教育日．为增强师生的国家安全意识，我区某中学组织了“国家安全知识竞赛”，根据学生的成绩划分为A、B、C、D四个等级，并绘制了如下不完整的条形统计图和扇形统计图：

根据图中提供的信息，回答下列问题：

(1)参加知识竞赛的学生共有 　　人；

(2)扇形统计图中，m＝　　，C等级对应的圆心角为 　　度；

(3)小永是四名获A等级的学生中的一位，学校将从获A等级的学生中任选2人，参加区举办的知识竞赛，请用列表法或画树状图，求小永被选中参加区知识竞赛的概率．

20．（10分）如图，旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处，某校数学课外兴趣小组的同学正在测量旗杆的高度，在旗杆的底部A处测得点D的仰角为15°，AC=10米，又测得∠BDA=45°．已知斜坡CD的坡度为i=1:，求旗杆AB的高度．

21．（11分）某商店准备进一批季节性小家电，每个进价为40元，经市场预测，销售定价为50元，可售出400个；定价每增加1元，销售量将减少10个，设每个定价增加x元．

（1）商店若想获得利润6000元，并且使进货量较少，则每个定价为多少元？应进货多少个？

（2）用含x的代数式表示商店获得的利润W元，并计算商店若要获得最大利润，则每个应定价多少元？获得的最大利润是多少元？

22．（12分）已知，如图，是的直径，点为上一点，于点，交于点，与交于点，点为的延长线上一点，且．

（1）求证：是的切线；

（2）求证：

（3）若，，求的长．

23．（13分）如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交AC于点D，动点P在抛物线对称轴上，动点Q在抛物线上．

（1）求抛物线的解析式；

（2）当PO+PC的值最小时，求点P的坐标；

（3）是否存在以A，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出P，Q的坐标；若不存在，请说明理由．

答案：

1．B

2．A

3．D

4．C

5．D

6．C

7．C

8．A

9．C

10．且

11．

12．3cm

13．50

14．

15．①②③

16．

17．，

18．(1)

(2)2

19．(1)40

(2)10，144

(3)

20．旗杆AB的高度约为10＋（米）．

21．（1）每个定价为70元，应进货200个；

（2）W＝﹣10（x﹣15）2+6250，每个定价为65元时获得最大利润，可获得的最大利润是6250元

22．

（2）

（3）

23．（1）y=x2+3x；

（2）当PO+PC的值最小时，点P的坐标为（2，）；

（3）存在，