

浙江省温州市新希望联盟2022-2023学年下学期八年级期中数学试卷
展开2022-2023学年浙江省温州市新希望联盟八年级(下)期中数学试卷
一、选择题(每小题3分,共30分)
1.若二次根式有意义,则x的取值范围是( )
A.x≥1 B.x≤1 C.x>1 D.x≠1
2.在下列方程中,属于一元二次方程的是( )
A. B.2(x﹣1)+x=2 C.x2=2+3x D.x2﹣xy+4=0
3.用公式法解一元二次方程3x2﹣2x﹣1=0时,计算b2﹣4ac的结果为( )
A.8 B.﹣8 C.14 D.16
4.已知甲、乙两同学1分钟跳绳的平均数相同,若甲同学1分钟跳绳成绩的方差S甲2=0.06,乙同学1分钟跳绳的方差到S乙2=0.35,则( )
A.甲的成绩比乙的成绩更稳定
B.乙的成绩比甲的成绩更稳定
C.甲、乙两人的成绩一样稳定
D.甲、乙两人的成绩稳定性不能比较
5.用配方法解方程x2﹣4x﹣3=0,则配方正确的是( )
A.(x﹣2)2=1 B.(x+2)2=1 C.(x﹣2)2=7 D.(x+2)2=7
6.下列运算正确的是( )
A. B. C. D.
7.已知a是方程x2+2x﹣1=0的一个解,则代数式﹣a2﹣2a+8的值为( )
A.0 B.5 C.6 D.7
8.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.20 B.21 C.22 D.23
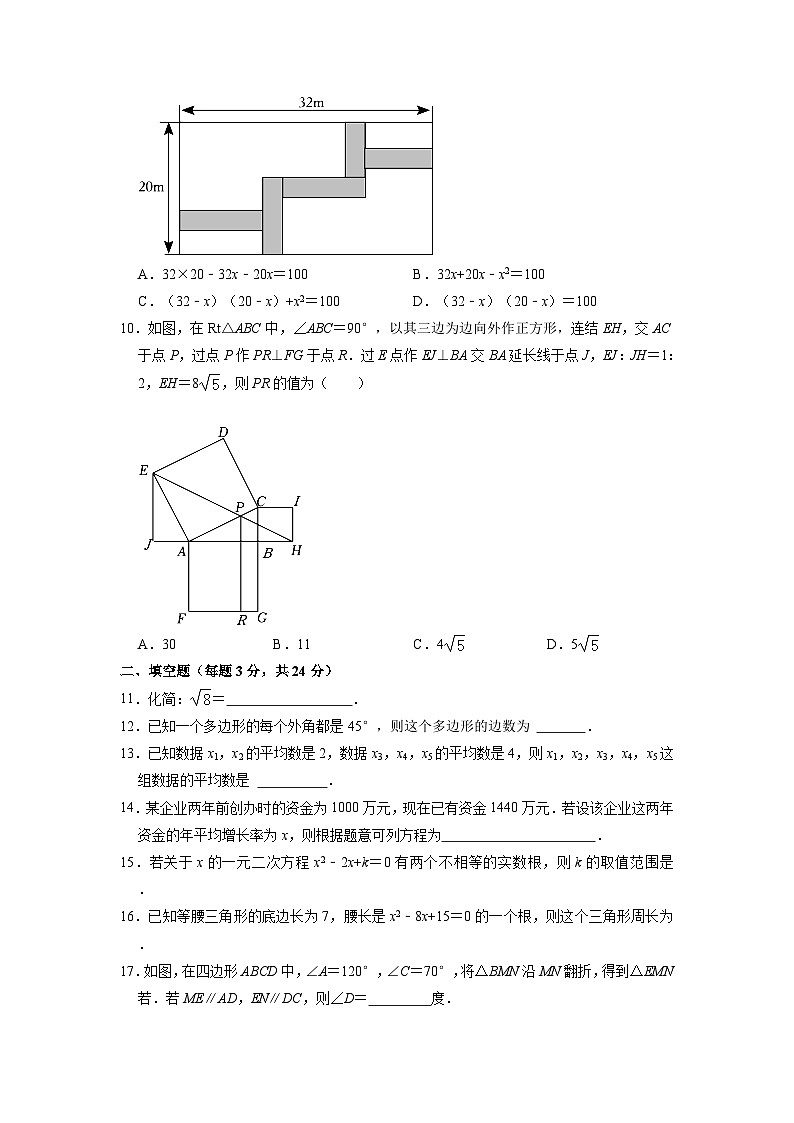
9.如图,在长为32米,宽为20米的长方形地面上修筑同样宽的小路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设小路的宽为x米,则下面所列方程正确的是( )
A.32×20﹣32x﹣20x=100 B.32x+20x﹣x2=100
C.(32﹣x)(20﹣x)+x2=100 D.(32﹣x)(20﹣x)=100
10.如图,在Rt△ABC中,∠ABC=90°,以其三边为边向外作正方形,连结EH,交AC于点P,过点P作PR⊥FG于点R.过E点作EJ⊥BA交BA延长线于点J,EJ:JH=1:2,EH=8,则PR的值为( )
A.30 B.11 C.4 D.5
二、填空题(每题3分,共24分)
11.化简:= .
12.已知一个多边形的每个外角都是45°,则这个多边形的边数为 .
13.已知数据x1,x2的平均数是2,数据x3,x4,x5的平均数是4,则x1,x2,x3,x4,x5这组数据的平均数是 .
14.某企业两年前创办时的资金为1000万元,现在已有资金1440万元.若设该企业这两年资金的年平均增长率为x,则根据题意可列方程为 .
15.若关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是 .
16.已知等腰三角形的底边长为7,腰长是x2﹣8x+15=0的一个根,则这个三角形周长为 .
17.如图,在四边形ABCD中,∠A=120°,∠C=70°,将△BMN沿MN翻折,得到△EMN若.若ME∥AD,EN∥DC,则∠D= 度.
18.如图,O是平面直角坐标系原点,AB∥OC,AO⊥OC,AB=1,OC=4,P为线段AO上一个动点,连结PB并延长至点E,使得点E落在直线x=2上,以PE,PC为邻边作▱PEFC,则对角线PF的最小值为 .
三、解答题(共46分)
19.计算:.
20.解方程:x2+6x﹣7=0.
21.某工艺品厂草编车间共有16名工人,调查每个工人的日均生产能力,获得数据如下表:
日均生产能力(件)
10
11
12
13
14
16
人数
1
2
6
4
2
1
(1)这16名工人日均生产件数的平均数= 件,众数= 件,中位数= 件;
(2)为了提高工作效率和工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,应选择什么统计量作为日生产件数的定额?
22.如图①、图②均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B均在格点上.只用无刻度的直尺,在给定的网格中按下列要求作图,所作图形的顶点均在格点上且两图形不全等,不要求写作法.
(1)在图①中以线段AB为边作一个平行四边形;
(2)在图②中以线段AB为边作一个平行四边形,且有一条对角线长为2.
23.根据以下信息,探索完成任务.
如何设计种植方案?
素材1
小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践,现有A、B两种作物的相关信息如下表所示:
A作物
B作物
每平方米种植株树(株)
2
10
单株产量(千克)
1.2
0.5
素材2
由于A作物植株间距较大,可增加A作物每平方米的种植株树.经过调研发现,每平方米种植A作物每增加1株,A作物的单株产量减少0.1千克.
素材3
若同时种植A、B两种作物,实行分区域种植.
问题解决
单一种植(全部种植A作物)
任务1:明确数量关系
设每平方米增加x株A作物(x为正整数),则每平方米有 株,单株产量为
千克. (用含x的代数式表示)
任务2:计算产量
要使A作物每平方米产量为4.8千克,则每平方米应种植多少株?
分区种植(种植A、B两种作物)
任务3:规划种植方案
设这100平方米的土地中有a平方米用于种植A作物,且每平方米产量最大,其余区域按照每平方米10株种植B作物,当这100平方米总产量不低于496千克时,则a的取值范围是 .
24.如图,在平面直角坐标系中,以B为原点,C(6,0),A(0,8),有一动点P以每秒3个单位的速度从点C出发向终点B运动,同时还有一动点Q以每秒5个单位的速度也从点C出发,向终点A运动,连结PQ,且PQ⊥BC,以CP,CQ为邻边作▱CQMP,设动点P的运动时间为t秒.
(1)BP= ;(用含t的代数式表示)
(2)连结BM,当△BPM为等腰三角形时,求t的值;
(3)若以直线AM为对称轴,当点Q的对称点恰好落在y轴上时,则t的值为 .( 直接写出答案)
参考答案
一、选择题(每小题3分,共30分)
1.若二次根式有意义,则x的取值范围是( )
A.x≥1 B.x≤1 C.x>1 D.x≠1
【分析】根据二次根式有意义的条件可得x﹣1≥0,再解不等式即可.
解:由题意得:x﹣1≥0,
解得:x≥1,
故选:A.
【点评】此题主要考查了二次根式有意义的条件,二次根式的被开方数是非负数.
2.在下列方程中,属于一元二次方程的是( )
A. B.2(x﹣1)+x=2 C.x2=2+3x D.x2﹣xy+4=0
【分析】根据一元二次方程的定义对各选项进行判断.
解:A.方程x2+3x=为分式方程,所以A选项不符合题意;
B.方程2(x﹣1)+x=2为一元一次方程,所以B选项不符合题意;
C.方程x2=2+3x为一元二次方程,所以C选项符合题意;
D.方程x2﹣xy+4=0为二元二次方程,所以D选项不符合题意.
故选:C.
【点评】本题考查了一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程.
3.用公式法解一元二次方程3x2﹣2x﹣1=0时,计算b2﹣4ac的结果为( )
A.8 B.﹣8 C.14 D.16
【分析】根据方程的系数可得出a,b,c的值,再将其代入b2﹣4ac中即可求出结论.
解:∵a=3,b=﹣2,c=﹣1,
∴Δ=b2﹣4ac=(﹣2)2﹣4×3×(﹣1)=16.
故选:D.
【点评】本题考查了根的判别式,牢记根的判别式Δ=b2﹣4ac是解题的关键.
4.已知甲、乙两同学1分钟跳绳的平均数相同,若甲同学1分钟跳绳成绩的方差S甲2=0.06,乙同学1分钟跳绳的方差到S乙2=0.35,则( )
A.甲的成绩比乙的成绩更稳定
B.乙的成绩比甲的成绩更稳定
C.甲、乙两人的成绩一样稳定
D.甲、乙两人的成绩稳定性不能比较
【分析】方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
解:∵甲、乙两同学1分钟跳绳的平均数相同,若甲同学1分钟跳绳成绩的方差S甲2=0.06,乙同学1分钟跳绳成绩的方差S乙2=0.35,
∴S甲2<S乙2,
∴甲的成绩比乙的成绩更稳定.
故选:A.
【点评】本题考查了方差、算术平均数等知识,掌握方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好是关键.
5.用配方法解方程x2﹣4x﹣3=0,则配方正确的是( )
A.(x﹣2)2=1 B.(x+2)2=1 C.(x﹣2)2=7 D.(x+2)2=7
【分析】先把﹣3移到方程的右边,然后方程两边都加4,再把左边根据完全平方公式写成完全平方的形式即可.
解:∵x2﹣4x﹣3=0,
∴x2﹣4x=3,
∴x2﹣4x+4=3+4,
∴(x﹣2)2=7.
故选:C.
【点评】本题考查了解一元二次方程﹣配方法:将一元二次方程配成(x+m)2=n(n≥0)的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.
6.下列运算正确的是( )
A. B. C. D.
【分析】根据二次根式的加减法对A、D进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的除法法则对C进行判断.
解:A、与不能合并,所以A选项错误;
B、原式=6×2=12,所以B选项错误;
C、原式==2,所以C选项准确;
D、原式=2,所以D选项错误.
故选:C.
【点评】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
7.已知a是方程x2+2x﹣1=0的一个解,则代数式﹣a2﹣2a+8的值为( )
A.0 B.5 C.6 D.7
【分析】根据一元二次方程的解的定义,将x=a代入已知方程,即可求得a2﹣2a=1,然后将其代入所求的代数式并求值即可.
解:∵a是方程x2+2x﹣1=0的一个解,
∴a2+2a=1,
则﹣a2﹣2a+8=﹣(a2+2a)+8=﹣1+8=7.
故选:D.
【点评】本题考查的是一元二次方程的根即方程的解的定义.方程的根即方程的解,就是能使方程左右两边相等的未知数的值.
8.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.20 B.21 C.22 D.23
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选:A.
【点评】此题考查了平行四边形的性质以及勾股定理.注意掌握平行四边形的对角线互相平分.
9.如图,在长为32米,宽为20米的长方形地面上修筑同样宽的小路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设小路的宽为x米,则下面所列方程正确的是( )
A.32×20﹣32x﹣20x=100 B.32x+20x﹣x2=100
C.(32﹣x)(20﹣x)+x2=100 D.(32﹣x)(20﹣x)=100
【分析】设道路的宽x米,小路的面积+x2=一个长32宽x的矩形面积+一个长20宽x的矩形的面积,即可得出关于x的一元二次方程,此题得解.
解:设道路的宽x米,
则32x+20x=100+x2.
32x+20x﹣x2=100.
故选:B.
【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
10.如图,在Rt△ABC中,∠ABC=90°,以其三边为边向外作正方形,连结EH,交AC于点P,过点P作PR⊥FG于点R.过E点作EJ⊥BA交BA延长线于点J,EJ:JH=1:2,EH=8,则PR的值为( )
A.30 B.11 C.4 D.5
【分析】设PR与AB交于点N,利用正方形性质可证得△ACB≌△EAJ(AAS),得出EJ=AB,AM=BC,设AB=x,BC=y,根据tan∠AHE==,可得EJ=2y,JH=4y,利用勾股定理建立方程求解可得x=8,再由tan∠CAB=,可得PA=PH,利用等腰三角形性质和解直角三角形可求得PH=3,再证明四边形BGRN是矩形,得出NR=BG=8,利用PR=PN+NR即可求得答案.
解:设PR与AB交于点N,
∵四边形ACDE、BCIH、ABGF均为正方形,
∴AE=AC,BC=BH,AB=BG,∠CAE=∠CBH=∠ABG=∠G=90°,AB∥FG,
∵∠ABC=90°,
∴∠ABC=∠M=90°,
∴∠ACB+∠CAB=90°,
∵∠EAJ+∠CAB=90°,
∴∠ACB=∠EAJ,
∴△ACB≌△EAJ(AAS),
∴EJ=AB,AJ=BC,
∴AJ=BH=BC,
设AB=x,BC=y,
则EJ=x,AJ=BH=y,
JH=x+2y,
∵tan∠AHE=,
∴,即JH=2EJ,
∴x+2y=2x,
∴x=2y,
∴EJ=2y,JH=4y,
∵EJ2+JH2=EH2,
∴(2y)2+(4y)2=(8)2,
解得:y=4或y=﹣4(舍去),
∴x=8,
∴AJ=BC=BH=4,AB=BG=8,
∵∠ABC+∠CBH=180°,
∴A、B、H三点共线,
∴AH=AB+BH=8+4=12,
∵tan∠CAB=,
∴tan∠CAB=tan∠AHE,
∴∠CAB=∠AHE,
∴PA=PH,
∵AB∥FG,
∴∠PNB=∠PRG=90°,
∴AN=AH=×12=6,
∴=tan∠CAB=,
∴PN=AN=×6=3,
∵PR⊥FG,
∴∠PRG=90°,
∴∠ABC=∠G=∠PRG=90°,
∴四边形BGRN是矩形,
∴NR=BG=8,
∴PR=PN+NR=3+8=11.
故选:B.
【点评】本题主要考查了勾股定理,正方形的性质,全等三角形的判定与性质,矩形的判定与性质,勾股定理,三角函数定义等知识,利用勾股定理建立方程求得AB=8,BC=4是解题的关键.
二、填空题(每题3分,共24分)
11.化简:= 2 .
【分析】应用二次根式的化简的方法进行计算即可得出答案.
解:===2.
故答案为:2.
【点评】本题主要考查了二次根式的化简,熟练掌握二次根式的化简的计算方法进行求解是解决本题的关键.
12.已知一个多边形的每个外角都是45°,则这个多边形的边数为 八 .
【分析】根据多边形的外角和是360°求解即可.
解:∵360÷45=8(边),
∴多边形的边数为八,
故答案为:八.
【点评】本题考查了多边形的内角与外角,掌握多边形的外角和是360°是解题的关键.
13.已知数据x1,x2的平均数是2,数据x3,x4,x5的平均数是4,则x1,x2,x3,x4,x5这组数据的平均数是 3.2 .
【分析】根据加权平均数的定义分别求出两组数的和,再按照加权平均数的计算方法计算即可解答.
解:∵数据x1,x2,x3的平均数是2,
数据x4,x5的平均数是4,
∴数据x1,x2,x3,x4,x5的平均数是=3.2.
故答案为:3.2.
【点评】本题考查的是加权平均数的求法.求出5个数的总和,掌握加权平均数的求法是解答本题的关键.
14.某企业两年前创办时的资金为1000万元,现在已有资金1440万元.若设该企业这两年资金的年平均增长率为x,则根据题意可列方程为 1000(1+x)2=1440 .
【分析】根据关系式:现在已有资金1000万元×(1+年平均增长率)2=现在已有资金1440万元,把相关数值代入即可求解.
解:设该企业这两年资金的年平均增长率为x,根据题意得:
1000(1+x)2=1440.
故答案为1000(1+x)2=1440.
【点评】此题主要考查了由实际问题抽象出一元二次方程,关键是掌握增长率问题的计算公式:变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.
15.若关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是 k<1 .
【分析】根据根的判别式的意义得到(﹣2)2﹣4k>0,然后解不等式即可.
解:根据题意得Δ=(﹣2)2﹣4×k>0,
解得k<1.
故答案为:k<1.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系,当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.上面的结论反过来也成立.
16.已知等腰三角形的底边长为7,腰长是x2﹣8x+15=0的一个根,则这个三角形周长为 17 .
【分析】求出方程的解,得出两组情况,看看是否符合三角形三边关系定理,求出即可.
解:x2﹣8x+15=0,
(x﹣5)(x﹣3)=0,
x﹣5=0,x﹣3=0,
x1=5,x2=3,
即①等腰三角形的三边为7,5,5,此时符合三角形三边关系定理,三角形的周长是5+5+7=17;
②等腰三角形的三边为3,3,7,此时不符合三角形三边关系定理,
故答案为:17.
【点评】本题考查了解一元二次方程和三角形三边关系定理,等腰三角形性质的应用,关键是确定三角形的三边长.
17.如图,在四边形ABCD中,∠A=120°,∠C=70°,将△BMN沿MN翻折,得到△EMN若.若ME∥AD,EN∥DC,则∠D= 70 度.
【分析】由平行线的性质得出∠BME=120°,∠ENB=70°,再由翻折变换的性质得出∠EMN=∠BMN=60°,∠ENM=∠MNB=35°,进而求出∠B的度数,即可得出∠D的度数.
解:∵ME∥AD,EN∥DC,∠A=120°,∠C=70°,
∴∠BME=∠A=120°,∠ENB=∠C=70°,
∵将△BMN沿MN翻折得△EMN,
∴∠EMN=∠BMN=60°,∠ENM=∠MNB=35°,∠E=∠B,
∴∠E=∠B=180°﹣60°﹣35°=85°,
∴∠D=360°﹣120°﹣70°﹣85°=85°,
故答案为:70.
【点评】此题主要考查了翻折变换的性质、平行线的性质、三角形内角和定理以及多边形内角和定理等知识,熟练掌握翻折变换的性质是解题关键.
18.如图,O是平面直角坐标系原点,AB∥OC,AO⊥OC,AB=1,OC=4,P为线段AO上一个动点,连结PB并延长至点E,使得点E落在直线x=2上,以PE,PC为邻边作▱PEFC,则对角线PF的最小值为 6 .
【分析】作FN⊥x轴于N,EM⊥y轴于M,连接PF.利用全等三角形的性质证明CN=EM=2,推出ON=6,根据垂线段最短解决问题即可.
解:作FN⊥x轴于N,EM⊥y轴于M,连接PF.
∵四边形PEFC是平行四边形,
∴PE=CF,PE∥CF,
∴∠FCN=∠ETC,
∵EM⊥y轴,FN⊥x轴,
∴∠EMP=∠FNC=90°,
∵EM∥TC,
∴∠MEP=∠ETC,
∴∠MEP=∠FCN,
∴△EMA≌△CNF(AAS),
∴EM=CN=2,
∵OC=4,
∴ON=OC+CN=4+2=6,
当PF⊥FN时,PF的值最小,此时PF=ON=6,
∴PF的最小值为6.
故答案为6.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用垂线段最短解决最短问题.
三、解答题(共46分)
19.计算:.
【分析】先根据二次根式的乘法和除法法则运算,然后化简二次根式后合并即可.
解:原式=4﹣+2
=4﹣+2
=5.
【点评】本题考查了二次根式的混合运算,熟练掌握二次根式的性质、二次根式的乘法和除法法则是解决问题的关键.
20.解方程:x2+6x﹣7=0.
【分析】首先把一元二次方程x2+6x﹣7=0转化成两个一元一次方程的乘积,即(x+7)(x﹣1)=0,然后解一元一次方程即可.
解:∵x2+6x﹣7=0,
∴(x+7)(x﹣1)=0,
∴x1=﹣7或x2=1.
【点评】本题主要考查了因式分解法解一元二次方程的知识,解答本题的关键是掌握因式分解法解一元二次方程的步骤,此题难度不大.
21.某工艺品厂草编车间共有16名工人,调查每个工人的日均生产能力,获得数据如下表:
日均生产能力(件)
10
11
12
13
14
16
人数
1
2
6
4
2
1
(1)这16名工人日均生产件数的平均数= 12.5 件,众数= 12 件,中位数= 12 件;
(2)为了提高工作效率和工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,应选择什么统计量作为日生产件数的定额?
【分析】(1)平均数=加工零件总数÷总人数,中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,如果数据的个数是偶数就是中间两个数的平均数,众数是指一组数据中出现次数最多的数据;
(2)分别从平均数、中位数和众数的角度,讨论达标人数和获奖人数情况,从而得出结论.
解:(1)由表格可得,
平均数为:×(10+11×2+12×6+13×4+14×2+16)=12.5(件),
12出现的次数最多,故众数是12,
16名工人日均生产件数从小到大排列,排在中间的数分别为12、12,故中位数是=12(件);
故答案为:12.5,12,12;
(2)当定额为13个时,有13人达标,3人获奖,不利于提高工人的积极性,
当定额为12个时,有9人达标,7人获奖,利于提高大多数工人的积极性,
∴定额为12个时,有利于提高大多数工人的积极性,
故应选择中位数作为日生产件数的定额.
【点评】本题考查了统计量的选择,平均数、众数、中位数的意义,掌握平均数、众数、中位数的定义是关键.
22.如图①、图②均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B均在格点上.只用无刻度的直尺,在给定的网格中按下列要求作图,所作图形的顶点均在格点上且两图形不全等,不要求写作法.
(1)在图①中以线段AB为边作一个平行四边形;
(2)在图②中以线段AB为边作一个平行四边形,且有一条对角线长为2.
【分析】(1)根据平行四边形的定义画出图形即可(答案不唯一);
(2)根据要求画出图形(答案不唯一).
解:(1)如图①中,平行四边形ABCD即为所求;
(2)如图②中,平行四边形ABCD即为所求.
【点评】本题考查作图﹣全等图形,勾股定理,平行四边形的判定和性质等知识,解题的关键是掌握平行四边形的判定和性质,属于中考常考题型.
23.根据以下信息,探索完成任务.
如何设计种植方案?
素材1
小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践,现有A、B两种作物的相关信息如下表所示:
A作物
B作物
每平方米种植株树(株)
2
10
单株产量(千克)
1.2
0.5
素材2
由于A作物植株间距较大,可增加A作物每平方米的种植株树.经过调研发现,每平方米种植A作物每增加1株,A作物的单株产量减少0.1千克.
素材3
若同时种植A、B两种作物,实行分区域种植.
问题解决
单一种植(全部种植A作物)
任务1:明确数量关系
设每平方米增加x株A作物(x为正整数),则每平方米有 (2+x) 株,单株产量为
(1.2﹣0.1x) 千克. (用含x的代数式表示)
任务2:计算产量
要使A作物每平方米产量为4.8千克,则每平方米应种植多少株?
分区种植(种植A、B两种作物)
任务3:规划种植方案
设这100平方米的土地中有a平方米用于种植A作物,且每平方米产量最大,其余区域按照每平方米10株种植B作物,当这100平方米总产量不低于496千克时,则a的取值范围是 a≤4 .
【分析】任务一:根据题意直接得出结论;
任务二:根据单株产量×每平米的株数=4.8列出方程,解方程即可;
任务三:现根据种植A作物每平米的产量=单株产量×每平米的株数列出函数解析式,根据函数的性质求出种植A作物每平米的最高产量,再根据100平米种植A作物和B作物的产量之和≥496列出不等式,解不等式即可.
解:任务一:设每平方米增加x株A作物(x为正整数),则每平方米有(2+x)株,单株产量为(1.2﹣0.1x)千克,
故答案为:(2+x),(1.2﹣0.1x);
任务二:根据题意得:(2+x)(1.2﹣0.1x)=4.8,
整理得:x2﹣10x+24=0,
解得:x1=4,x2=6,
∴x+4=6或x+2=8,
答:每平方米应种植6株或8株;
任务三:设种植A作物每平方米的产量为y千克,
根据题意得:y=(2+x)(1.2﹣0.1x)=﹣0.1x2+x+2.4=﹣0.1(x﹣5)2+4.9,
∵﹣0.1<0,
∴当x=5时,y有最大值,最大值为4.9,
∴种植A作物每平方米最大产量为1.9千克,
根据题意得:4.9a+(100﹣a)×10×0.5≥496,
解得a≤40,
则a的取值范围是a≤40,
故答案为:a≤40.
【点评】本题考查二次函数和一元二次方程的应用,关键是找到等量关系列出函数解析式和一元二次方程.
24.如图,在平面直角坐标系中,以B为原点,C(6,0),A(0,8),有一动点P以每秒3个单位的速度从点C出发向终点B运动,同时还有一动点Q以每秒5个单位的速度也从点C出发,向终点A运动,连结PQ,且PQ⊥BC,以CP,CQ为邻边作▱CQMP,设动点P的运动时间为t秒.
(1)BP= 6﹣3t ;(用含t的代数式表示)
(2)连结BM,当△BPM为等腰三角形时,求t的值;
(3)若以直线AM为对称轴,当点Q的对称点恰好落在y轴上时,则t的值为 .( 直接写出答案)
【分析】(1)根据题意有BP=BC﹣CP,进而得可得答案;
(2)分三种情况,利用等腰三角形,勾股定理列方程解答即可;
(3)设Q关于AM的对称点为Q',过M作MR⊥BC于R,延长QM交AB于K,可得CQ=5t,PR=MQ=CP=3t,PQ=4t=MR,由MQ∥CP,CP⊥AB,知∠QKQ'=90°,四边形KBRM是矩形,在Rt△KMQ'中可得KQ'==,而AQ=AC﹣CQ=10﹣5t,即得8﹣4t+=10﹣5t,解方程可得答案.
解:(1)设点P的运动时间为t秒,则CP=3t,
∵C(6,0),
∴BC=6,
∴BP=BC﹣PC=6﹣3t,
故答案为:6﹣3t;
(2)设点P的运动时间为t秒,则CP=3t,CQ=5t,
∵四边形CQMP是平行四边形,
∴MP=CQ=5t,
①当BP=PM时,如图:
∴6﹣3t=5t,
解得:t=;
②当BM=PM时,过M作MH⊥BC于H,如图:
∵PQ⊥BC,MH⊥BC,
∴MH∥PQ,
∵四边形CQMP是平行四边形,
∴MQ∥CP,MQ=CP,
∴四边形MHPQ是矩形,
∴HP=MQ=CP,
∵BM=PM,MH⊥BC,
∴BH=HP,
∴BH=HP=CP,
∴CP=BC=×6=2,
∴t==;
③当BM=BP时,过M作MG⊥BC于G,如图:
∵PQ⊥BC,CP=3t,CQ=5t,
∴PQ=4t,
同②可得GP=MQ=CP=3t,MG=PQ=4t,
∴BG=BC﹣GP﹣CP=6﹣6t,BM=BP=BC﹣CP=6﹣3t,
在Rt△BGM中,BG2+MG2=BM2,
∴(6﹣6t)2+(4t)2=(6﹣3t)2,
解得t=0(舍去)或t=;
综上所述,当△BPM为等腰三角形时,t的值为或或;
(3)设Q关于AM的对称点为Q',过M作MR⊥BC于R,延长QM交AB于K,如图:
同(2)可得CQ=5t,PR=MQ=CP=3t,PQ=4t=MR,
∵MQ∥CP,CP⊥AB,
∴MQ⊥AB,即∠QKQ'=90°,
∵∠KBR=90°=∠BRM,
∴四边形KBRM是矩形,
∴KB=MR=PQ=4t,KM=BR=BC﹣PR﹣CP=6﹣6t,
∴AK=AB﹣KB=8﹣4t,
∵点Q的对称点为Q',
∴MQ'=MQ=3t,
在Rt△KMQ'中,
KQ'==,
∴AQ'=AK+KQ'=8﹣4t+,
∵AB=8,BC=6,
∴AC=10,
∴AQ=AC﹣CQ=10﹣5t,
∵AQ'=AQ,
∴8﹣4t+=10﹣5t,
解得t=2(不符合题意,舍去)或t=,
∴t的值为;
故答案为:.
【点评】本题考查四边形综合应用,涉及等腰三角形性质及应用,平行四边形性质及应用,矩形的判定与性质,勾股定理及应用等知识,解题的关键是分类讨论思想的应用.
2023-2024学年浙江省温州市新希望联盟校七年级(上)期中数学试卷(含解析): 这是一份2023-2024学年浙江省温州市新希望联盟校七年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年浙江省温州市新希望联盟七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年浙江省温州市新希望联盟七年级(下)期中数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年浙江省温州市新希望联盟八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年浙江省温州市新希望联盟八年级(下)期中数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












