衡水中学新高二开学检测卷数学试题03

这是一份衡水中学新高二开学检测卷数学试题03，共19页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。
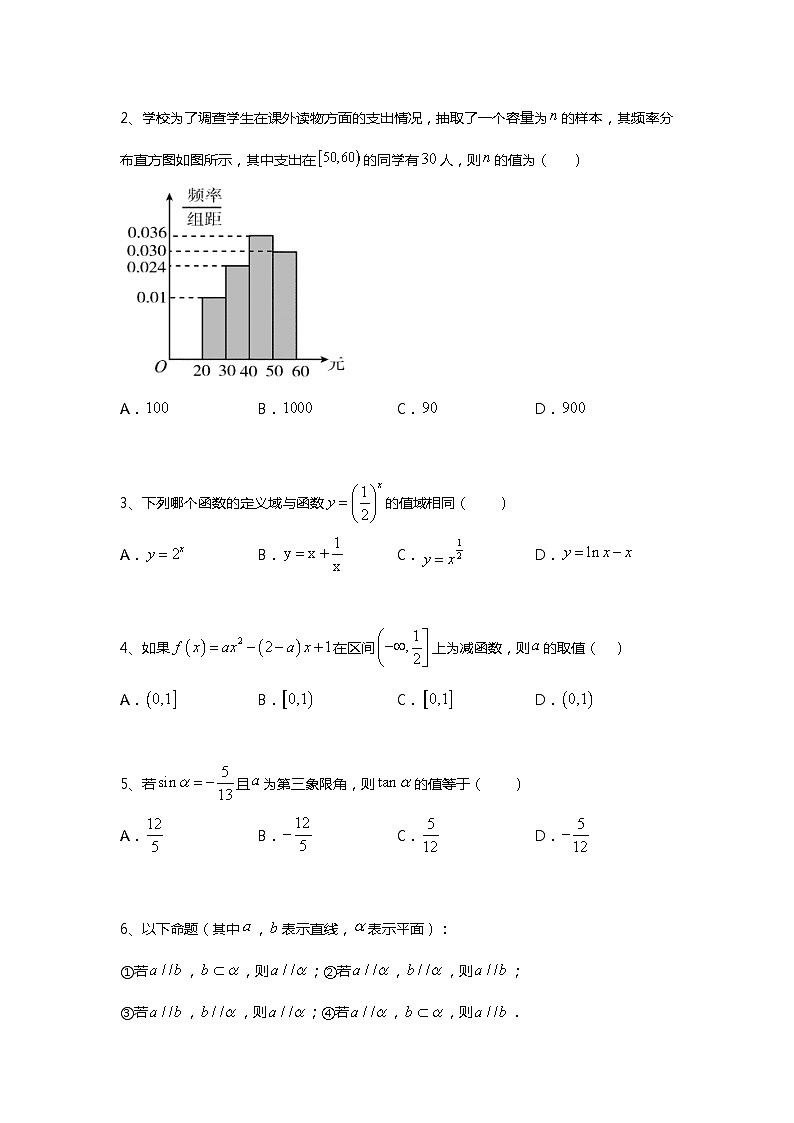
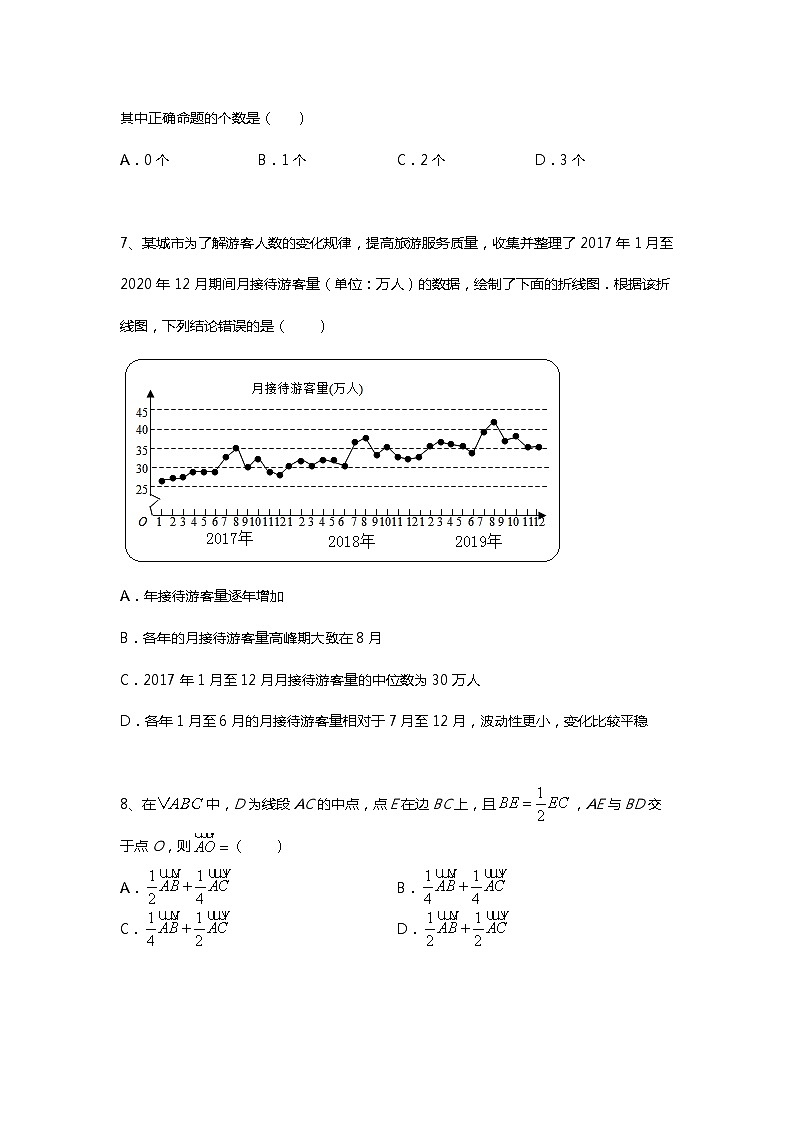
2020年衡水中学新高二开学检测卷 数学试题 本试卷共22题，满分150分。考试结束后，将本试卷和答题卡一并交回。 注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。 2．答题时请按要求用笔。  3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。 4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。 5．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。  一、单选题（共8小题，满分40分，每小题5分）1、设全集为R，集合A＝{x|0＜x＜2}，B＝{x|x≥1}，则A∩B＝（　　　　）A．{x|1≤x＜2} B．{x|0＜x＜2} C．{x|0＜x≤1} D．{x|0＜x＜1} 2、学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为的样本，其频率分布直方图如图所示，其中支出在的同学有人，则的值为（   ）A． B． C． D． 3、下列哪个函数的定义域与函数的值域相同（    ）A． B． C． D． 4、如果在区间上为减函数，则的取值（  ）A． B． C． D． 5、若且为第三象限角，则的值等于（    ）A． B． C． D． 6、以下命题（其中，表示直线，表示平面）：①若，，则；②若，，则；③若，，则；④若，，则．其中正确命题的个数是（   ）A．0个 B．1个 C．2个 D．3个 7、某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2017年1月至2020年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（　　）A．年接待游客量逐年增加B．各年的月接待游客量高峰期大致在8月C．2017年1月至12月月接待游客量的中位数为30万人D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳 8、在中，D为线段AC的中点，点E在边BC上，且，AE与BD交于点O，则（    ）A． B．C． D． 二、多选题（共4小题，满分20分，每小题5分，少选的3分，多选不得分）9、下列关系中，正确的有（）A． B． C． D． 10、在中,下列关系恒成立的是（    ）A． B．C． D． 11、某市12月17日至21日期间空气质量呈现重度及以上污染水平,经市政府批准,该市启动了空气重污染红色预警,期间实行机动车“单双号”限行等措施.某报社会调查中心联合问卷网,对2400人进行问卷调查,并根据调查结果得到如下饼图则下列结论正确的是（    ）A．“不支持”部分所占的比例大约是整体的;B．“一般”部分所占的人数估计是800人;C．饼图中如果圆的半径为2,则“非常支持”部分扇形的面积是;D．“支持”部分所占的人数估计是1100人 12、以下四个命题表述正确的是（    ）A．直线恒过定点B．圆上有且仅有3个点到直线的距离都等于1C．曲线与曲线恰有三条公切线，则D．已知圆，点为直线上一动点，过点向圆引两条切线、，、为切点，则直线经过定点 三、填空题（共4小题，满分20分，每小题5分，一题两空，第一空2分）13、函数 的定义域为_____. 14、已知函数的值域为，则实数的取值范围是_____. 15、已知函数.在处取得最大值，则________；若函数的周期是，函数的单调增区间是________. 16、在平面直角坐标系中，是圆的弦，且，若存在线段的中点，使得点关于轴对称的点在直线上，则实数的取值范围是_______________________. 四、解答题（共6小题，满分70分，第17题10分，其它12分）17、在平面直角坐标系中，已知，.（Ⅰ）若，求实数的值；（Ⅱ）若，求实数的值. 18、某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成，，，，，六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题：（1）求分数内的频率，并补全这个频率分布直方图；（2）从频率分布直方图中，估计本次考试成绩的中位数；（3）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率. 19、如图四棱锥中，底面是边长为的正方形，其它四个侧面是侧棱长为的等腰三角形，为的中点，为的中点.（1）证明：平面；（2）求三棱锥的体积 20、在中，边上的高所在直线的方程为，的平分线所在直线方程为，若点的坐标为．（1）求点和点的坐标；（2）求边上的高所在的直线的方程． 21、已知函数．求的对称轴所在直线方程及其对称中心；在中，内角A、B、C所对的边分别是a、b、c，且，，求周长的取值范围． 22、已知函数，分别是定义在上的偶函数和奇函数，且．（1）求函数，的解析式；（2）若对任意，不等式恒成立，求实数的最大值；（3）设，若函数与的图象有且只有一个公共点，求的取值范围．
参考答案 1.【答案】A【解析】由集合，，所以.故选：A. 2.【答案】A【解析】由频率分布直方图可知，支出在的同学的频率为：，本题正确选项： 3.【答案】D【解析】指数函数的值域是A选项定义域是R；B选项定义域是；C选项定义域是；D选项定义域是，满足题意。故选：D 4.【答案】C【解析】由题意，当时，可得，在上是单调递减，满足题意，当时，显然不成立；当时，要使在上为减函数，则，解得：.综上：可得，故选：. 5.【答案】C【解析】因为且为第三象限角，所以，则.故选：C 6.【答案】A【解析】①若a∥b，b⊂α，则a∥α或a⊂α，故错；②若a∥α，b∥α，则a，b平行、相交或异面，故②错；③若a∥b，b∥α，则a∥α或a⊂α，故③错；④若a∥α，b⊂α，则a、b平行或异面，故④错．正确命题个数为0个，故选：A. 7.【答案】C【解析】由2017年1月至2020年12月期间月接待游客量的折线图得：在中，年接待游客量虽然逐月波动，但总体上逐年增加，故正确；在中，各年的月接待游客量高峰期都在8月，故正确；在中，2017年1月至12月月接待游客量的中位数小于30万人，故错误；在中，各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳，故正确．故选：． 8.【答案】A【解析】根据题意, 在中,D为线段AC的中点,点E在边BC上,且,AE与BD交于点,如下图所示:因为共线, 共线可设则同时由上述两式可得,解得所以代入，故选:A 9.【答案】AB【解析】选项A:由空集是任何非空集合的真子集可知，本选项是正确的；选项B: 是有理数，故是正确的；选项C:所有的整数都是有理数，故有，所以本选项是不正确的；选项D; 由空集是任何集合的子集可知，本选项是不正确的，故本题选AB. 10.【答案】BD【解析】A选项：，不正确；B选项：,正确；C选项： ,不正确；D选项：,正确.故选：BD 11.【答案】ACD【解析】A选项：“不支持”部分所占，所以比例大约是整体的，正确。B选项：“一般”部分所占比例为，所以占的人数估计是人，不正确；C选项：“非常支持”部分占比例，所以面积是，正确； D选项：“支持”部分所占比例，共有，正确.故选：ACD 12.【答案】BCD【解析】A.直线得，
由，得，即直线恒过定点，故A错误；B. 圆心到直线的距离，圆的半径，故圆C上有3个点到直线的距离为1，故B正确；C. 曲线，即，曲线，即，两圆心的距离为，解得，故C正确；D. 因为点为直线上一动点，设点，圆的圆心为，以线段为直径的圆的方程为，即故直线圆与圆的公共弦方程为：，即，此直线即为直线，经验证点在直线上，即直线经过定点，故D正确.故选：BCD. 13.【答案】【解析】由题意可知，，解得，所以的定义域为.故答案为：. 14.【答案】【解析】当时,,此时值域为若值域为,则当时.为单调递增函数,且最大值需大于等于1，即,解得，故答案为: 15.【答案】    ，    【解析】由在处取得最大值,得,,,,,.函数的周期是,所以,,,的周期为,由,,函数的单调增区间是,.故答案为：（1）;（2）,. 16.【答案】【解析】因为点为弦的中点,所以,在中,,,所以,所以点的轨迹为以为圆心,为半径的圆,因为点与点关于轴对称,所以点的轨迹为以为圆心,为半径的圆,因为点在直线上,所以直线与圆:有交点,所以,即,解得,故答案为:  17.【答案】（Ⅰ）；（Ⅱ）.【解析】（Ⅰ），，，，，，解得；（Ⅱ），，，解得. 18.【答案】(1)见解析(2) (3) 【解析】（1）设分数在内的频率为，根据频率分布直方图，则有，可得，所以频率分布直方图为：（2）以中位数为准做一条垂直于横轴的直线，这条直线把频率分布直方图分成面积相等的两个部分，由频率分布直方图知中位数要把最高的小长方形三等分，所以中位数是，所以估计本次考试成绩的中位数为（3）设所抽取2人成绩之差的绝对值大于10为事件，第1组学生数：人（设为1，2，3，4，5，6）第6组学生数：人（设为）所有基本事件有：12，13，14，15，16，，23，24，25，26，，，，34，35，36，，，，45，46，，,，56，，，，，，，，，共有35种，事件包括的基本事件有：，，，，，，，，,，，，，，，共有18种所以.     19.【答案】（1）见解析；（2）【解析】（1）∵取的中点为，连、，∵为的中点，∴．∵为正方形，为的中点，∴，∴．∴四边形是，∴．又 ∵，故平面．（2）∵为的中点，，∴，∵为正四棱锥，∴在平面的射影为的中点，∵，，∴，∴，∴． 20.【答案】（1）（2）【解析】（1）由已知点应在边上的高所在直线与的角平分线所在直线的交点，由得，故．由，所以所在直线方程为，所在直线的方程为，由，得．（2）由（1）知，所在直线方程，所以所在的直线方程为，即． 21.【答案】（1）对称轴方程为，，对称中心为，（2）【解析】（1）由，∴∴的对称轴方程为，由，∴，∴的对称中心为，（2）∵，∴，∴，∴，得：，，∴又，∴，∴ 22.【答案】（1），；（2）4；（3）或【解析】（1），用代替得，则，解方程得：，.（2）对任意恒成立，令，，因为令在单调递增，故则对恒成立当时， 故，即（3）由题：方程有且只有一个根即有且只有一个根，令，因为在上单调递增，且故方程（*式）有且只有一个正根①当时，方程有唯一根，合题②当时，方程变形为，解得两根为，因为（*式）有且只有一个正根，故或，解得或综上：的取值范围为或