

高中数学人教A版(2019)必修第二册 空间几何体 学案
展开这是一份高中数学人教A版(2019)必修第二册 空间几何体 学案,共10页。
第十讲 立体几何体
知识点一 立体图形的直观图
学习目标
平面多边形与其直观图面积间关系:一个平面多边形的面积为S原,斜二测画法得到直观图的面积为S直,则有S直=S原.
例1 如图,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,则原图形的周长是________.
变式1、如图所示,△A′B′C′表示水平放置的△ABC用斜二测画法得到的直观图,A′B′在x′轴上,B′C′与x′轴垂直,且B′C′=3,则△ABC的边AB上的高为________.
变式2、用斜二测画法得到一水平放置的直角三角形ABC如图所示,其中AC=1,∠ABC=30°,试求原三角形A′B′C′边B′C′上的高及△A′B′C′的面积.
例2 已知等边三角形ABC的边长为a,那么等边三角形ABC的直观图△A′B′C′的面积为( )
变式1、如图所示,一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=1,那么原三角形ABO的面积是( )
变式2、如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′与x′轴垂直,且A′O′=2,则△AOB的边OB上的高为( )
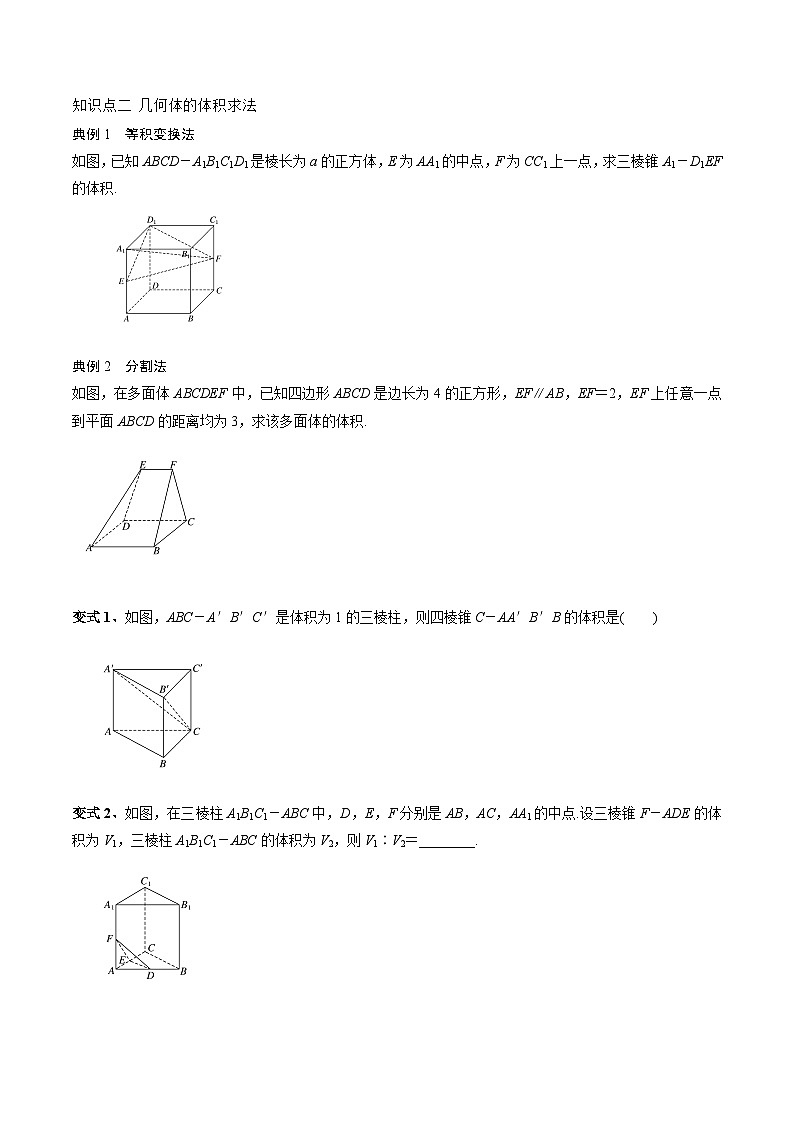
知识点二 几何体的体积求法
典例1 等积变换法
如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
典例2 分割法
如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
变式1、如图,ABC-A′B′C′是体积为1的三棱柱,则四棱锥C-AA′B′B的体积是( )
变式2、如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=________.
变式3、如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d.
变式4、如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
(1)求大棱锥、小棱锥、棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12 cm,小棱锥的底面边长为4 cm,求截得的棱台的侧面面积和表面积.
知识点三 几何体的体积和表面积公式
例1 圆锥的轴截面是等腰直角三角形,侧面积是16π,则圆锥的体积是( )
变式1 已知圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的体积为________.
例2 一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则它们的表面积之比为________.
变式1 将边长为4 cm和8 cm的矩形纸片卷成一个圆柱的侧面,则圆柱的轴截面的面积为( )
变式2 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
例3 两个球的体积之比为8∶27,那么这两个球的表面积之比为( )
变式1如图,圆柱形容器内盛有高度为6 cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )
变式2 现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.
变式3 如图在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.
知识点四 与球有关的内切、外接问题
一、直接法(公式法)
例1 (1)一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为________.
(2)一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,底面周长为3,则这个球的体积为________.
二、构造法(补形法)
1.构造正方体
例2-1 (1)一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为( )
(2)在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED,EC向上折起,使A,B重合于点P,则三棱锥P-DCE的外接球的体积为( )
2.构造长方体
例2-2 (1)若三棱锥的三个侧面两两垂直,且三条侧棱长分别为1,,,则其外接球的表面积是________.
(2)已知球O的面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=,BC= ,则球O的体积等于________.
(3)已知点A,B,C,D在同一个球面上,AB⊥平面BCD,BC⊥DC,若AB=6,AC=2,AD=8,则B,C两点间的球面距离是________.
三、寻求轴截面圆半径法
例3 正四棱锥S-ABCD的底面边长和各侧棱长都为,点S,A,B,C,D都在同一球面上,则此球的体积为________.
四、确定球心位置法
例4 已知三棱锥的四个顶点都在球O的球面上,AB⊥BC且PA=7,PB=5,PC=,AC=10,则球O的体积为________.
变式1 已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为________.
变式2 已知四面体的各面都是棱长为a的正三角形,求它外接球的体积.
1.下列命题中正确的是( )
A.两个底面平行且相似,其余各面是梯形的多面体是棱台
B.三棱柱的侧面为三角形
C.棱台的各侧棱延长后不一定交于一点
D.棱锥的侧面和底面可以都是三角形
2.(多选)下列关于圆柱的说法中正确的是( )
A.圆柱的所有母线长都相等
B.用平行于圆柱底面的平面截圆柱,截面是与底面全等的圆面
C.用一个不平行于圆柱底面的平面截圆柱,截面是一个圆面
D.一个矩形以其对边中点的连线为旋转轴,旋转180°所形成的几何体是圆柱
3.已知正方体的内切球(球与正方体的六个面都相切)的体积是π,则该正方体的体积为( )
A.4 B.16 C.8 D.64
4.一个正方体表面积与一个球表面积相等,那么它们的体积比是( )
A. B. C. D.
5.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为( )
A.5π B.6π
C.20π D.10π
6.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm,4 cm,则该棱柱的侧面积为________cm2.
7.底面为正方形的直棱柱,它的底面对角线长为,体对角线长为,则这个棱柱的侧面积是________.
8.有一个长为5 cm,宽为4 cm的矩形,则其用斜二测画法得到的直观图的面积为________cm2.
9.盛有水的圆柱形容器的内壁底面半径为5 cm,两个直径为5 cm的玻璃小球都浸没于水中,若取出这两个小球,则水面将下降多少?
10.如图,已知正三棱锥S-ABC的侧面积是底面积的2倍,正三棱锥的高SO=3,求此正三棱锥的表面积.
11.用与球心距离为2的平面去截球,所得的截面面积为π,则球的体积为( )
A. B. C.20π D.
12.长、宽、高分别为2,,的长方体的外接球的表面积为( )
A.4π B.12π C.24π D.48π
13.如图所示,半径为2的半球内有一内接正六棱锥P-ABCDEF,则该正六棱锥的体积为________.
15.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的表面积为( )
A. B.2 C. D.
16.若E,F是三棱柱ABC-A1B1C1侧棱BB1和CC1上的点,且B1E=CF,三棱柱的体积为m,求四棱锥A-BEFC的体积.
1.若五棱台ABCDEA1B1C1D1E1的表面积是30,侧面积是25,则两底面面积的和为________.
2.已知高为3的直棱柱ABCA1B1C1的底面是边长为1的正三角形,则三棱锥B1ABC的体积为________.
3.已知正五棱台的上、下底面边长分别为4 cm和6 cm,侧棱长为5 cm,则它的侧面积为________cm2.
4.如图所示,三棱锥的顶点为P,PA,PB,PC为三条侧棱,且PA,PB,PC两两互相垂直,又PA=2,PB=3,PC=4,求三棱锥PABC的体积V.
5.一个长方体的三个面的面积分别为,,,则这个长方体的体积为( )
6.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
7.棱台的体积为76 cm3,高为6 cm,一个底面面积为18 cm2,则另一个底面面积为__________.
8.直径为6的球的表面积和体积分别是( )
9.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
10.已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则该圆台较小底面的半径为( )
11.圆柱的一个底面积是S,侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
12.两个半径为1的实心铁球,熔化成一个球,这个大球的半径是________.
13.已知圆锥SO的高为4,体积为4π,则底面半径r=________.
14.若一个直立圆柱的侧视图是面积为S的正方形,则该圆柱的表面积为____________.
15.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.









