2023年中考数学专项复习测试卷——圆与正多边形

这是一份2023年中考数学专项复习测试卷——圆与正多边形，共7页。
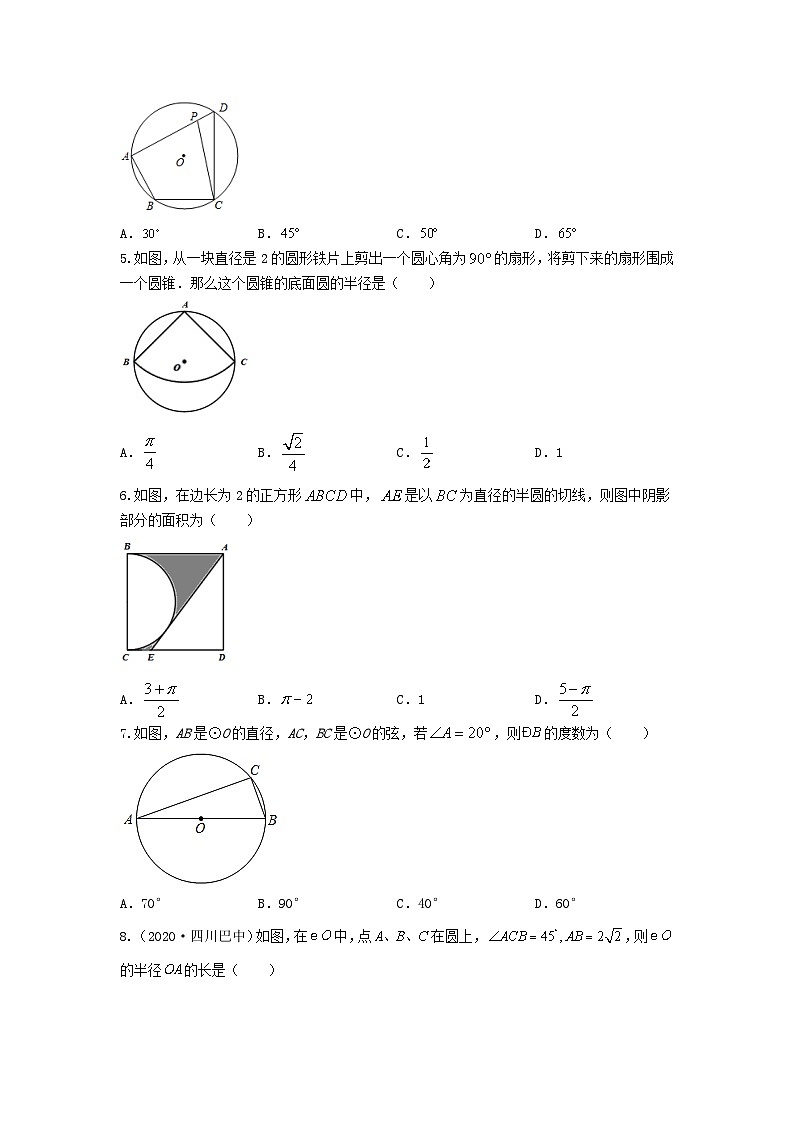
2023年中考数学专项复习测试卷——圆与正多边形（时间：60分钟      分数：100分）姓名：             班级：             学号：                分数：             第Ⅰ卷  选择题一、选择题（本题共8小题，共40分）1.（2022·贵州铜仁）如图，是的两条半径，点C在上，若，则的度数为（    ）A． B． C． D．2.如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于，两点，他测得“图上”圆的半径为10厘米，厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为（    ）A．1.0厘米/分 B．0.8厘米分 C．12厘米/分 D．1.4厘米/分3.如图，A，B，C是半径为1的⊙O上的三个点，若AB＝，∠CAB＝30°，则∠ABC的度数为（    ）A．95° B．100° C．105° D．110°4.（2021·吉林）如图，四边形内接于，点为边上任意一点（点不与点，重合）连接．若，则的度数可能为（    ）A． B． C． D．5.如图，从一块直径是2的圆形铁片上剪出一个圆心角为的扇形，将剪下来的扇形围成一个圆锥．那么这个圆锥的底面圆的半径是（    ）A． B． C． D．16.如图，在边长为2的正方形中，是以为直径的半圆的切线，则图中阴影部分的面积为（    ）A． B． C．1 D．7.如图，AB是⊙O的直径，AC，BC是⊙O的弦，若，则的度数为（    ）A．70° B．90° C．40° D．60°8.（2020·四川巴中）如图，在中，点在圆上，，则的半径的长是（    ）A． B． C． D． 第Ⅱ卷  非选择题二、填空题（本题共5小题，每空3分，共15分）9.（2022·浙江温州）若扇形的圆心角为，半径为，则它的弧长为___________．10.（2021·青海）点是非圆上一点，若点到上的点的最小距离是，最大距离是，则的半径是______．11.如图，在Rt△ABC中，∠ABC=90°，∠A=32°，点B、C在上，边AB、AC分别交于D、E两点﹐点B是的中点，则∠ABE=__________．12.（2020·黑龙江鹤岗）如图，是的外接圆的直径，若，则_____°．13.（2022·青海西宁）如图，等边三角形ABC内接于⊙O，BC=2，则图中阴影部分的面积是________．三、解答题（本题共3小题，共45分）14.（2021·山东济南）已知：如图，是的直径，，是上两点，过点的切线交的延长线于点，，连接，．（1）求证：；（2）若，，求的半径．      15.如图，A，B是上两点，且，连接OB并延长到点C，使，连接AC．（1）求证：AC是的切线．（2）点D，E分别是AC，OA的中点，DE所在直线交于点F，G，，求GF的长．      16.（2022·山东济宁）如图，在矩形ABCD中，以AB的中点O为圆心，以OA为半径作半圆，连接OD交半圆于点E，在上取点F，使，连接BF，DF．(1)求证：DF与半圆相切；(2)如果AB＝10，BF＝6，求矩形ABCD的面积．   
参考答案：1.B  2.A  3.C  4.D  5.B  6.D  7.A  8.B9.π10.或11.12.5013.14.（1）连接，如图，是的切线，，，，，，，．（2）连接是的直径，，，，，，，，，．即的半径为．15.（1）证明：∵AB=OA，OA=OB∴AB=OA=OB∴△AOB为等边三角形∴∠OAB=60°，∠OBA=60°  ∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC是⊙O的切线；（2）∵OA=4  ∴OB=AB=BC=4  ∴OC=8  ∴AC===∵D、E分别为AC、OA的中点，  ∴OE//BC，DC=过O作OM⊥DF于M，DN⊥OC于N  则四边形OMDN为矩形  ∴DN=OM在Rt△CDN中，∠C=30°，∴DN=DC=  ∴OM=连接OG，∵OM⊥GF  ∴GF=2MG=2==216.（1）证明：连接OF． ，，四边形是矩形，（2）解：连接，，，，为半圆的直径，，，，，，，在中，矩形的面积为