2020届云南省昆明市第一中学高三第七次高考仿真模拟数学（理）试题 PDF版

2020届昆一中高三联考卷第七期联考

理科数学参考答案及评分标准

命题、审题组教师   杨昆华 张宇甜 顾先成 李春宣 王海泉 莫利琴 蔺书琴 张远雄 崔锦 杨耕耘

一、选择题 

1.解析：，，所以. 选B.

2.解析：因为在复平面内对应的点位于虚轴上，所以，所以. 选A.

3.解析：该正三棱柱的左视图是边长分别为，的矩形，所以左视图的面积为，选C．

4.解析：由已知得: ，因为，选A．

5.解析：

  对，常数项为,对，，展开式中无常数项，所以的展开式中常数项为，选D.

6.解析：最短的弦为过点且与圆心和点连线垂直的弦，此时弦长为，最长的弦为直径，选D．

7.解析：函数为偶函数，排除B、C，当时，，选D.

8.解析：，选B．

9.解析：，，设是边上的中点，则，选 C.

10.解析：因为,,,所以△是直角三角形，,设为三棱锥顶点到底面的高，，，,球的体积为，选D.

11.解析:由题意知，如图，则，因为,可设,,则,,，，所以△的面积为，所以，则双曲线的焦距为，选B.

12.解析:构造函数,，易知，，可推出，，构造函数，，选B.

二、填空题

13.解析：设，则，由∥，得，由得，解方程组得：，，所以.

14.解析：直线的斜率为，故曲线在点处的切线斜率，，由导数的几何意义知，故.

15.解析: 由得：或，所以() ，而，所以，共有个零点.

16.解析:△的周长为，当且仅当P,E,F1三点共线，在射线与椭圆的交点时，△的周长最小值为，所以，所以.

三、解答题

（一）必考题

17.解析：（1）设的公比为，由得，即，

因为，解得，又，得，所以.  ………6分

（2） 

.   ………12分

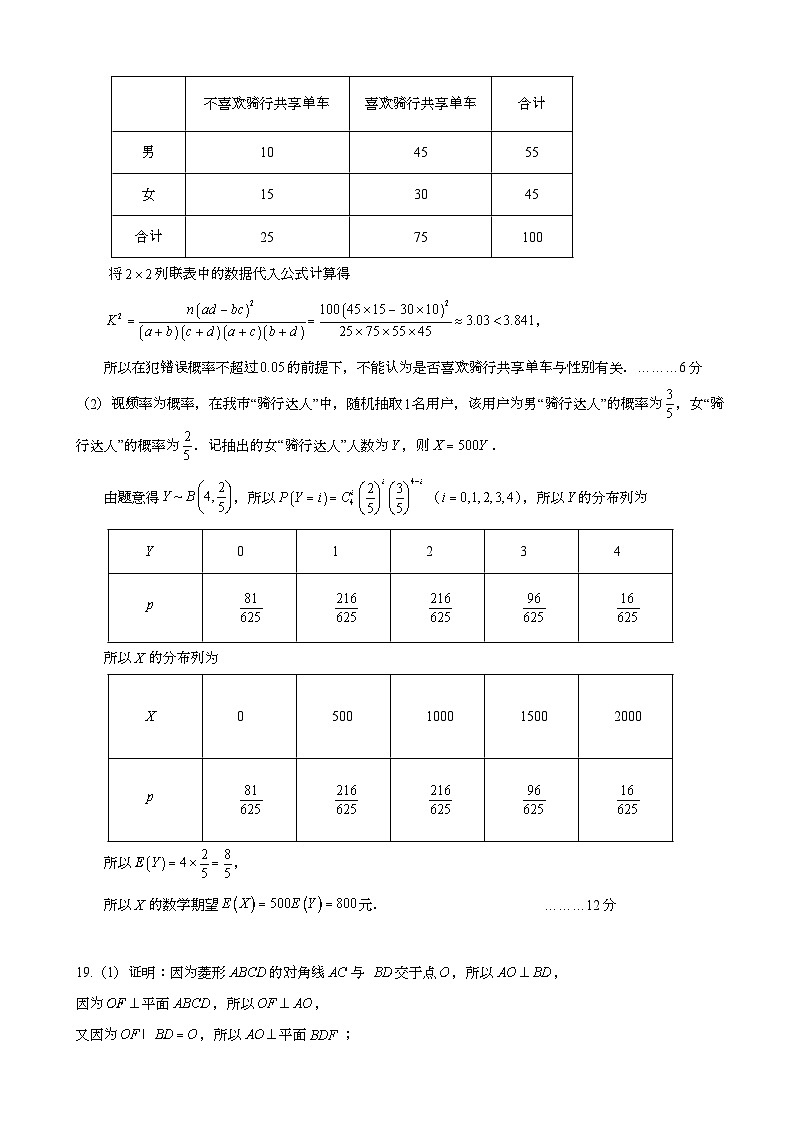
18.解：（1）由图中表格可得列联表如下：

 将列联表中的数据代入公式计算得

，

所以在犯错误概率不超过的前提下，不能认为是否喜欢骑行共享单车与性别有关．………6分                                              

（2）视频率为概率，在我市“骑行达人”中，随机抽取名用户，该用户为男“骑行达人”的概率为，女“骑行达人”的概率为．记抽出的女“骑行达人”人数为，则．

由题意得，所以（），所以的分布列为  

所以的分布列为

所以，

所以的数学期望元．                            ………12分

19.（1）证明：因为菱形的对角线与 交于点，所以，

因为平面，所以，

又因为，所以平面；

因为为线段上一点，所以，

因为四边形为平行四边形，所以∥， 

所以；                         ………5分

（2）解：设点到平面的距离为，则

，

，

因为，所以，故为线段中点；

连接，因为平面，所以，

又因为，且，所以平面，

所以，由已知得，

所以，

作，交于，则，，所以；

如图建立直角坐标系，则， ，

， ，，

 所以，，，

所以，设平面的法向量为，由

即，取，

设直线与平面所成角为，则，

即直线与平面所成角的正弦值为.                             ………12分

20.解：(1)由条件可得, ,；

设，,则，两式相减得

，

，，

所以，又，，，所以椭圆.………6分

(2)设，，当直线斜率不存在时，

，，，所以，

又，解得，.………7分

当直线斜率存在时，设直线方程为，

联立得，所以，………8分

由得，即，…………10分

原点到直线的距离为

所以

，

所以.………12分

21. 解：（1）当时，，，

若，则，则，则在单调递减；

若，则，则，则在单调递减；

故在上单调递减，又，

故当时，；当时，.                ………4分 

（2）若，当时，因为，所以，

由（1）可知，当时，，

则，与是的极小值点矛盾.

若，

设函数，则，

设函数，令，解得，因为在上单调递增，

故当时，，则，则在单调递减；

当时，，则，则在单调递增；

若，则，故当时，，则在单调递减；

当时，，则在单调递增，此时是的极小值点.

若，则，因为在单调递减，故当时，，

则，故在单调递减，与是的极小值点矛盾.

若，则，因为在单调递增，故当时，，

则，故在单调递增，与是的极小值点矛盾.

综上，当.                                                      ………12分

（二）选考题：第22、23题中任选一题做答。如果多做，则按所做的第一题记分。

22.解:（1）由直线的参数方程得：， 所以， 直线的普通方程为，斜率为2；由曲线的参数方程得：，所以，曲线的普通方程为．    ………5分

（2）联立方程组解得：，所以，以线段为直径的圆的普通方程为，化为极坐标方程得：．

                                                                           ………10分

23.解: （1）原不等式即是．

当时，由 ，解得：，所以成立；

当时, 由 ，解得：, 所以成立；

当时，由，解得：, 所以成立；

综上, 原不等式的解集为.        ………5分

（2）设，则，当 时，由 得，

且，解得， ；当 时，由 得，且，

解得，.综上， 实数的取值范围是.                  ………10分