云南省保山市2023届高三二模测数学试题（含答案）

云南省保山市2023届高三二模测数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．如果复数（其中为虚数单位，b为实数）为纯虚数，那么的模长等于（    ）

A． B．2 C．1 D．

2．定义集合运算：，设，，则集合的所有元素之和为（    ）

A．14 B．15 C．16 D．18

3．已知向量，满足，则在方向上的投影向量为（    ）

A． B． C． D．

4．足球运动是深受人们喜爱的一项体育运动，某次传球训练中，教练员让甲、乙、丙、丁4名球员进行传接球训练，从甲开始传球，等可能地传给另外3人中的1人，接球者再等可能地传给另外3人中的1人，如此一直进行.假设每个球都能被接住，若第4次传球后，球又恰好回到甲脚下，则不同的传球方法为（    ）

A．18种 B．21种 C．27种 D．45种

5．折纸艺术大约起源于公元1世纪的中国，6世纪传入日本，后经由日本传到全世界.折纸与自然科学结合在一起，不仅成为建筑学院的教具，还发展出了折纸几何学，成为现代几何学的一个分支，是一项具有艺术性的思维活动.现有一张半径为6，圆心为O的圆形纸片，在圆内选定一点P且，将圆翻折一角，使圆周正好过点P，把纸片展开，并留下一条折痕，折痕上到O，P两点距离之和最小的点为M，如此反复，就能得到越来越多的折痕，设M点的轨迹为曲线C，在C上任取一点Q，则面积的最大值是（    ）

A． B． C． D．4

6．已知正方体，Q为上底面所在平面内的动点，当直线与的所成角为45°时，点Q的轨迹为（    ）

A．圆 B．直线 C．抛物线 D．椭圆

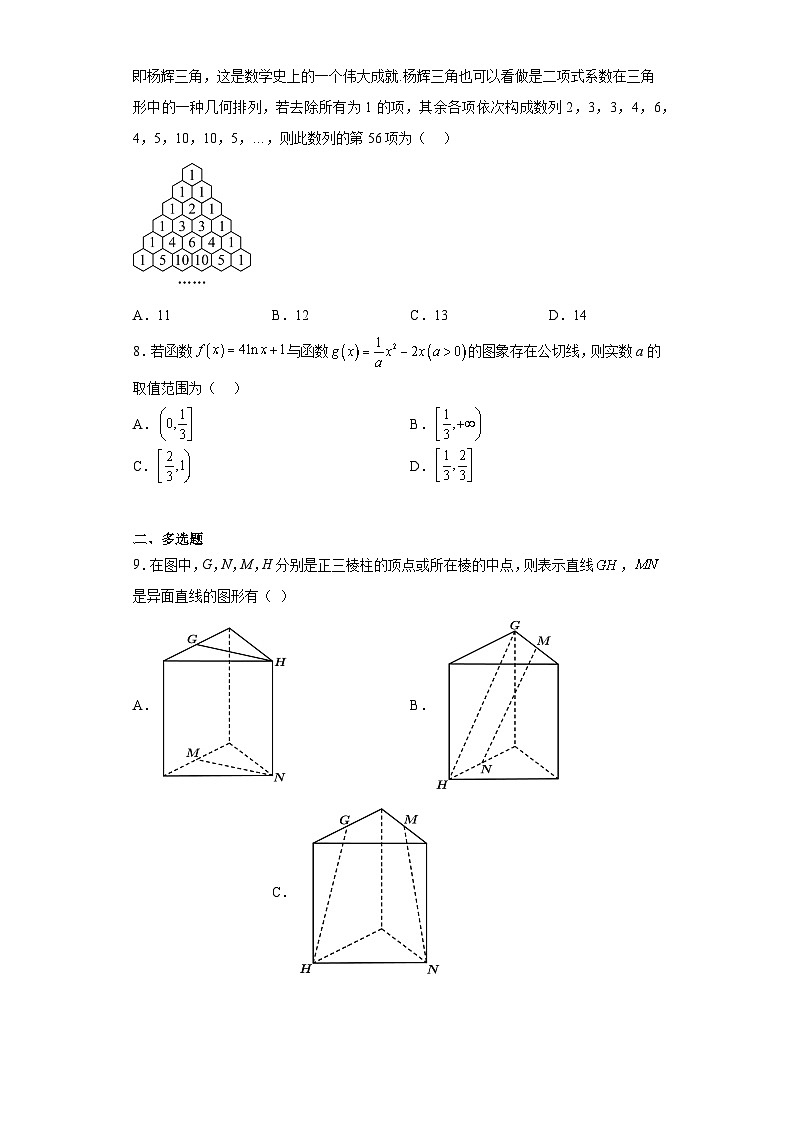
7．我国南宋数学家杨辉126l年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就.杨辉三角也可以看做是二项式系数在三角形中的一种几何排列，若去除所有为1的项，其余各项依次构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的第56项为（    ）

A．11 B．12 C．13 D．14

8．若函数与函数的图象存在公切线，则实数a的取值范围为（    ）

A． B．

C． D．

二、多选题

9．在图中，G，N，M，H分别是正三棱柱的顶点或所在棱的中点，则表示直线，是异面直线的图形有（ ）

A． B． C． D．

10．已知二项式的展开式中各项系数之和是128，则下列说法正确的有（    ）

A．展开式共有7项

B．所有二项式系数和为128

C．二项式系数最大的项是第4项

D．展开式的有理项共有4项

11．“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广，发明了“三系法”籼型杂交水稻，成功研究出“两系法”杂交水稻，创建了超级杂交稻技术体系，为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献；某杂交水稻种植研究所调查某地杂交水稻的特定时期幼苗株高，得出株高（单位：cm）服从正态分布，且的幼苗株高指标值符合优质种植标准，其中幼苗株高不低于即为合格种植标准，研究所采集了1000株互不影响生长的水稻幼苗株高样本，则下列说法正确的是（    ）

附：参考数据与公式：若，则，，.

A．幼苗株高优质种植标准约为

B．此地杂交水稻合格率约为0.97725

C．采集样本中，株高指标合格数量依然服从正态分布

D．采集样本中，株高指标合格数量最有可能是978株

12．已知函数为奇函数，的图象关于直线对称，若，则（    ）

A．函数为奇函数

B．函数的最大值是

C．函数图象关于直线对称

D．函数的最小值为

三、填空题

13．已知角的顶点为坐标原点，始边与x轴的非负半轴重合，点在角的终边上，则______.

14．春节（Spring Festival），即中国农历新年（Chinese New Year），俗称“新春”“新岁”“岁旦”等，又称“过年”“过大年”，是集除旧布新、拜神祭祖、祈福辟邪、亲朋团圆、欢庆娱乐和饮食为一体的民俗大节.某商家在春节前开展商品促销活动，凡购物顾客都可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件，若有4名顾客都领取一件礼品，其中恰有2人领取的礼品种类相同，则不同的情况共有______种.

四、双空题

15．费马点是指三角形内到三角形三个顶点距离之和最小的点，当三角形三个内角都小于时，费马点与三个顶点连线恰好三等分费马点的周角，即该点所对三角形三边的张角相等均为.根据以上性质，已知，，，M为内一点，当的值最小时，点M的坐标为_______，此时_________.

五、填空题

16．对于函数，若在其图象上存在两点关于原点对称，则称为“倒戈函数”，设函数是定义在上的“倒戈函数”，则实数m的取值范围是_______.

六、解答题

17．已知是数列的前n项和，，______.

①，；②数列为等差数列，且的前3项和为6.从以上两个条件中任选一个补充在横线处，并求解：

(1)求；

(2)设，求数列的前6项和.

注：如果选择多个条件分别解答，按第一个解答计分.

18．如图，在三棱锥中，是等边三角形，，是边的中点.

(1)求证：；

(2)，，平面与平面所成二面角为，求直线与平面所成角的余弦值.

19．中医药是包括汉族和少数民族医药在内的我国各民族医药的统称，是具有悠久历史传统和独特理论技术方法的医药体系，长期呵护着我们的健康，为中华文明的延续作出了突出贡献.某科研机构研究发现，某味中药的药用量x（单位：克）与药物功效（单位：药物功效单位）之间具有关系.

(1)估计该味中药的最佳用量与功效；

(2)对一批含有这昧中药的合成药物进行检测，发现这味中药的药用量平均值为6克，标准差为2，估计这批合成药的药物功效的平均值.

20．如图，在平面四边形中，，，.

(1)当四边形内接于圆O时，求角C；

(2)当四边形面积最大时，求对角线的长.

21．已知双曲线E：的左、右焦点分别为，，A是直线l：上不同于原点O的一个动点，斜率为的直线与双曲线E交于M，N两点，斜率为的直线与双曲线E交于P，Q两点.

(1)求的值；

(2)若直线OM，ON，OP，OQ的斜率分别为，，，，问是否存在点A，满足+++=0，若存在，求出A点坐标；若不存在，说明理由.

22．设函数，

(1)求在区间上的极值点个数；

(2)若为的极值点，则，求整数的最大值.

参考答案：

1．A

2．A

3．D

4．B

5．B

6．C

7．B

8．A

9．BD

10．BD

11．ABD

12．BC

13．/

14．36

15．         

16．

17．(1)

(2)

18．(1)证明见解析

(2).

19．(1)该药物使用量为克时可达最大功效.

(2)

20．(1)

(2).

21．(1)

(2)存在，或

22．(1)

(2)