2023届高考数学二轮复习微专题42线性约束条件下的非线性目标函数取值范围问题学案

这是一份2023届高考数学二轮复习微专题42线性约束条件下的非线性目标函数取值范围问题学案，共7页。


例题1(2018·扬州一模)若实数x，y满足eq \b\lc\{(\a\vs4\al\c1(x≤4，,y≤3，,3x＋4y≥12，))则x2＋y2的取值范围是________________．
例题2(2018·苏锡常镇一模)若二次函数f(x)＝ax2＋bx＋c(a>0)在区间[1，2]上有两个不同的零点，则eq \f(f（1）,a)的取值范围为________________．
变式1若实数a，b，c，d满足eq \f(a2－2lna,b)＝eq \f(3c－4,d)＝1，则(a－c)2＋(b－d)2的最小值是________________．
变式2若关于x的方程x2－(a2＋b2－6b)x＋a2＋b2＋2a－4b＋1＝0的两根x1，x2满足x1≤0≤x2≤1，则a2＋b2＋4a的取值范围为________________．
串讲1已知实数x，y满足不等式|x|＋|y|≤1，则z＝eq \f(y－2,x－2)的最大值为________________．
串讲2已知P(x，y)的坐标满足eq \b\lc\{(\a\vs4\al\c1(\r(3)x－y＜0，,x－\r(3)y＋2＜0，,y≥0，))则eq \f(\r(3)x＋y,2\r(x2＋y2))的取值范围为________________．
已知实数x，y满足约束条件eq \b\lc\{(\a\vs4\al\c1(x－y≤0，,x＋y－5≥0，,y－3≤0，))若不等式m(x2＋y2)≤(x＋y)2恒成立，则实数m的最大值是________________．
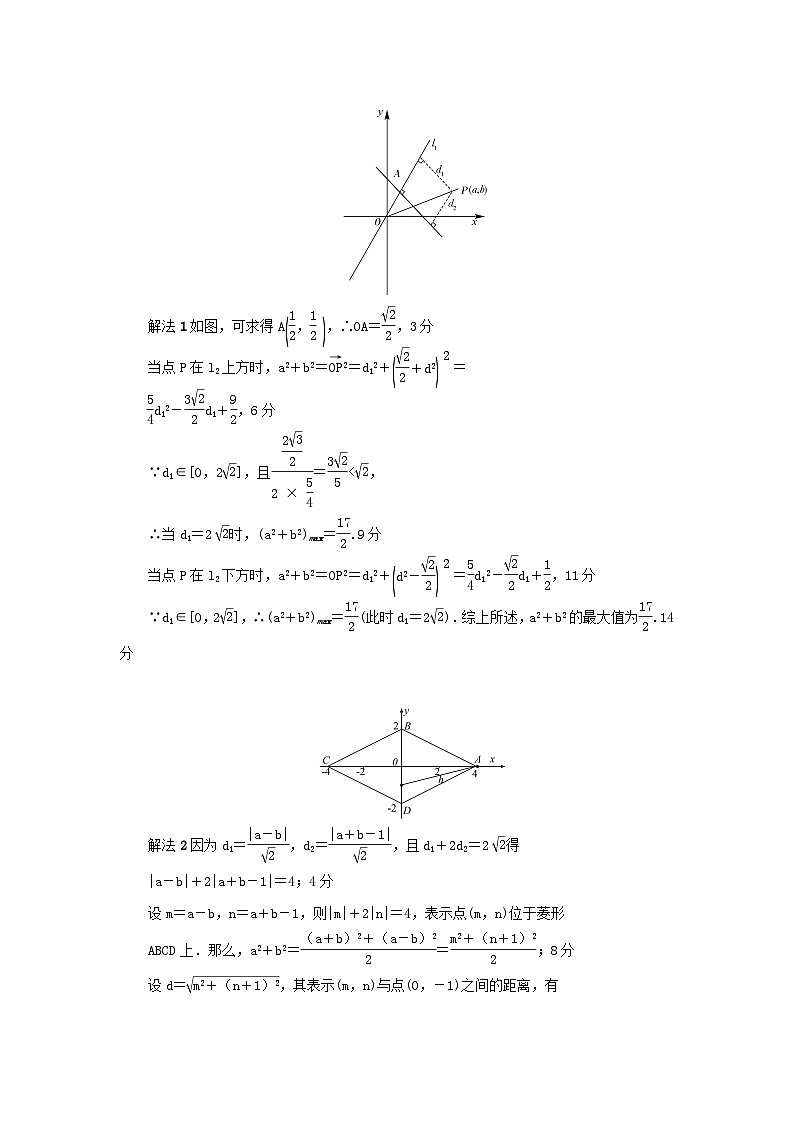
在平面直角坐标系xOy中，若动点P(a，b)到直线l1：y＝x，l2：y＝－x＋1的距离分别为d1，d2，且满足d1＋2d2＝2eq \r(2)，求a2＋b2的最大值为________．
答案：eq \f(17,2).
解法1如图，可求得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，\f(1,2)))，∴OA＝eq \f(\r(2),2)，3分
当点P在l2上方时，a2＋b2＝eq \(OP,\s\up6(→))2＝d12＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)＋d2))eq \s\up12(2)＝
eq \f(5,4)d12－eq \f(3\r(2),2)d1＋eq \f(9,2)，6分
∵d1∈[0，2eq \r(2)]，且eq \f(\f(2\r(3),2),2×\f(5,4))＝eq \f(3\r(2),5)∴当d1＝2eq \r(2)时，(a2＋b2)max＝eq \f(17,2).9分
当点P在l2下方时，a2＋b2＝OP2＝d12＋eq \b\lc\(\rc\)(\a\vs4\al\c1(d2－\f(\r(2),2)))eq \s\up12(2)＝eq \f(5,4)d12－eq \f(\r(2),2)d1＋eq \f(1,2)，11分
∵d1∈[0，2eq \r(2)]，∴(a2＋b2)max＝eq \f(17,2)(此时d1＝2eq \r(2))．综上所述，a2＋b2的最大值为eq \f(17,2).14分
解法2因为d1＝eq \f(|a－b|,\r(2))，d2＝eq \f(|a＋b－1|,\r(2))，且d1＋2d2＝2eq \r(2)得
|a－b|＋2|a＋b－1|＝4；4分
设m＝a－b，n＝a＋b－1，则|m|＋2|n|＝4，表示点(m，n)位于菱形
ABCD上．那么，a2＋b2＝eq \f(（a＋b）2＋（a－b）2,2)＝eq \f(m2＋（n＋1）2,2)；8分
设d＝eq \r(m2＋（n＋1）2)，其表示(m，n)与点(0，－1)之间的距离，有
dmax＝eq \r(17)，得到a2＋b2≤eq \f(d2,2)＝eq \f(17,2).14分
微专题42
例题1
答案：[eq \f(144,25)，25]．
解析：设x2＋y2＝r2，由图形可知r2∈[eq \f(144,25)，25]．
例题2
答案：[0，1)．
解法1设函数f(x)的零点为x1，x2(1≤x1解法2设由题意可知
eq \b\lc\{(\a\vs4\al\c1(f（1）≥0，,f（2）≥0，,Δ＝b2－4ac>0，,1<－\f(b,2a)<2，))
即eq \b\lc\{(\a\vs4\al\c1(a＋b＋c≥0，,4a＋2b＋c≥0，,b2－4ac>0，,1<－\f(b,2a)<2.))又eq \f(f（1）,a)＝eq \f(a＋b＋c,a)＝1＋eq \f(b,a)＋eq \f(c,a)，设x＝eq \f(b,a)，y＝eq \f(c,a)，则
eq \b\lc\{(\a\vs4\al\c1(x2>4y，,x＋y＋1≥0，,2x＋y＋4≥0，,－4说明：作图时要注意到两直线和抛物线都相切！
变式联想
变式1
答案：eq \f(2（ln 2－1）2,5).
解析：令(a－c)2＋(b－d)2＝r2，则r＝eq \r(（a－c）2＋（b－d）2)表示点(a，b)，(c，d)之间的距离；即直线d＝3c－4上的点到曲线a2－2lna＝b上的点的距离．
只要求直线d＝3c－4的平行线与曲线a2－2lna＝b的切点，即2a－eq \f(2,a)＝3，得a＝2或－eq \f(1,2)(舍去)．
那么，即要求(2，4－2ln2)到直线的距离，rmin＝eq \f(2|ln2－1|,\r(10))，亦即(a－c)2＋(b－d)2的最小值为eq \f(2（ln2－1）2,5).
变式2
答案：eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(7,2)，5＋4\r(5))).
解析：设f(x)＝x2－(a2＋b2－6b)x＋a2＋b2＋2a－4b＋1，则由题意可知eq \b\lc\{(\a\vs4\al\c1(f（0）≤0，,f（1）≥0，))
即eq \b\lc\{(\a\vs4\al\c1(（a＋1）2＋（b－2）2≤4，,a＋b＋1≥0，))作出可行域如图，则
eq \r(（a＋2）2＋b2)∈
eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(2),2)，2＋\r(5)))；又a2＋b2＋4a＝(a＋2)2＋b2－4∈[－eq \f(7,2)，
5＋4eq \r(5)]．
串讲激活
串讲1
答案：2.
解析：|x|＋|y|≤1表示的平面区域为正方形ABCD内部及其边界，设P(2，2)，由图可知z的最大值为kPA.易知kPA＝eq \f(2－0,2－1)＝2.
串讲2
答案：eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，\f(\r(3),2))).
解析：eq \f(\r(3)x＋y,2\r(x2＋y2))
＝eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)，\f(1,2)))·（x，y）,|（x，y）|)＝csθ；其中θ为向量eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)，\f(1,2)))与向量(x，y)的夹角，由可行域可知
θ∈eq \b\lc\(\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3)))，
那么，csθ∈eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，\f(\r(3),2))).
新题在线
答案：eq \f(25,13).
解析：作出线性约束条件下的可行域如图中阴影部分所示，显然，
A(2，3)，B(3，3)．令目标函数z＝eq \f(y,x)，它表示经过点(0，0)及可行域内的点(x，y)的直线的斜率，从
而1≤z≤eq \f(3,2).不等式m(x2＋y2)≤(x＋y)2恒成立，也就是m≤eq \f(（x＋y）2,x2＋y2)恒成立，
令u＝eq \f(（x＋y）2,x2＋y2)，则u＝1＋
eq \f(2xy,x2＋y2)＝1＋eq \f(2,\f(y,x)＋\f(x,y))＝
非线性目标函数在线性约束条件下的最值问题是经典考点，在解题时，尤其要注意对目标函数的几何意义(如距离、斜率、面积等)进行仔细分析，通过可行域进行分析代数结构，感悟数形转化的思想.