中考训练高频考点专题：反比例函数与一次函数的综合专项训练与解析

高频考点专题：反比例函数与一次函数的综合

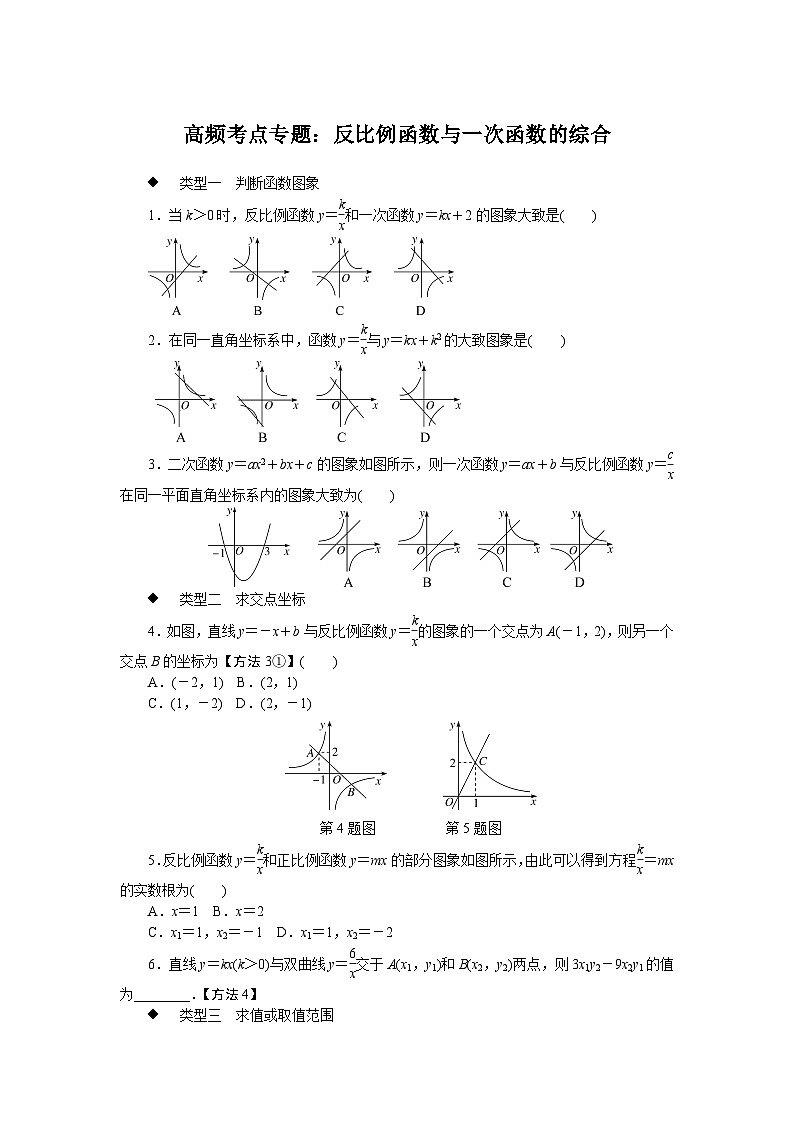
类型一　判断函数图象

1．当k＞0时，反比例函数y＝和一次函数y＝kx＋2的图象大致是(　　)

2．在同一直角坐标系中，函数y＝与y＝kx＋k2的大致图象是(　　)

3．二次函数y＝ax2＋bx＋c的图象如图所示，则一次函数y＝ax＋b与反比例函数y＝在同一平面直角坐标系内的图象大致为(　　)

类型二　求交点坐标

4．如图，直线y＝－x＋b与反比例函数y＝的图象的一个交点为A(－1，2)，则另一个交点B的坐标为【方法3①】(　　)

A．(－2，1)  B．(2，1)

C．(1，－2)  D．(2，－1)

第4题图          第5题图

5．反比例函数y＝和正比例函数y＝mx的部分图象如图所示，由此可以得到方程＝mx的实数根为(　　)

A．x＝1  B．x＝2

C．x1＝1，x2＝－1  D．x1＝1，x2＝－2

6．直线y＝kx(k＞0)与双曲线y＝交于A(x1，y1)和B(x2，y2)两点，则3x1y2－9x2y1的值为________．【方法4】

类型三　求值或取值范围

7．已知一次函数y1＝ax＋b与反比例函数y2＝的图象如图所示，当y1＜y2时，x的取值范围是【方法3③】(　　)

A．x<2   B．x>5   C．0<x<5   D．0<x<2或x>5

第7题图          第8题图

8．如图，正比例函数y1＝k1x(k1≠0)的图象与反比例函数y2＝(k2≠0)的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是【方法3③】(　　)

A．x＜－2或x＞2          B．x＜－2或0＜x＜2

C．－2＜x＜0或0＜x＜2    D．－2＜x＜0或x＞2

9．若一次函数y＝mx＋6与反比例函数y＝的图象在第一象限有公共点，则有(　　)

A．mn≥－9  B．－9≤mn≤0   C．mn≥－4  D．－4≤mn≤0

10．如图，点M是函数y＝x与y＝的图象在第一象限内的交点，OM＝4，则k的值为________．

第10题图               第11题图

11．如图，过C(2，1)作AC∥x轴，BC∥y轴，点A，B都在直线y＝－x＋6上．若双曲线y＝(x＞0)与△ABC总有公共点，则k的取值范围是____________．

12．如图，一次函数y＝x＋m的图象与反比例函数y＝的图象交于A，B两点，且与x轴交于点C，点A的坐标为(2，1)．

(1)求m及k的值；

(2)求点C的坐标，并结合图象写出不等式组0＜x＋m≤的解集．

13．如图，反比例函数y＝与一次函数y＝ax＋b的图象交于点A(2，2)，B.

(1)求这两个函数的解析式；

(2)将一次函数y＝ax＋b的图象沿y轴向下平移m个单位，使平移后的图象与反比例函数y＝的图象有且只有一个交点，求m的值．

14．如图，直线y＝x＋3与y轴交于点A，与x轴交于点C，直线l1与y轴交于点A，与x轴交于点B，且两直线互相垂直．

(1)点A的坐标为________，点B的坐标为________，点C的坐标为________；

(2)已知双曲线y＝－与l1的交点坐标为(－1，k)，求k的值；

(3)请利用图象直接写出不等式－>x＋3的解集．

类型四　求图形的面积

15．如图，已知某一次函数与反比例函数的图象相交于A(1，3)，B(m，1)，求：

(1)m的值与一次函数的解析式；

(2)△ABO的面积．

参考答案与解析

1．C　2.C　3.B　4.D　5.C

6．36　解析：由题可知点A(x1，y1)，B(x2，y2)关于原点对称，∴x1＝－x2，y1＝－y2.把A(x1，y1)代入y＝，得x1y1＝6，∴3x1y2－9x2y1＝－3x1y1＋9x1y1＝6x1y1＝36.

7．D　8.D

9．A　解析：将y＝mx＋6代入y＝中，得mx＋6＝，整理得mx2＋6x－n＝0.∵两个图象有公共点，∴Δ＝62＋4mn≥0，∴mn≥－9.故选A.

10．4

11．2≤k≤9　解析：当反比例函数的图象过C点时，把C的坐标代入得k＝2×1＝2.把y＝－x＋6代入y＝得－x＋6＝，整理得x2－6x＋k＝0，Δ＝(－6)2－4k＝36－4k.∵反比例函数y＝的图象与△ABC有公共点，∴36－4k≥0，解得k≤9，∴k的取值范围是2≤k≤9.

12．解：(1)∵点A(2，1)在一次函数y＝x＋m的图象上，∴2＋m＝1，∴m＝－1.∵点A(2，1)在反比例函数y＝的图象上，∴＝1，∴k＝2.

(2)由(1)可知m＝－1，∴一次函数的解析式为y＝x－1，令y＝0，得x＝1，∴点C的坐标是(1，0)．由图象可知不等式组0＜x＋m≤的解集为1＜x≤2.

13．解：(1)∵A(2，2)在反比例函数y＝的图象上，∴k＝4，∴反比例函数的解析式为y＝.∵点B在反比例函数y＝的图象上，∴n＝4，解得n＝8，∴点B的坐标为.由A(2，2)，B在一次函数y＝ax＋b的图象上，得解得∴一次函数的解析式为y＝－4x＋10.

(2)由(1)可知反比例函数的解析式为y＝，一次函数的解析式为y＝－4x＋10，它的图象沿y轴向下平移m个单位得到的直线的解析式为y＝－4x＋10－m.令－4x＋10－m＝，得4x2＋(m－10)x＋4＝0.∵直线y＝－4x＋10－m与双曲线y＝有且只有一个交点，∴Δ＝(m－10)2－64＝0，解得m＝2或m＝18.

14．解：(1)(0，3)　(1.5，0)　(－6，0)

(2)设l1的解析式为y＝k1x＋3，由题意可得k1＝－2，∴y＝－2x＋3.∵双曲线y＝－与l1的交点坐标为(－1，k)，∴－2×(－1)＋3＝k，∴k＝5.

(3)从图象上看，双曲线y＝－与直线y＝x＋3没有交点，且与x<0时，双曲线y＝－在直线y＝x＋3的上方，∴不等式－>x＋3的解集是x<0.

15．解：(1)设一次函数与反比例函数的解析式分别为y＝ax＋b，y＝.将A(1，3)，B(m，1)代入y＝中，得解得∴点B的坐标为(3，1)．将A(1，3)，B(3，1)代入y＝ax＋b中，得解得∴一次函数的解析式为y＝－x＋4.

(2)设一次函数y＝－x＋4的图象交x轴于点C，∴点C的坐标为(4，0)，∴OC＝4.∵A(1，3)，B(3，1)，∴S△AOB＝S△AOC－S△BOC＝×4×(3－1)＝4.