2023年河北省邯郸市育华中学中考三模数学试卷(含答案)

2023.5.13育华初三三模数学试卷

数学

一、选择题（本大题共16个小题。1~10小题每题3分，11~16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.以下选项是最简二次根式的是（    ）

A. B. C. D.

2.下列计算正确的是（    ）

A. B. C. D.

3.表示a是非负数的是（    ）

A. B. C. D.

4.如图，把三角形ABC沿BC方向平移1个单位长度得到三角形DEF，若四边形ABFD的周长为10，则三角形ABC的周长为（    ）

A.8 B.10 C.12 D.14

5.观察下列尺规作图的痕迹，不能判断是等腰三角形的是（    ）.

A. B. C. D.

6.正方形周长是160000，它的边长用科学记数法表示应为（    ）

A. B. C. D.

7.已知点M在第四象限，且到x轴的距离为2，到y轴的距离为4，则M的坐标为（    ）

A. B. C. D.

8.如图，球在灯泡的照射下形成了影子，当球竖直向下运动时，球的影子的大小变化是（    ）

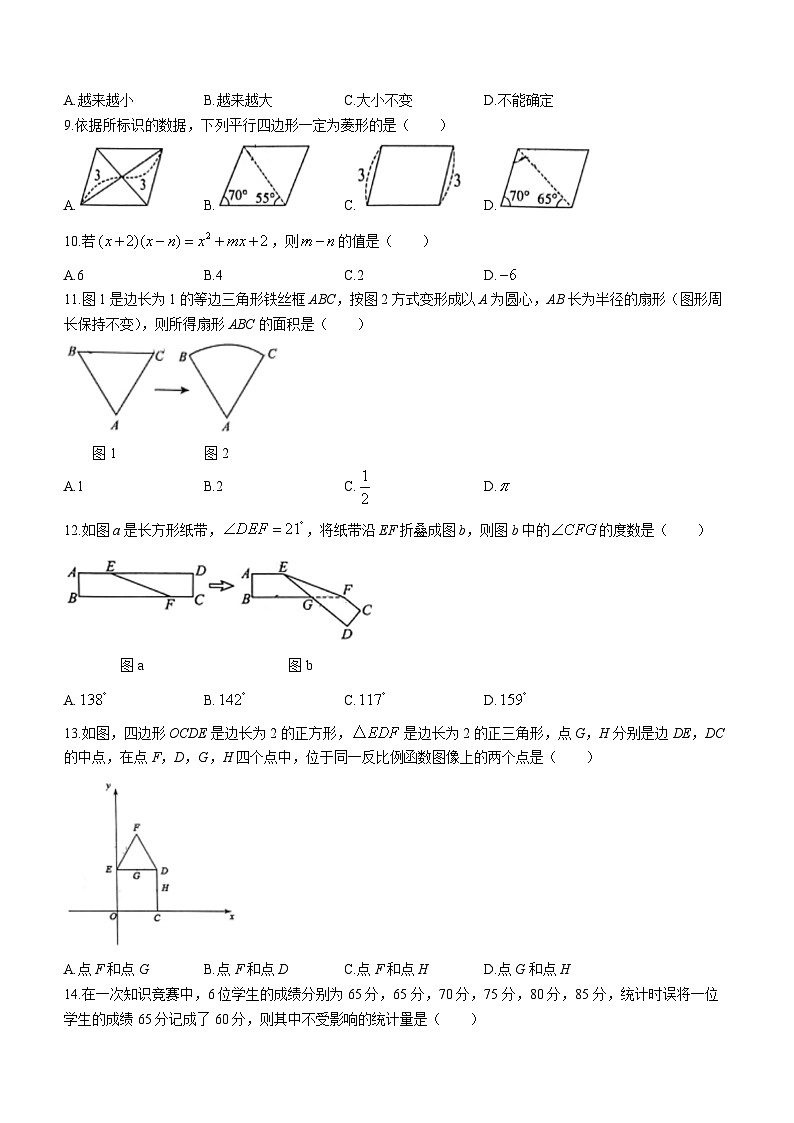
A.越来越小 B.越来越大 C.大小不变 D.不能确定

9.依据所标识的数据，下列平行四边形一定为菱形的是（    ）

A. B. C. D.

10.若，则的值是（    ）

A.6 B.4 C.2 D.

11.图1是边长为1的等边三角形铁丝框ABC，按图2方式变形成以A为圆心，AB长为半径的扇形（图形周长保持不变），则所得扇形ABC的面积是（    ）

图1    图2

A.1 B.2 C. D.

12.如图a是长方形纸带，，将纸带沿EF折叠成图b，则图b中的的度数是（    ）

图a      图b

A. B. C. D.

13.如图，四边形OCDE是边长为2的正方形，是边长为2的正三角形，点G，H分别是边DE，DC的中点，在点F，D，G，H四个点中，位于同一反比例函数图像上的两个点是（    ）

A.点F和点G B.点F和点D C.点F和点H D.点G和点H

14.在一次知识竞赛中，6位学生的成绩分别为65分，65分，70分，75分，80分，85分，统计时误将一位学生的成绩65分记成了60分，则其中不受影响的统计量是（    ）

A.平均数 B.中位数 C.众数 D.方差

15.如图，铅笔放置在的边AB上，笔尖方向为点A到点B的方向，把铅笔依次绕点A、点C、点B按逆时针方向旋转、、的度数后，笔尖方向变为点B到点A的方向，这种变化说明（    ）

图1    图2   图3    图4

A.三角形任意两边之和大于第三边

B.三角形外角和等于

C.三角形内角和等于

D.三角形任意两边之差小于第三边

16.九年级某班计划在劳动实践基地内种植蔬菜，班长买回来8米长的围栏，准备围成一边靠墙（墙足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰直角三角形（底边靠墙）、半圆形这三种方案，如图所示，最佳方案是（    ）

方案1   方案2   方案3

A.方案1 B.方案2 C.方案3 D.面积都一样

二、填空题（本大题有3个小题，共10分.17~18小题各3分；19小题有2个空，每空2分）

17.在一个不透明的盒子中装有6张形状、大小、质地均相同的卡片，上面分别标有数字1，2，3，4，5，6.从中随机同时抽取1张卡片，那么抽取的卡片上的数字是3的概率是______.

18.如图，在正方形网格中，每个小正方形的边长都是1，是的外接圆，点A，B，O在网格线的交点上，则的值是______.

19.已知两个正数a，b，可按规则扩充为一个新数c.在a，b，c三个数中取两个较大的数，按上述规则扩充得到一个新数，依此继续扩充下去，将每扩充一次得到一个新数称为一次操作，

（1）若，，按上述规则操作三次，扩充所得的数是______；

（2）若，按上述规则操作五次后扩充所得的数为（m，n为正整数），则______.

三、解答题（共68分）

20.如图，点A，B均在数轴上，点B在点A的右侧，点A对应的数字是，点B对应的数字是m.

（1）若，求m的值；

（2）点C是线段AB上一点且，点C对应的数字是n，若，求m的值.

21.为了解某校九年级学生的理化生实验操作情况，随机抽查了若干名学生的实验操作得分（满分为10分），根据获取的样本数据，制作了如图的统计图（1）和图（2），图中的一部分被纸片挡住了，请根据相关信息，解答下列问题：

图（1）     图（2）

（1）本次随机抽查的学生人数为______，在图（2）中，“①”的描述应为“7分m%”，其中m的值为______.

（2）计算抽取的学生实验操作得分数据的平均数.

（3）若该校九年级共有1280名学生，估计该校理化生实验操作得满分的学生有多少人?

22.如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”.如，，.因此，4、12、20这三个数都是神秘数.

（1）验证28和44这两个数是否为神秘数。

（2）设两个连续偶数为和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗?请推演你的结论。

23.如图，灌溉车为绿化带浇水，喷水口H离地竖直高度OH为1.5m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图像；把绿化带横截面抽象为矩形DEFG，其水平宽度，竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到，上边抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到绿化带的距离OD为d（单位：m）.

（1）求上边缘抛物线的函数解析式，并求喷出水的最大射程OC；

（2）通过计算说明点B到点H的距离和点B到点A的距离哪个更长；

（3）要使灌溉车行驶时喷出的水能浇灌到整个绿化带，直接写出d的取值范围.

24.如图1所示的圆弧形混凝上管片是构成圆形隧道的重要部件.管片的横截面（阴影部分）如图2所示，是同心圆环的一部分，左右两边沿的延长线交于圆心，甲、乙、丙三个小组分别采用三种不同的方法，测算三片不同大小的混凝土管片的外圆弧半径.

图1    图2    图3      图4

（1）如图2，BA，CD的延长线交于圆心O，若甲组测得，，，求OB的长.

（2）如图3，ED，FC的延长线交于圆心H，若乙组测得，，，直接写出EH的长.

（3）如图4，有一混凝土管片放置在水平地面上，底部用两个完全相同的长方体木块固定，管片与地面的接触点L为的中点，若丙组测得，，求该管片的外圆弧半径.

25.数学兴趣小组探究平面内横、纵坐标满足特定关系的动点的运动轨迹问题：

（1）组长提出问题：动点随着t的变化形成的运动轨迹是什么?

甲同学的思考：t取3个特殊值得到3个点坐标，发现3点在一条直线上，可以利用待定系数法求出该直线的表达式；乙同学的思考：令，，通过消去t得到y与x的函数关系式.

______（填甲或乙）同学的方法更严谨，点运动轨迹的函数表达式为______；

（2）如图，在平面直角坐标系中，已知点，，Q为坐标系内一点且，点M从点A出发以每秒8个单位的速度沿x轴向左运动，同时点N从点O出发以每秒6个单位的速度沿y轴向上运动，点P是MN的中点，设运动时间为t.求点P的运动轨迹的函数表达式，并计算当时PQ的最小值；

（3）老师给出坐标平面内两个动点：，.

丙学说：点T、K的运动轨迹都是直线；丁同学说：点T、K在运动过程中不可能重合；请你判断两人结论是否正确并说明理由。

26.（1）如图①，在正方形ABCD中，，点F，G分别在AB，CD上，连接FG，若，，以FG为斜边，向下作直角三角形EFG，则在边BC上存在______个符合条件的直角顶点E；

（2）在（1）的条件下，若存在符合条件的，求的面积，若不存在，求FG的长；

（3）某小区有一个边长为40米的正方形ABCD活动区域，小区物业在一面墙BC的中点E处安装一台监控器，该监控器的视角为，监控器可以左右来回转动，并且可以监控该区域的每一个地方，如图②，，与正方形ABCD内，连接FG，若G在线段AD上运动时，请计算面积的最值；

（4）在（3）的条件下，若G在线段CD上运动时（不含C、D两点），请直接写出的值.

图①    备用图    图②

2023.5.13育华三模数学答案

一、CADAD DBABB CADBCC

二、17. 18.2  19.255 13